ПОШАГОВОЕ ОПИСАНИЕ АЛГОРИТМА КЛАРКА_РАЙТА
ОПИСАНИЕ ПОСЛЕДОВАТЕЛЬНОГО РЕШЕНИЯ МЕТОДОМ КЛАРКА_РАЙТА
ВВЕДЕНИЕ.
Описанный метод используется в программе "Простое формирование маршрутов. Работа с картой. Расчет оптимальных вариантов доставки"
В статье "Оптимизация планирования доставки грузов. Алгоритм кластеризации k-means (метод K-средних)" было показано, КАК ПОЛУЧИТЬ ОПТИМАЛЬНЫЕ МАРШРУТЫ ДЛЯ ЗАДАННОГО КОЛИЧЕСТВА А/ТРАНСПОРТА из указанного места отгрузки, при этом грузоподъемность транспорта не принималась во внимание .
В этой статье покажем КАК УЗНАТЬ КОЛИЧЕСТВО НЕОБХОДИМОГО А/ТРАНСПОРТА С УЧЕТОМ ЕГО ГРУЗОПОДЪЕМНОСТИ ДЛЯ ФОРМИРОВАНИЯ ОПТИМАЛЬНЫХ МАРШРУТОВ.
Итак, поставлена задача отыскать самый выгодный маршрут движения транспорта, проходящий по одному разу через указанные пункты с последующим возвратом в исходный пункт (база). Критериями оптимальности в данной постановке задачи являются: минимальный пробег транспортного средства при максимальной загрузке кузова.
Сформулированная задача известна как «задача коммивояжера». Существует множество математических методов, позволяющих найти как точное, так и приближенное решение поставленной задачи. Среди методов, дающих точное решение, наиболее известны:
- «полный перебор»
- «метод ветвей и границ»
Основным недостатком данных методов является высокая временная и емкостная сложность, что важно учитывать при большом количестве пунктов. Все эффективные (сокращающие полный перебор) методы решения «задачи коммивояжера» – методы эвристические. Из них наибольшее применение нашли:
- «метод генетических алгоритмов»
- «метод Кларка-Райта»
- «алгоритм муравьиной колонии»
- «метод ближайшего соседа»
- «метод включения ближайшего города»
- «метод самого дешевого включения»
Для решения нашей задачи наиболее приемлемым методом является метод Кларка-Райта. Он относится к числу приближенных, итерационных методов и может использоваться для компьютерного решения задачи развозки. Погрешность решения не превосходит в среднем 5–10 %. Достоинствами метода являются его простота, надежность и гибкость, что позволяет учитывать целый ряд дополнительных факторов, влияющих на конечное решение задачи.
Рассмотрим на примере, как применять метод Кларка-Райта.
ПОСТАНОВКА ЗАДАЧИ.
Из исходного пункта, в котором располагается грузовой терминал (склад), необходимо доставить грузы 12 получателям.
Таблица 1. Координаты и объем спроса получателей
Координаты грузового терминала (склада): x0 = 10, y0 = 15. Для доставки будет использоваться транспорт с максимальной грузовместимостью = 1500 шт.
ВОПРОС: Какое количество транспорта понадобится для развозки грузов ? Какая схема развозки будет оптимальной ?
ПОДГОТОВИТЕЛЬНАЯ РАБОТА.
Отметим эти точки в декартовой системе координат. Местоположение оптовой базы и 12 получателей, а также объем поставок каждому получателю приведены на рисунке 1.
Рисунок 1. Расположение базы и пунктов доставки
Начальная схема маршрутов предполагает что для доставки груза каждому отдельному получателю организуется отдельный маршрут (см. рис. 2). Например, водитель загружает в кузов партию 450 шт. и везет ее в пункт 1, там разгружается, затем возвращается на базу, берет вторую партию 400 шт. и везет ее в пункт 2 и т.д. Таким образом, исходная схема развозки включает в себя только радиальные маршруты движения автомобиля, причем количество радиальных маршрутов совпадает с количеством получателей. В данном случае, схема развозки состоит из 12 радиальных маршрутов.
Рисунок 2. Начальная схема доставки груза
Суть метода заключается в том, чтобы, отталкиваясь от исходной схемы развозки, по шагам перейти к оптимальной схеме развозки с кольцевыми маршрутами. С этой целью вводится такое понятие, как километровый выигрыш.
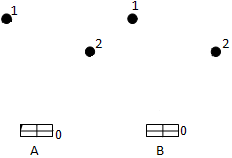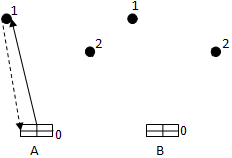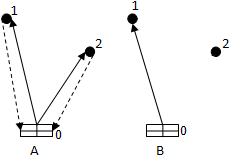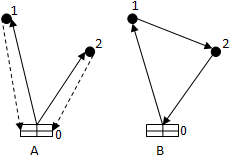
Рисунок 3. Схемы доставки
На рисунке 3. отображены две схемы доставки. Схема доставки А (слева) обеспечивает доставку грузов в пункты 1 и 2 по радиальным маршрутам. В этом случае суммарный пробег автотранспорта равен:
La = d01 + d10 + d02 + d20 = 2d01 + 2d02
Схема доставки B предполагает доставку грузов в пункты 1 и 2 по кольцевому маршруту. Тогда пробег автотранспорта составляет:
Lв = d01 + d12 + d02
Схема В по показателю пробега автотранспорта дает, как правило, лучший результат, чем схема А. И поэтому при переходе от схемы А к схеме В получаем следующий километровый выигрыш:
S12 = La - Lв = d01 + d02 - d12
В общем случае мы имеем километровый выигрыш:
Sij = d0i + d0j - dij
где Sij – километровый выигрыш, получаемый при объединении пунктов i и j, км; d0i, d0j – расстояние между оптовой базой и пунктами i и j соответственно, км; dij – расстояние между пунктами i и j, км.
Полученные значения заносятся в таблицу 2., где представлены расстояния между пунктами dij (правая верхняя часть матрицы) и километровые выигрыши Sij (левая нижняя часть матрицы).
Таблица 2. Матрица расстояний и километровых выигрышей
Теперь вернемся к нашему примеру. Из табл. 1 возьмем данные:
- Пункт 0 (это база): x0 = 10, y0 = 15
- Пункт 1: х1 = 17, у1 = 15
- Пункт 2: х2 = 6, у2 = 15
- Пункт 3: x3 = 13, y3 = 3
- и т.д.
Рассчитаем расстояние d01 между пунктами 0 и 1 по формуле:
Аналогично получаем расстояние:
- для пунктов 0 и 2: d02 = 4
- для пунктов 0 и 3: d03 = 12,37
- для пунктов 1 и 2: d12 = 11
- для пунктов 1 и 3: d13 = 12,65
- для пунктов 2 и 3: d23 = 13,89
- и т.д
Потом для пунктов i и j получаем километровый выигрыш Sij = d0i + d0j - dij:
- для пунктов 1 и 2: S12 = d01 + d02 - d12 = 7 + 4 - 11 = 0
- для пунктов 1 и 3: S13 = d01 + d03 - d13 = 7 + 12.37 - 12.65 = 6.72
- для пунктов 2 и 3: S13 = d02 + d03 - d23 = 4 + 12.37 - 13.89 = 2.48
- и т.д.
Полученные значения заносим в таблицу 3., где представлены расстояния между пунктами dij (правая верхняя часть матрицы) и километровые выигрыши sij (левая нижняя часть матрицы):
Таблица 3. Расчетная матрица расстояний и километровых выигрышей
Теперь, когда проведена вся необходимая подготовительная работа, приступим непосредственно к решению задачи.
ПОШАГОВОЕ ОПИСАНИЕ АЛГОРИТМА КЛАРКА-РАЙТА.
Демонстрация использования данного алгоритма применительно к рассматриваемой задаче приводится в табл. 4 и соответствующих комментариях к ней.
Шаг 1.
На матрице километровых выигрышей находим ячейку (i*, j*) с максимальным километровым выигрышем Smax:
При этом должны соблюдаться следующие три условия:
- пункты i* и j* не входят в состав одного и того же маршрута;
- пункты i* и j* являются начальным и/или конечным пунктом тех маршрутов, в состав которых они входят;
- ячейка (i*, j*) не заблокирована (т.е. рассматривалась на предыдущих шагах алгоритма).
Если удалось найти такую ячейку, которая удовлетворяет трем указанным условиям, то переход к шагу 2. Если не удалось, то переход к шагу 6.
Шаг 2.
Маршрут, в состав которого входит пункт i*, обозначим как маршрут 1. Соответственно, маршрут, в состав которого входит пункт j*, обозначим как маршрут 2.
Введем следующие условные обозначения:
N = {1, 2, …, n} – множество получателей;
– подмножество пунктов, входящих в состав маршрута 1;
– подмножество пунктов, входящих в состав маршрута 2.
Очевидно, что (согласно шагу 1, условие 1).
Рассчитаем суммарный объем поставок по маршрутам 1 и 2:
где qk – объем спроса k-го пункта, шт (см табл. 4).
Шаг 3.
Проверим на выполнение следующее условие:
где c – грузовместимость автомобиля, шт.
Если условие выполняется, то переход к шагу 4, если нет – к шагу 5.
Шаг 4.
Производим объединение маршрутов 1 и 2 в один общий кольцевой маршрут X. Будем считать, что пункт i* является конечным пунктом маршрута 1, а пункт j* – начальным пунктом маршрута 2. При объединении маршрутов 1 и 2 соблюдаем следующие условия:
- последовательность расположения пунктов на маршруте 1 от начала и до пункта i* не меняется;
- пункт i* связывается с пунктом j*;
- последовательность расположения пунктов на маршруте 2 от пункта j* и до конца не меняется.
Шаг 5.
Повторяем шаги 1-4 до тех пор, пока при очередном повторении не удастся найти Smax, который удовлетворяет трем условиям из шага 1.
Шаг 6.
Рассчитываем суммарный пробег автотранспорта.
ОПИСАНИЕ ПОСЛЕДОВАТЕЛЬНОГО РЕШЕНИЯ МЕТОДОМ КЛАРКА_РАЙТА.
Весь ход последовательного решения задачи представлен в таблице 4.
Таблица 4. Ходы и промежуточные результаты решения задачи
Графа 1 – номер итерации.
Графы 2, 3 – номера пунктов i* и j*, которые обозначают ячейку с максимальным километровым выигрышем Smax = s(i*,j*), найденную в результате просмотра матрицы километровых выигрышей (см. табл. 3).
Графа 4 – значение максимального километрового выигрыша Smax.
Графы 5, 6 и 7 – результаты проверки условий 1, 2 и 3 при выполнении шага 1. “+” – положительный результат, “–” – отрицательный результат.
Графы 8 и 9 – объем перевозок по маршруту 1, в состав которого входит пункт i* (q1), и маршруту 2, в состав которого входит пункт j* (q2).
Графа 10 – проверка на условие , где c – грузовместимость транспортного средства. “+” – положительный результат проверки условия, “–” – отрицательный результат.
Графа 11 – порядковый номер кольцевого маршрута (всего в ходе решения получено всего четыре кольцевых маршрута, см. рис. 4).
Графа 12 – структура кольцевого маршрута, образовавшегося на данной итерации.
Рисунок 4. Графическое представление оптимальной схемы доставки
Рассмотрим, как происходит поэтапный поиск оптимального решения задачи. Начнем с того, что исходный план развозки состоит из 12 радиальных маршрутов, когда доставка груза в каждый из пунктов назначения осуществляется по отдельному маршруту (см. рис. 2). При этом общий пробег автотранспорта составляет (см. треугольную матрицу расстояний, табл. 3):
L0 = 2*d01 + 2*d02 + ... + 2*d012 = 2*7.0 + 2*4.0 + 2*12.4 + 2*5.1 + ... + 2*7.3 = 195 км.
Теперь начнем пошаговый переход к новому оптимальному решению задачи, которое за счет объединения радиальных маршрутов в кольцевые позволит уменьшить суммарный пробег автотранспорта (графически это новое решение представлено на рис. 4).
Итерация 1.
- Объединяем два радиальных маршрута: 0-8-0 (объем доставки 200 шт.) и 0-3-0 (объем доставки 400 шт.) в общий кольцевой маршрут (под № 1) 0-8-3-0 (объем доставки 600 шт.). При этом суммарный пробег автотранспорта сокращается на 23,0 км.
Итерация 2.
- К кольцевому маршруту № 1– 0-8-3-0 (600 шт.) присоединяем радиальный маршрут 0-5-0 (150 шт.). При этом пункт 5 присоединяем к пункту 8, в результате чего получаем новую структуру кольцевого маршрута 0-5-8-3-0 (750 шт.). Суммарный пробег автотранспорта сокращается еще на 21,4 км.
- Отметим важность соблюдения последовательности пунктов в кольцевом маршруте: именно 0-5-8-3-0, а не 0-5-3-8-0 или 0-8-3-5-0.
- Если i* = 8 и j* = 5, то после объединения они должны стоять на маршруте друг за другом.
Итерация 3.
- Объединение пунктов 3 и 5 обеспечило бы выигрыш в 17,2 км. Но это объединение невозможно, поскольку оба пункта уже входят в состав кольцевого маршрута №1 – 0-5-8-3-0, а объединять можно пункты только из разных маршрутов. Таким образом, констатируем нарушение условия 1 и переходим к следующей итерации.
Итерация 4.
- К кольцевому маршруту № 1 – 0-5-8-3-0 (750 шт.) присоединяем радиальный маршрут 0-12-0 (150 шт.). При этом пункт 12 присоединяем к пункту 3, в результате чего получаем новую структуру кольцевого маршрута 0-5-8-3-12-0 (1300 шт.). Суммарный пробег автотранспорта сокращается на 14,6 км.
Итерация 5.
- Пункты 12 и 8 не объединяем, поскольку они уже входят в состав кольцевого маршрута 1 (нарушается условие 1).
Итерация 6.
- Объединяем два радиальных маршрута: 0-1-0 (450 шт.) и 0-11-0 (475 шт.) в общий кольцевой маршрут (под № 2) 0-11-1-0 (925 шт.). При этом суммарный пробег автотранспорта сокращается на 13,4 км.
Итерация 7.
- Пункты 3 и 6 нельзя объединить по причине нарушения условия 2. Пункт 3 входит в состав кольцевого маршрута 1, и в этом маршруте он занимает «промежуточное» положение, то есть он связан с пунктами 8 и 12: 0-5-8-3-12-0. Радиальный маршрут 0-6-0 можно было бы присоединить к кольцевому маршруту 1 со стороны его «крайних» пунктов – 5 или 12, но к «промежуточным» пунктам 3 и 8 его присоединить нельзя.
Итерации с 8 по 20
- Повторяют ту же логику рассуждений, что и в предыдущих 7 итерациях. Отметим только, что на итерациях 9, 11, 12, 16 и 18 объединение не производится только по причине нарушения условия
Итерации с 21 по 60
- Уже не имеют смысла, поскольку их выполнение уже не повлечет за собой изменение плана развозки.
Суммарный километровый выигрыш за 20 итераций составляет:
S = 23,0 + 21,4 + 14,6 + 13,4 + 8,8 + 8,3 + 7,9 + 7,8 = 105,3 км
а общий пробег автотранспорта, соответственно:
L1 = L0 – S = 195 –105,3 = 89,7 км
Графически оптимальная схема развозки представлена на рис. 4. Как видно, оптимальная схема развозки включает в себя четыре кольцевых маршрута (вместо первоначальных 12 радиальных маршрутов). Суммарный пробег автотранспорта можно также определить по следующей формуле:
, где Li – протяженность i-го маршрута, км; r – количество маршрутов.
Рассмотрим, например, кольцевой маршрут 0-5-8-3-12-0. Протяженность маршрута определяется по формуле (см. табл. 4):
L1 = d0,12 + d12,3 + d3,8 + d8,5 + d5,0 = 7,3 + 5,1 + 4,1 + 5,4 + 12,0 = 33,9 км.
Аналогично рассчитываем протяженность остальных маршрутов.
РЕЗУЛЬТАТЫ РЕШЕНИЯ.
Результаты решения задачисведены в таблицу:
Вступайте в нашу телеграмм-группу Инфостарт
