Общая задача поиска интервалов, включающих заданное значение.
Рассмотрим следующую, достаточно общую задачу:
Пусть имеется таблица с колонками: "ключ", "начало интервала", "конец интервала", "значение".
Таблица "Дано":
| Ключ | Начало интервала | Конец интервала | Значение |
|---|---|---|---|
| 1 | D11 | D12 | X1 |
| 2 | D21 | D22 | X2 |
| ... | ... | ... | ... |
| N | DN1 | DN2 | XN |
Требуется выбрать записи, актуальные на заданный момент времени.
Запрос, решающий данную задачу, имеет вид
ВЫБРАТЬ * ИЗ Дано
ГДЕ &МоментВремени МЕЖДУ НачалоИнтервала И КонецИнтервала
Проблема данного запроса в том, что индексация таблицы "дано" по полям "начало интервала" или "конец интервала" в общем случае недостаточно эффективна. В худшем случае, когда момент времени расположен в середине истории, область поиска сужается индексом только наполовину. В результате всю половину записей, подходящих под одно из условий вхождения в интервал, приходится просматривать сканированием, чтобы проверить выполнение второго условия. Естественно, при увеличении числа записей происходит пропорциональный рост времени выполнения запроса.
Теоретически для решения подобных задач в разных СУБД обычно применяются spatial индексы или R-деревья. Spatial индексы предполагают введение некоторой сетки, а R-деревья - использование специальной структуры данных. Хотя и то и другое возможно смоделировать имеющимися в 1С средствами, предлагается несколько другой путь.
Он основан на следующем жизненном наблюдении: при удалении от отрезка на большое расстояние он начинает выглядеть как точка, при этом близкие точки на большом удалении сливаются. То есть для возможности определения попадания точки на отрезок их нужно рассмотреть с расстояния, когда отрезок превратится в точку. Если результат превращения отрезка будет "сливаться" с заданной точкой, то существует вероятность их пересечения.
Практически "рассмотреть отрезок издалека, чтобы он превратился в точку" означает изменить масштаб представления данных отрезка: разделить все данные нацело на число, не меньшее размера отрезка. Поскольку интервалы имеют, как правило, разные размеры, предлагается использовать двоичный ряд: в зависимости от размера отрезка делить его нацело на наименьшее подходящее число (наименьшее не меньшее) из ряда степеней двойки: 1, 2, 4, 8, 16 и так далее.
В итоге получается, что нужно последовательно делить обе границы интервала на одно и то же число из ряда 1, 2, 4, 8, 16 и так далее, пока округленные значения результатов деления в конце концов не совпадут. Этот одинаковый для двух границ результат деления и будет значением специального реквизита "проекция", который можно проиндексировать и затем использовать для поиска.
Для поиска интервала по заданному значению момента времени потребуется представить его во всех возможных масштабах и выполнить проверку совпадения этих представлений со значением реквизита "проекция". Число всех возможных масштабов для диапазона 1.01.0001 - 31.12.3999 равно 36-ти. Совпадение не означает однозначного вхождения точки в интервал, а говорит только о возможности такого вхождения. Потребуется дополнительная проверка. Но эта проверка выполняется для очень небольшого количества записей, что и дает ускорение.
В результате вместо исходного запроса становится возможным использовать его более быструю версию, которая будет выглядеть следующим образом:
ВЫБРАТЬ * ИЗ РегистрСведений.Дано
ГДЕ Проекция В (&МассивПроекций) И &МоментВремени МЕЖДУ НачалоИнтервала И КонецИнтервала
Предполагается, что поле "проекция" будет проиндексировано.
Для реализации данного метода потребуется две небольших функции.
Функция ПроекцияИнтервала(От, До) Экспорт
Если Мин(От, До) = '00010101' ИЛИ Макс(От, До) = '39991231235959' Тогда
Возврат 0
КонецЕсли;
Масштаб = pow(2, 99 - Цел(99 - Окр(log(Макс(До - От, От - До)) / log(2), 10)));
Пока Окр((От - '00010101') / Масштаб) <> Окр((До - '00010101') / Масштаб) Цикл
Масштаб = Масштаб * 2
КонецЦикла;
Возврат Окр((От - '00010101') / Масштаб)
КонецФункции
Функция МассивПроекций(Дата) Экспорт
Ответ = Новый Массив;
Проекция = Дата - '00010101';
Пока Проекция >= 0.25 Цикл
Ответ.Вставить(0, Окр(Проекция));
Проекция = Проекция / 2
КонецЦикла;
Возврат Ответ
КонецФункции
Первая функция вычисляет значение спецреквизита "проекция" по началу и концу интервала, а вторая создает массив проекций по выбранному моменту времени, который затем будет использоваться для поиска.
К тексту функций необходимы небольшие пояснения:
Кажущееся сложным выражение:
Масштаб = pow(2, 99 - Цел(99 - Окр(log(Макс(До - От, От - До)) / log(2), 10)));
всего лишь вычисляет нужный элемент ряда степеней двойки, не меньший размера интервала. То есть для числа 42, например, это выражение будет равно 64, а для 73 будет равно128. Вычисление приближения масштаба в одном выражении позволяет избавиться от многих итераций цикла при его последовательном подборе.
Сравнение
Окр((От - '00010101') / Масштаб) <> Окр((До - '00010101') / Масштаб)
только на первый взгляд можно заменить выражением
Цел((От - '00010101') / Масштаб) <> Цел((До - '00010101') / Масштаб)
Дело в том, что в последнем случае интервал в две переходящих "новогодних" секунды 20151231235959 - 201601010000 (упрощенно), приходящиеся на момент переноса разряда при двоичной нумерации интервалов, будет требовать большого масштаба уменьшения и получать при таком подходе незаслуженно маленькое значение проекции. То есть произойдет "эскалация" уровня некоторых "несчастливых" интервалов. В результате они будут болтаться на верхних, не своих уровнях, отбираясь по проекции с большой, а по дополнительной проверке - с очень малой вероятностью.
Чтобы этого не происходило, потребуется при построении системы координат каждый раз сдвигать начало следующего, более нижнего уровня разметки границ интервалов на половину масштабного деления.
Это гарантирует равномерность плотности границ интервалов разного масштаба при проекции на общую ось времени. И снижение вероятности того, что интервал, переходящий через границу на нижнем уровне, тоже попадет на границу уровнем выше. Использование округления вместо расчета целого как раз и решает таким образом указанную проблему.
Та же самая мысль иллюстрируется сравнением кодовых линеек обычного двоичного позиционного кода и кода Грэя, представленных на фиг.1 и 2 соответственно.


Из рисунков видно, что в обычном позиционном двоичном коде границы интервалов разных уровней могут совпадать по вертикали, а в линейке кода Грэя этого нет. Впрочем, код Грэя упоминается здесь только номинально, в силу чудесного совпадения принципов построения его кодовой линейки и построения, иллюстрирующего использование округления.
Используя линейку кода на фиг.2, можно еще раз объяснить принцип работы метода:
Интервал каждой записи прикладывается к кодовой линейке последовательно на нулевой (нижний), первый, второй и так далее уровни пока он не войдет целиком в область, окрашенную в один цвет. Адрес этой области определяется порядковым номером области на соответствующем уровне. Этот "адрес" записывается в колонку "проекция". Для поиска интервалов, содержащих заданный период, просматриваются только интервалы, входящие в области разных уровней, в которые также входит период.
Построение фиг.2 также наглядно иллюстрирует факт отсутствия пересечений диапазонов изменений значений проекций разных уровней. Очевидно, что это может произойти только в том случае, когда нижняя граница рабочего диапазона дат меньше верхней более чем вдвое. Например, при использовании рабочего диапазона 01.01.1007 - 01.01.2016. Такой диапазон в реальных применениях не встречается. Впрочем, даже наличие пересечения не было бы фатальным, а приводило всего лишь к небольшому снижению избирательности отбора по полю "проекция".
Если есть сомнения в селективности индекса по полю "проекция", то для проверки можно сгенерировать таблицу случайных интервалов с колонками: начало интервала, конец интервала и рассчитать энтропию поля "проекция". Для этого возьмем, например, 1 000 000 интервалов, равномерно распределенных на промежутке времени длинной один год, средней длиной один день с экспоненциальным распределением длины. Просматривая полученные значение поля, можно увидеть большое разнообразие записанных в нем значений. Вычисления показывают, что энтропия поля префикс равна примерно 8,5.
Это можно было бы предсказать и теоретическими вычислениями.
Достаточная энтропия показывает, что расчет на то, что план выполнения запроса будет использовать индекс, включающий поле "проекция", имеет надежное основание. Энтропия может снизиться до недостаточных значений только когда средняя длина интервала станет сравнима с длиной истории, но в этом случае не поможет (будет не нужен) ни один метод.
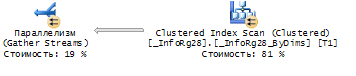
Вот план выполнения улучшенной версии запроса:


А вот данные тестирования времени его выполнения в зависимости от количества записей:
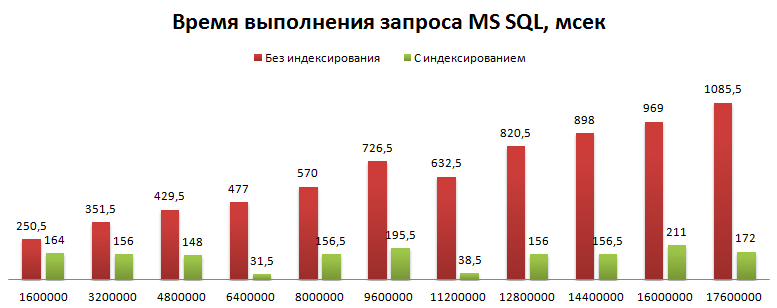

Видно, что время выполнения запроса от количества записей практически не зависит, хотя в теории логарифмическая зависимость определенно имеется. Она связана с выполнением поиска на Log(n) уровнях.
Для сравнения на том же графике приведено время выполнения обычного запроса, которое имеет видимую на графике зависимость от количества записей.
Тестирование проводилось при следующих параметрах: Для файлового варианта: 500 тысяч интервалов в год (случайно-равномерно по году), длина каждого интервала случайная (экспоненциальный закон), со средним 86400 секунд (сутки). Замеры за один, два, три и четыре года. Выбранный момент времени помещался в середине диапазона. Для MS SQL 1,6 миллиона заявок в год, диапазон от одного года до 11 лет, средний размер и положение интервала такие же как в варианте для файловой базы.
Для удобства проверки полученных результатов к статье прилагается каркасная конфигурация, содержащая обработки заполнения базы тестовыми данными и отчеты для сравнительного тестирования базового метода "0" и предлагаемого метода "1".
В заключение можно сказать, что метод легко уточняется на случаи, когда интервалы выражаются днями или представляют собой отрезки числовой прямой с дискретными координатами. А также обобщается на случай нахождения пересечений интервалов.
Интересной теоретической задачей является расчет "коэффициента полезного действия" предлагаемого индекса в зависимости от основания системы счисления, то есть процента лишних интервалов, фильтруемых дополнительной проверкой. Возможно, в каких-то случаях было бы выгодно выбирать другое основание - это еще одно направление дальнейших исследований. Также достаточно интересны запросы, определяющие пересечение интервалов, использующие поле "проекция". Эти запросы в статье не приведены, чтобы не отвлекать внимание от сути метода.
Подводя итог, можно еще раз повторить, что простота предложенного решения заключается в добавлении к записям, содержащим интервалы, всего одного дополнительного реквизита. Этот реквизит позволяет использовать при поиске интервалов, содержащих заданное значение, дополнительные высокоселективные условия равенства совместно с условиями неравенства. В результате при минимальных изменениях структуры запросов время их выполнения существенно уменьшается и к тому же перестает зависеть от объема накопленных данных.
В качестве примера использования предложенного запроса можно рассмотреть одну более конкретную и достаточно популярную задачу.
Задача о статусах заявок
В обсуждении статьи "Регистры сведений 1С. Как это устроено" в комментарии (40) была очень подробно сформулирована простая задача, подчеркивающая врожденный недостаток периодических регистров сведений. Он заключается в том, что при хранении в периодическом регистре сведений статусов заявок, затраты времени на выборку заявок с конкретным статусом неизбежно растут вместе с ростом глубины истории статусов заявок.
То есть речь идет о деградации производительности вот такого запроса:
ВЫБРАТЬ * ИЗ РегистрСведений.СтатусыЗаявок.СрезПоследних(&Т0, )
ГДЕ Статус В (&Новый, &ВРаботе)
к регистру сведений вот такой структуры:
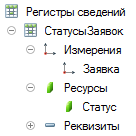
Например, если заявки поступают каждые десять секунд, то через три года их станет десять миллионов и время выполнения этого запроса возрастет (учтены конкретные условия задачи) до 16,4 секунд. Анализ показывает, что данная проблема имеет общую природу с той, которая решается методом, приведенным в данной статье.
Поэтому предлагается добавить к структуре регистра два реквизита: "проекция" типа Число (15, 0) и "дата смены статуса" типа "Дата".
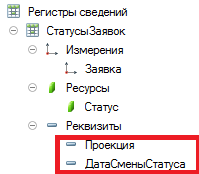
И использовать для получения списка заявок, имеющих нужные статусы на любой заданный момент, вот такой запрос:
ВЫБРАТЬ *
ИЗ РегистрСведений.СтатусыЗаявок
ГДЕ Проекция В(&МассивПроекций) И Период <= &Т0 И ДатаСменыСтатуса > &Т0
Чтобы не ломать структуру регистра и учитывая то, что стандартные индексы регистра сведений не могут одновременно включать два реквизита или реквизит и ресурс, пришлось пойти на небольшую хитрость: при расчете поля "проекция" добавлять к результату номер статуса, умноженный на миллион миллионов. То есть фактически поле "проекция" объединило в предлагаемом решении в себе значение двух полей "статус" и "проекция". Что и позволило использовать в запросе стандартное индексирование реквизита "проекция".
В результате время выборки заявок с нужным статусом уменьшилось до 0,57 секунды и практически перестало зависеть от числа заявок в базе!
Вот новый план выполнения запроса:
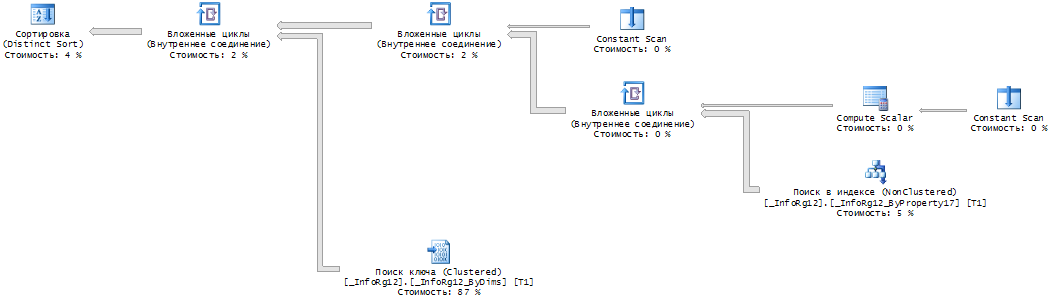
Каркасную конфигурацию "СтатусыЗаявок" с запросами "Задача1" и "Задача2" можно также скачать из приложений к статье.
P.S.: Хочу поблагодарить Александра Спешилова (speshuric) за интересную задачу, благодаря которой было найдено описанное решение, а Сергея Носкова (Sergey.Noskov) за статью о регистрах сведений, пробудившую интерес к данной теме.
.
Вступайте в нашу телеграмм-группу Инфостарт