Для чего эта публикация;
- Показать решение редкой задачи. В поисковиках можно найти решение похожих задач, но может кому и пригодится как готовое решение.
- Показать возможность работы с деревом значений без использования рекурсии. Почему-то с этим объектом всегда работают только через рекурсию
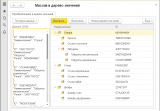
Итак, на входе мы имеем JSON, полученный от сервера Google, с помощью API DRIVE. А также желание отобразить пользователю его же папки, но в форме 1С.
| Входящие данные - строку JSON вида: | И желаемый результат, который нужно показать пользователю |
|
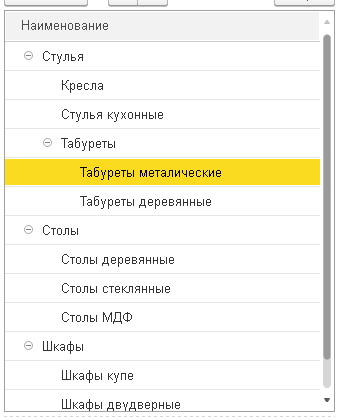 |
Из строки json такого вида мы с легкостью можем получить массив структур, с которым и будем работать. Для отображения на форме нам из массива нужно получить дерево значений. Бродя по просторам Инфостарт нашел только одно решение (извините, возможно плохо искал) : Пример преобразования дерева значений в таблицу значений и обратно в 1Cv8. Но автор использует в качестве Ключей и КлючейСвязи числовые значения. Также все это происходит в ТаблицаЗначений , где есть внутренние методы сортировки и поиска. В структурах же этого нету. Конечно, первой же идеей было воспользоваться промежуточным вспомогательным объектом ТаблицаЗначений, в котором и определить эти ключи. Но это решение мне не нравится - оно заберет вычислительные ресурсы. Также мне не нравится использование рекурсии в таких задачах - привет Стиву Макконелу и его отношению к рекурсии. Тем более рекурсия снова же достаточно много кушает ресурсов.
Если мы не хотим использовать ТаблицуЗначений, значит в нашем распоряжении есть неизменный спутник массива - цикл обхода массива. И жаль, но обходить придется несколько раз. Это тоже меня не устраивает, поэтому количество обходов нужно сократить до минимума.
Для последующего объяснения алгоритма я воспользуюсь несколько упрощенными начальными данными: пускай это будет массив структур, в каждой из которых будет по два свойства "Родитель" и "Наименование" (Ключ и КлючСвязи соответсвенно). Причем эти свойства будут содержать в себе непосредственно наименования наших отображаемых данных:
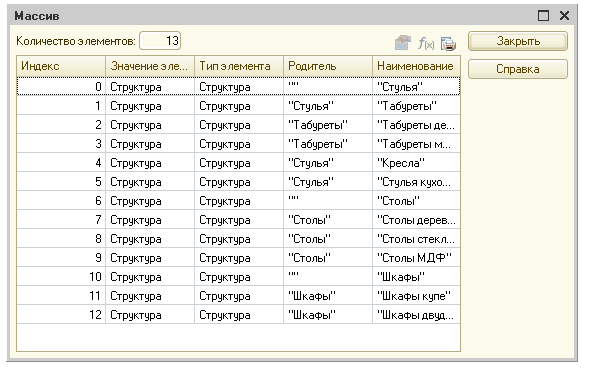
И так, первое что мы делаем это создаем ДеревоЗначений, добавляем нужные колонки и создаем корневые строки. Для этого нужно пройти по всему массиву и посмотреть заполнено ли у каждой структуры свойство "Родитель". И если не заполнено, тогда добавить в дерево как корневой элемент;
МассивДанных = ПолучитьМассивСтруктур();
ДеревоРезультат = Новый ДеревоЗначений;
ДеревоРезультат.Колонки.Добавить("Наименование");
КоличествоЭлементов = МассивДанных.Количество(); //Для кэша, и понадобиться нам
Для Сч = 0 По КоличествоЭлементов - 1 Цикл
ЭлементДанных = МассивДанных[сч];
Если Не ЗначениеЗаполнено(ЭлементДанных.Родитель) Тогда
СтрокаДЗ = ДеревоРезультат.Строки.Добавить();
СтрокаДЗ.Наименование = ЭлементДанных.Наименование;
КонецЕсли;
КонецЦикла;
Так... Начало заложено :). Теперь мы должны взять у каждого корневого элемента значение свойства "Наименование" и найти структуры с этим значением в свойстве "Родитель". Но ведь это несет в себе определенные затраты.
Нам придется в поиске проходить все элементы заново. В том числе и корневые элементы массива, среди которых нам уже искать не нужно.
Для решения этой проблемы я воспользуюсь все-таки сортировкой. Все обработанные элементы я буду ставить в начало массива, и при этом запоминать индекс, который еще не обработан - индекс струтуры в массиве, которая еще не добавлена в ДеревоЗначений
МассивДанных = ПолучитьМассивСтруктур();
ДеревоРезультат = Новый ДеревоЗначений;
ДеревоРезультат.Колонки.Добавить("Наименование");
КоличествоЭлементов = МассивДанных.Количество();
ИндексОбработки = 0; // Индекс элемента массива, еще не помещенного в дерева значений
Для Сч = 0 По КоличествоЭлементов - 1 Цикл
ЭлементДанных = МассивДанных[сч];
Если Не Заполнено(ЭлементДанных.Родитель) Тогда
СтрокаДЗ = ДеревоРезультат.Строки.Добавить();
СтрокаДЗ.Наименование = ЭлементДанных.Наименование;
Если сч = ИндексОбработки Тогда
ИндексОбработки = ИндексОбработки+1; // Перемещать не нужно
Продолжить;
КонецЕсли;
//Перемещаем обработанный элемент в начало массива и увеличиваем индекс обработки
МассивДанных[сч] = МассивДанных[ИндексОбработки];
МассивДанных[ИндексОбработки] = ЭлементДанных;
ИндексОбработки = ИндексОбработки+1;
КонецЕсли;
КонецЦикла;
Вот теперь все более в порядке. Нам не нужно производить поиск среди всех элементов, а начинать только с тех, которые не помещены в ДеревоЗначений.
Теперь возникает задача: как обойти все строки ДереваЗначений, при этом не использовать рекурсию. Для этого я решил воспользоваться вспомогательным объектом. Это будет массив, в который я буду помещать ссылки на наши добавленные строки по порядку их добавления. Это не сильно увеличит ресурсозатраты, потому что в массиве будут содержаться только ссылки на строки, а не сами данные.
В следующем коде я покажу конечный результат моих изысканий. Будет два цикла. Первый - наш цикл заполнения корневых элементов, в котором тут же будем добавлять во вспомогательный массив наши добавленные строки. А второй - проход по вспомогательному массиву в поиске дочерних строк.
Также я добавлю несколько проверок, для того чтобы завершить второй цикл когда все элементы были проверены, а также для того чтобы корректно обработать входящие данные с испорченной структурой (например элемент с несуществующим родителем, или зацикливание подчинения).
МассивДанных = ПолучитьМассивСтруктур();
ДеревоРезультат = Новый ДеревоЗначений;
ДеревоРезультат.Колонки.Добавить("Наименование");
КоличествоЭлементов = МассивДанных.Количество();
ИндексОбработки = 0;
МассивСтрок = Новый Массив(КоличествоЭлементов); // Наш вспомогательный массив
//Заполнение корневых элементов
Для Сч = 0 По КоличествоЭлементов - 1 Цикл
ЭлементДанных = МассивДанных[сч];
Если НЕ ЗначениеЗаполнено(ЭлементДанных.Родитель)Тогда
МассивСтрок[ИндексОбработки] = ДеревоРезультат.Строки.Добавить();
ЗаполнитьЗначенияСвойств(МассивСтрок[ИндексОбработки],ЭлементДанных);
Если сч = ИндексОбработки Тогда
ИндексОбработки = ИндексОбработки+1;
Продолжить;
КонецЕсли;
МассивДанных[сч] = МассивДанных[ИндексОбработки];
МассивДанных[ИндексОбработки] = ЭлементДанных;
ИндексОбработки = ИндексОбработки+1;
КонецЕсли;
КонецЦикла;
//Поиск дочерних элементов
Для Сч = 0 По КоличествоЭлементов - 1 Цикл
Если ИндексОбработки = КоличествоЭлементов ИЛИ Сч = ИндексОбработки Тогда
//Если ИндексОбработки достигнет конца массива, нам больше незачем искать дочерние элементы
// Если Сч станет равным ИндексОбработки, это свидетельствет о зацикленности подчинения
Прервать;
КонецЕсли;
КлючПоиска = МассивДанных[сч].Наименование;
Для Сч2 = ИндексОбработки По КоличествоЭлементов - 1 цикл
ЭлементДанных = МассивДанных[Сч2];
Если ЭлементДанных.Родитель = КлючПоиска Тогда
МассивСтрок[ИндексОбработки] = МассивСтрок[Сч].Строки.Добавить();
ЗаполнитьЗначенияСвойств(МассивСтрок[ИндексОбработки],ЭлементДанных);
Если Сч2 = ИндексОбработки Тогда
ИндексОбработки = ИндексОбработки+1;
Продолжить;
КонецЕсли;
МассивДанных[Сч2] = МассивДанных[ИндексОбработки];
МассивДанных[ИндексОбработки] = ЭлементДанных;
ИндексОбработки = ИндексОбработки+1;
КонецЕсли;
КонецЦикла;
КонецЦикла;
Да, я соглашусь , что можно сделать это и в одном цикле, ведь здесь наблюдается повторное использование кода. Но я оставил два цикла для удобочитаемости.
Таким же методом, без использования рекурсии, возможна и обратная процедура. Например вывод ДереваЗначений в сообщения. Только тут для удобства нужно выводить еще и уровень, потому снова воспользуюсь массивом структур:
МассивСтрок = Новый Массив;
КолонкиДЗ = ДеревоЗначений.Колонки;
Для Каждого СтрокаДЗ из ДеревоЗначений.Строки Цикл
МассивСтрок.Добавить(СтрокаДЗ);
КонецЦикла;
Сч = 0;
Пока Сч < МассивСтрок.Количество() Цикл
СтрокаДЗ = МассивСтрок[Сч];
Отступы = "";
Для КоличествоОтступов = 1 По СтрокаДЗ.Уровень() Цикл
Отступы = Отступы + Символы.Таб;
КонецЦикла;
СтрокаОтборажения = Отступы;
Для Каждого КолонкаДерева из КолонкиДЗ Цикл
СтрокаОтборажения = СтрокаОтборажения + Строка(СтрокаДЗ[КолонкаДерева.Имя]) + "| ";
КонецЦикла;
Сообщить(СтрокаОтборажения);
Для Каждого ПодстрокаДЗ из СтрокаДЗ.Строки Цикл
МассивСтрок.Вставить(Сч+1,ПодстрокаДЗ);
КонецЦикла;
Сч = Сч +1;
КонецЦикла;
Интересное замечание, которое было получено в ходе тестирования обработки: если создать у ДереваЗначений колонку "Родитель" или "Parent", то ее никак не будет возможно заполнить, потому что у строки ДереваЗначений есть предопределенное свойство "Родитель" или англоязычный аналог "Parent" .
Прикрепляю обработку для тестирования данного алгоритма. В ней алгоритм имеет более универсальный функционал
Вступайте в нашу телеграмм-группу Инфостарт