В большинстве реляционных СУБД в качестве структуры данных для индексов (та или иная их реализация) используются именно деревья. И не просто деревья, а сбалансированные деревья поиска. В этой статье как раз о них.
Сами по себе деревья бесполезны, если мы не можем выполнять с ними определенные операции. К таким операциям обычно относят: поиск элемента, поиск минимального (максимального) элемента, вставка, удаление. В разрезе этих операций мы и рассмотрим каждое из 4 деревьев отдельно. Каждое дерево имеет свои особенности, связанные как правило с организацией хранения данных, но при этом они все связаны между собой:
- Двоичное дерево поиска и двоичная куча - это частный случай обычного двоичного дерева;
- B-дерево - это разновидность дерева поиска. Как правило не является двоичным деревом.
Теперь рассмотрим каждое дерево отдельно.
Двоичное дерево
Двоичное дерево (binary tree) - дерево, в котором каждый узел имеет не более двух потомков. Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками. В двоичном дереве могут храниться любые данные, в любом порядке.
Пример двоичного дерева:
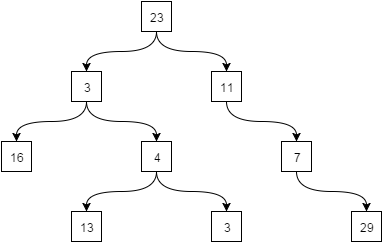
Особый интерес из себя не представляет, нужно только для понимания что такое вообще двоичное дерево. Нас интересуют следующие два дерева, которые являются его разновидностью.
Двоичное дерево поиска (binary search tree)
Двоичное дерево поиска - это двоичное дерево, для которого выполняются следующие дополнительные условия:
- Оба поддерева — левое и правое — являются двоичными деревьями поиска.
- У всех узлов левого поддерева произвольного узла X значения ключей данных меньше, нежели значение ключа данных самого узла X.
- В то время, как значения ключей данных у всех узлов правого поддерева (того же узла X) больше, нежели значение ключа данных узла X.
Пример дерева:
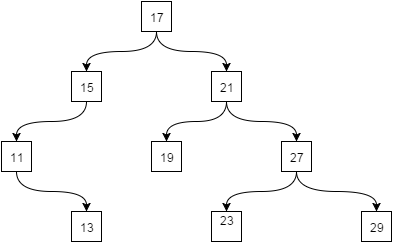
Структура дерева зависима от порядка заполнения ключей. Если мы будем заполнять предварительно отсортированными массивом ключей (например: 10; 20; 30; 40), то мы получим экстремально сбалансированное дерево. Т.е. дерево, у которого высота равна количеству элементов.
Поиск элемента
Поиск начинается с корня. При этом значение каждого узла сравнивается с искомым значением:
- Если искомое значение равно значению узла, то поиск завершен.
- Если искомое значение меньше значения узла, то переходим к обработке левого дерева.
- Если искомое значение больше значения узла, то переходим к обработке правого дерева.
Для поиска ключа 23 мы нужно 4 итерации (начинаем с корня, ключ расположен на 4 уровне):
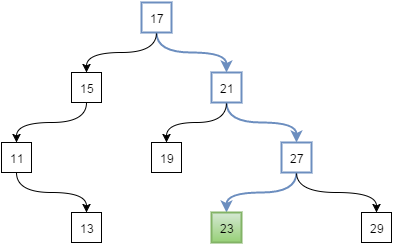
Добавление элемента
Добавление аналогично поиску элемента, только если отсутствует дочерний узел нужно создать его, вставляя добавляемый элемент. Добавим ключ 7 в дерево:
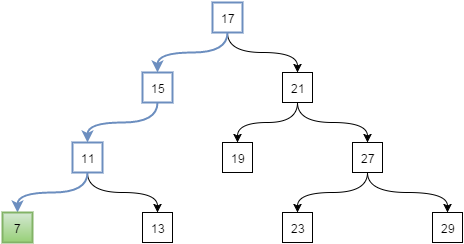
Удаление элемента
А вот операция удаления уже сложнее. Нужно сначала найти нужный нам ключ, а потом уже обработать его. Всего возможны 3 варианта:
- узел не имеет дочерних узлов;
- узел имеет один дочерний узел;
- узел имеет два дочерних узла.
Если узел не имеет дочерних узлов, то просто удаляем его. Удалим ключ 23:
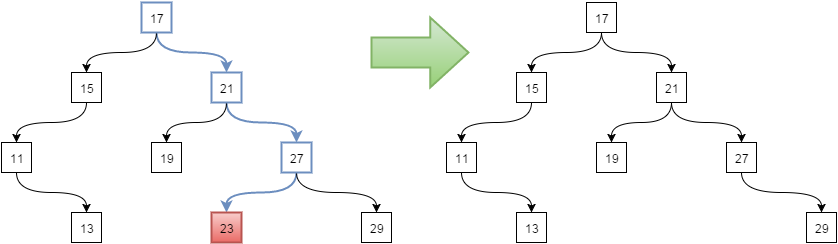
Если узел имеет только один дочерний узел, то заменяем связь с родителем узла на дочерний узел. Удалим узел 11:
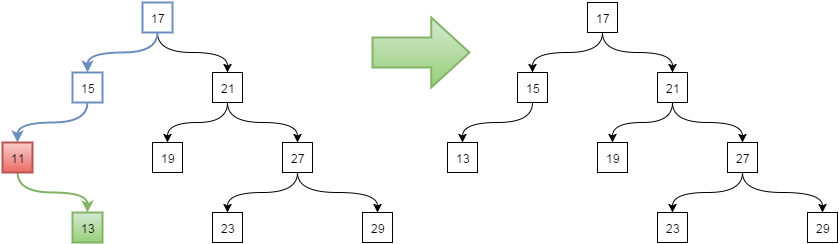
Если же узел имеет два дочерних узла, тогда надо найти следующий элемент в правом дочернем узле (т.е. минимальный узел, который не имеет дочерних узлов). Удалим узел 21:
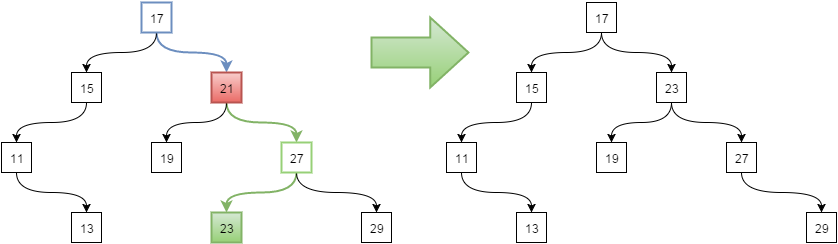
Двоичная куча (binary heap)
Двоичная куча - двоичное дерево, для которого выполнены три условия:
- Значение в любой вершине не меньше, чем значения её потомков.
- Глубина листьев (расстояние до корня) отличается не более чем на 1 уровень.
- Последний уровень заполняется слева направо.
Существуют также кучи, где значение в любой вершине, наоборот, не больше, чем значения её потомков. Структура данных как двоичная куча используется в основном в алгоритмах сортировки.
Пример двоичной кучи:
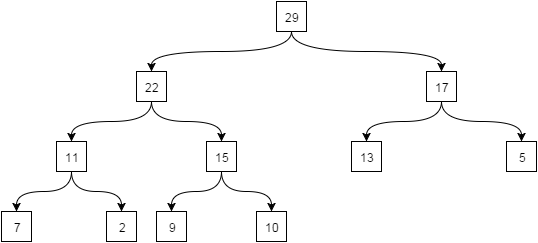
Над кучей можно выполнять следующие операции:
- Добавить элемент в кучу;
- Исключить максимальный элемент из кучи;
- Изменить значение любого элемента.
Добавление элемента
Добавление элемента всегда происходит последовательно в первый незаполненный узел, начиная сверху вниз и перемещаясь слева направо по уровню. Добавим в кучу ключ 16:
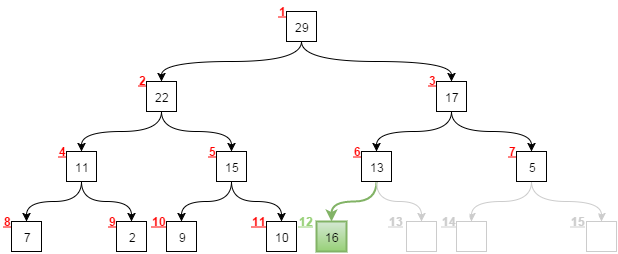
Для удобства на картинке все узлы пронумерованы, начиная с единицы (корневой узел). В нашем случае самым крайним и свободным узлом оказался узел под номером 12. Туда-то мы и записали свое значение.
Если бы на 4-ом уровне дерева все узлы были заполнены (т.е. узлы с номерами от 8 до 15), тогда мы бы добавили левый дочерний узел к элементу 8, как самому левому узлу 4-го уровня, при этом бы образовался новый 5-ый уровень.
При этом необходимо выполнить условие, что элемент родительского узла должен быть всегда больше элемента дочернего. Поэтому, если наше значение меньше значения родителя, то необходимо родителя и потомка поменять местами:
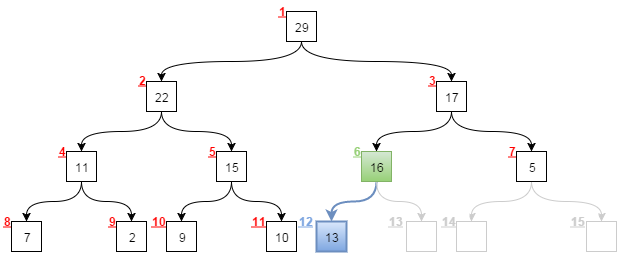
Двигаемся вверх по дереву, пока значение нашего узла не станет меньше значения родителя.
Исключение максимального элемента
Т.к. самым максимальным узлом кучи является корневой элемент, то необходимо удалить именно его. На его место записывается самый последний элемент дерева (нумерация элементов сверху вниз, слева направо):
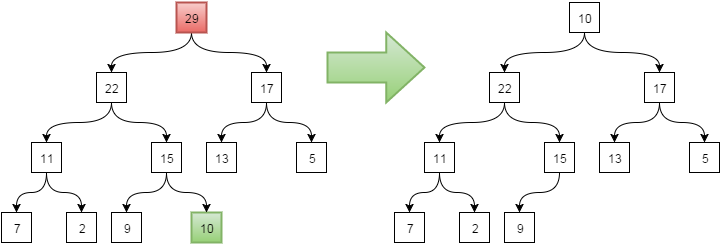
Если при этом нарушилось свойство кучи и значение узла стало меньше значения одного из дочерних узлов (или обоих), то меняем местами значение текущего узла и дочернего. Сравнение нужно делать сперва с левым дочерним узлом, затем с правым. Рекурсивно продолжать сравнение, спускаясь вниз по измененным узлам.
В нашем примере ключ 10 меньше 22 и 17, но т.к. узел с ключом 22 находится левее, то берем именно его. Далее опять сравниваем с дочерними узлами - 10 меньше 11, поэтому меняем с этим узлом. На 4-ом уровне ключ 10 уже больше 7 и 2, поэтому прекращаем операцию.
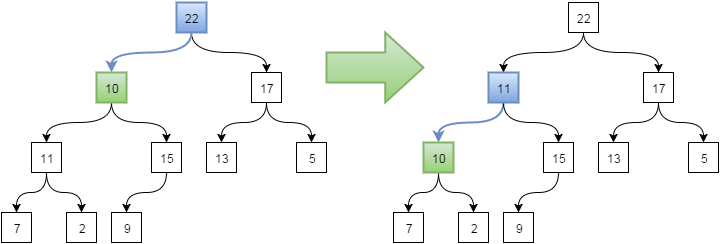
Изменение значения элемента
При изменении элемента кучи возможны два варианта:
- новое значение меньше значения исходного элемента. В этом случае необходимо менять местами дочерний и текущий узел, спускаясь вниз по дереву до тех пор, пока выполняется условие, что значение родительского узла больше значения дочернего узла (т.е. алгоритм тот же, что при исключении максимального элемента из дерева).
- новое значение больше значения исходного элемента. В этом случае нужно менять местами текущий и родительский узел, поднимаясь вверх по дереву, до тех пор, пока значение родительского узла не будет больше значения текущего узла (алгоритм аналогичен добавлению нового элемента).
B-дерево (B-tree)
B-дерево - дерево, которое является разновидностью двоичного дерева поиска. Особенностями В-деревьев является:
- сбалансированность - длина пути от корня до любого листового элемента одинакова;
- ветвистость - в отличие от двоичных деревьев каждый узел может ссылаться на множество потомков;
- отсортированность - ключи в дереве хранятся в неубывающем порядке;
- логарифмическое время работы всех стандартных операций (поиск, вставка, удаление).
B-деревья (или их разновидности) используются в индексах большинства реляционных СУБД. Оптимизированы специально для работы с дисковой подсистемой.
При построении дерева применяется параметр t, который называется минимальной степенью. Количество ключей в узле (за исключением корневого) должно быть от t – 1 до 2t – 1.
Пример B-дерева (t=3):
Стоит обратить внимание, что дочерние узлы ссылаются не на сам родитель, а разделитель между ключами этого родителя.
Поиск элемента
Алгоритм поиска элемента схож с алгоритмом двоичного дерева поиска. Обход начинается с корня. Так как все ключи хранятся в неубывающем порядке, то поиск ведем слева на право. Если ключ содержится в текущем узле, возвращаем его. Иначе определяем интервал и переходим к соответствующему потомку. Повторяем пока ключ не найден или не дошли до листа.
Добавление элемента
Добавление элемента уже интереснее. Возможны два случая:
- Если узел содержит от t-1 до 2t-2 элемента. Т.е. узел не заполнен. В этом случае просто в узел добавляется новый элемент и все.
- Если узел содержит 2t-1 ключей (узел заполнен), то при добавлении в него он разбивается на два по t-1 элемента. При этом средний элемент (медиана) узла идет в родительский узел. Соответственно, если и родительский узел был заполнен, то разбиваем и его разбиваем на два. Если разбивается корневой узел, то увеличивается высота дерева. Добавим в дерево ключ 12:
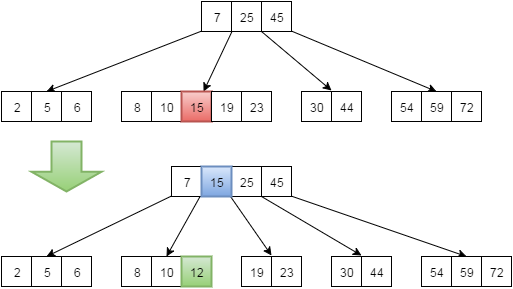
Удаление элемента
Удаление происходит сложнее, потому что при удалении происходит перестроение дерева. Удалять можно как из листового узла, так и из внутреннего.
Рассмотрим удаление из листового узла:
- Если в узле больше, чем t-1 ключей, то просто удаляем ключ.
- Если в t-1 ключей (минимальное количество) и существует соседний узел(находящийся рядом с ним и имеющий такого же родителя), который содержит больше t-1 ключей. В этом случае ближайший ключ узла-соседа перейдет в родительский узел в качестве разделителя, а ключ узла-родителя перейдет в наш узел, где мы удаляем ключ. Для примера удалим ключ 44.
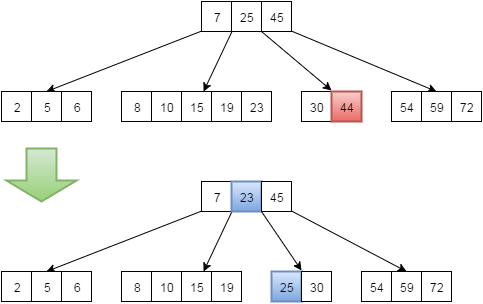
- Если в узле t-1 ключ (минимальное количество) и все соседние узлы, содержат t-1 ключ (минимальное количество), то мы объединяем его с каким-либо соседом, удаляем нужный ключ. И тот ключ из узла-родителя, который был разделителем для этих двух «бывших» соседей, переместим в наш новообразовавшийся узел (он будет в нем медианой).
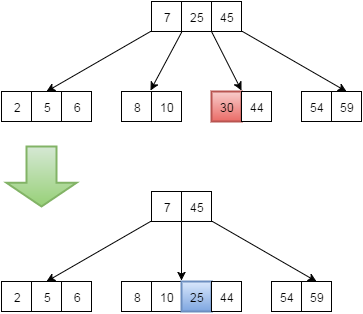
Вступайте в нашу телеграмм-группу Инфостарт
