В предыдущей статье Матричная форма записи СЛАУ для Графа затрат мы выяснили, что задачу расчета фактической себестоимости продукции (работ, услуг) можно свести к решению СЛАУ, записанной в матричном виде. Более того, специалисту по расчету себестоимости достаточно просто сформировать расширенную матрицу исходных коэффициентов, т.к. далее процедура решения СЛАУ представляет собой набор очевидных действий по расчету значений тарифов. Эти действия понятны, однозначны и легко автоматизируются. Казалось бы, что здесь еще можно обсуждать? Ведь мы уже получили удобный инструмент для решения одной из самых сложных задач бухгалтерского учета – задачи калькулирования себестоимости продукции (работ, услуг).
Но дело в том, что возможности использования Графов затрат значительно шире, чем «просто» расчет фактической себестоимости продукции (работ, услуг). И более того, из тех задач, которые можно решать с помощью Графов затрат, задача расчета фактической себестоимости является далеко не самой сложной и интересной. Поэтому, начиная с данной статьи мы рассмотрим несколько видов (классов) бухгалтерских задач, часть из которых возможно уже знакома читателям, но также будут рассмотрены и такие задачи, которые ранее даже не ставились в контексте бухгалтерского учета. В данном случае понятие «бухгалтерский учет» трактуется расширенно, предполагается, что оно относится ко всей предметной области, связанной с моделированием хозяйственных процессов предприятия.
Однако перед тем, как перейти непосредственно к рассмотрению задач на Графах затрат, необходимо кратко обсудить два важных вопроса, связанных с использованием в бухгалтерском учете методов решения СЛАУ и алгоритмов рисования Графов затрат. Что здесь важно понять? Вполне возможно, что эти разделы математики для многих учетных специалистов являются новыми, если и не в плане знаний, то в контексте их использования для решения бухгалтерских задач. На сегодняшний день эти разделы уже довольно хорошо проработаны математиками, поэтому учетным специалистам здесь можно только посоветовать не тратить драгоценное время на изобретение велосипеда – не имеет особого смысла глубоко «влезать» в изучение работы различных методов решения СЛАУ или алгоритмов укладки графов на плоскости. Да, это интересные задачи, но это задачи для математиков, а для учетного специалиста это просто готовые математические инструменты для работы с Графами затрат, которыми надо научиться пользоваться.
В автоматизированных учетных системах эти инструменты должны быть реализованы с помощью библиотек математических алгоритмов. В учебных же целях для решения СЛАУ вполне достаточно уметь пользоваться стандартным функционалом Microsoft Excel, а для рисования графов можно использовать, например, Graphviz (graphviz.org) – программное обеспечение для визуализации графов с открытым исходным кодом или, в конце концов, рисовать графы вручную. Таким образом, еще раз зафиксируем внимание читателей на том, что существует много довольно сложных именно бухгалтерских задач на Графах затрат, и было бы разумнее в первую очередь направить усилия учетных специалистов именно на их решение, а процедуры решения СЛАУ и рисования графов нужно рассматривать исключительно в качестве удобного стандартного инструментария для этого.
Теперь можно перейти к обсуждению бухгалтерских задач на Графах затрат, и в качестве первой такой задачи рассмотрим задачу расчета прогнозных значений себестоимости продукции (работ, услуг).
Задача 1. Расчет прогнозных значений себестоимости
Рассмотрим предприятие, которое осуществляет два вида деятельности – производит и продает два вида продукции. В рассматриваемом периоде Цех-4 произвел и поместил на Склад-1 первый вид продукции в количестве 10 шт, а Цех-6 произвел и поместил на Склад-2 20 кг второго вида продукции. Далее со Склада-1 вся продукция была продана за 120$, а 15 кг продукции со Склада-2 было продано за 100$. Кроме того, 5 кг продукции со Склада-2 было использовано в этом же периоде Цехом-5.
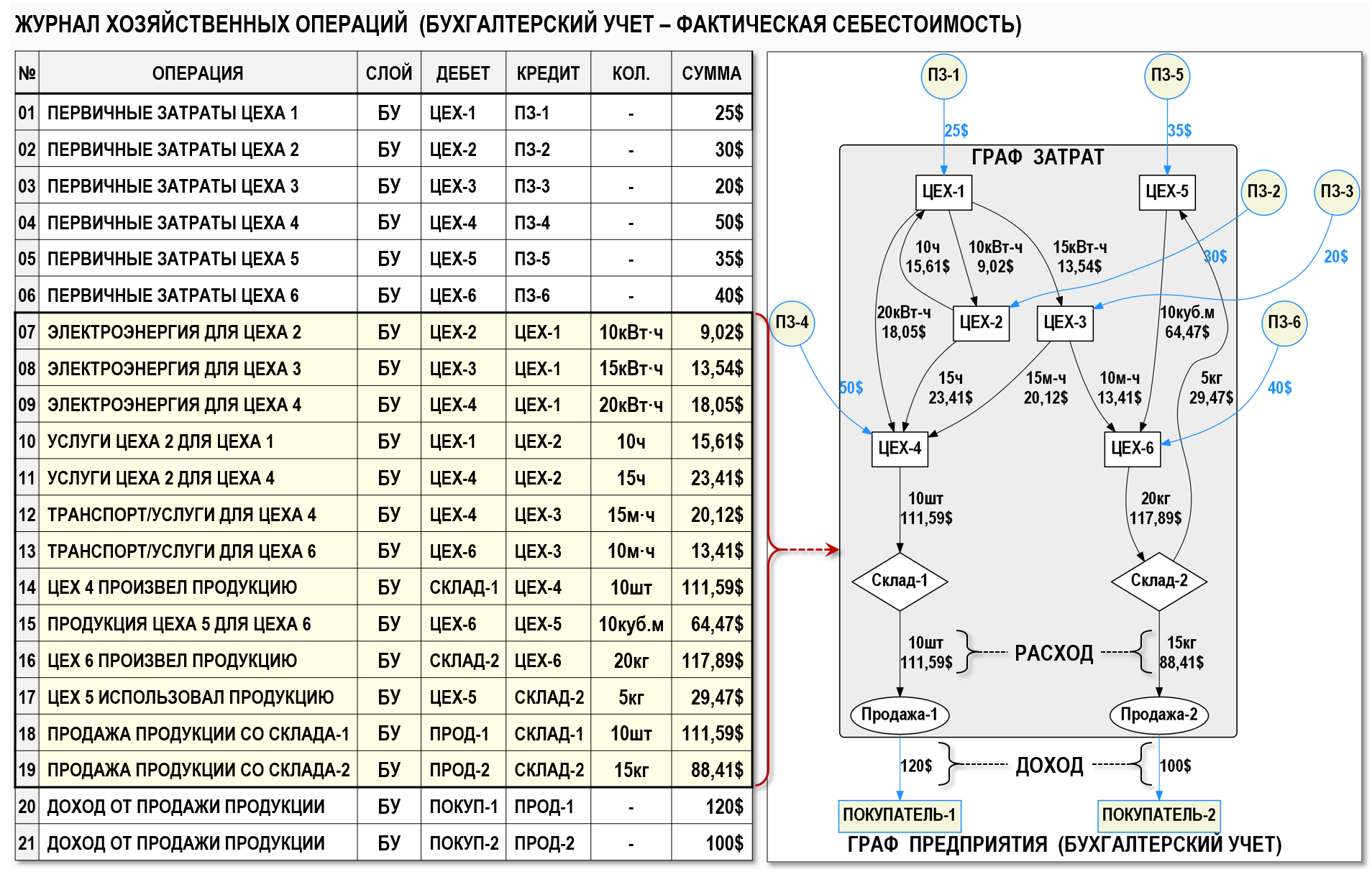
Хозяйственные операции предприятия после проведения процедуры «закрытия» затрат периода (т.е. после расчета фактической себестоимости) представлены ниже на рисунке с помощью журнала хозяйственных операций (ЖХО) и в графической форме. Мы не будем подробно описывать в текстовом виде все хозяйственные процессы предприятия, т.к. данный рисунок дает довольно ясное представление о том, как взаимодействуют между собой цеха предприятия при производстве продукции обоих видов.
В результате решения СЛАУ для Графа затрат была определена фактическая себестоимость обоих видов проданной продукции, что позволило определить финансовые результаты для каждого вида деятельности, а также общий финансовый результат:
ProfitБУ1=120$–111,59$=8,41$ (прибыль от продажи продукции со Склада-1)
ProfitБУ2=100$–88,41$=11,59$ (прибыль от продажи продукции со Склада-2)
ProfitБУ=8,41$+11,59$=20$ (общая прибыль от продажи продукции)
Предположим теперь, что стало известно о повышении цены на покупное дизельное топливо, которое Цех-1 (дизельная электростанция) использует для производства электроэнергии. В результате этого в следующем периоде необходимый объем дизельного топлива может подорожать на 5$. В связи с этим возникает необходимо понять, каким образом это повлияет на финансовые результаты для каждого вида деятельности предприятия при условии, что продажные цены на продукцию останутся неизменными. Другими словами, необходимо выяснить, каким образом увеличение на 5$ стоимости первичных затрат Цеха-1 повлияет на себестоимость обоих видов проданной продукции.
Сформулируем эту задачу с помощью расширенных матриц исходных коэффициентов, которые, как известно из предыдущей статьи, удобны тем, что позволяют представить СЛАУ в компактной и наглядной форме. Для расчета фактической себестоимости (Сценарий 1) в бухгалтерском учете формируется расширенная матрица исходных коэффициентов KEXP-БУ[11,10], а для расчета прогнозных значений себестоимости (Сценарий 2) формируется расширенная матрица исходных коэффициентов KEXP-УУ1[11,10].
Как видно выше на рисунке, матрица KEXP-УУ1[11,10] отличается от матрицы KEXP-БУ[11,10] значением только одного элемента – в первой строке правого столбца теперь стоит значение (-30), т.к. стоимость первичных затрат Цеха-1 выросла на 20% с 25$ до 30$. Значения остальных элементов матрицы остались неизменными, т.к. рассматривается тот же сценарий производственной программы предприятия, что и в предыдущем периоде.
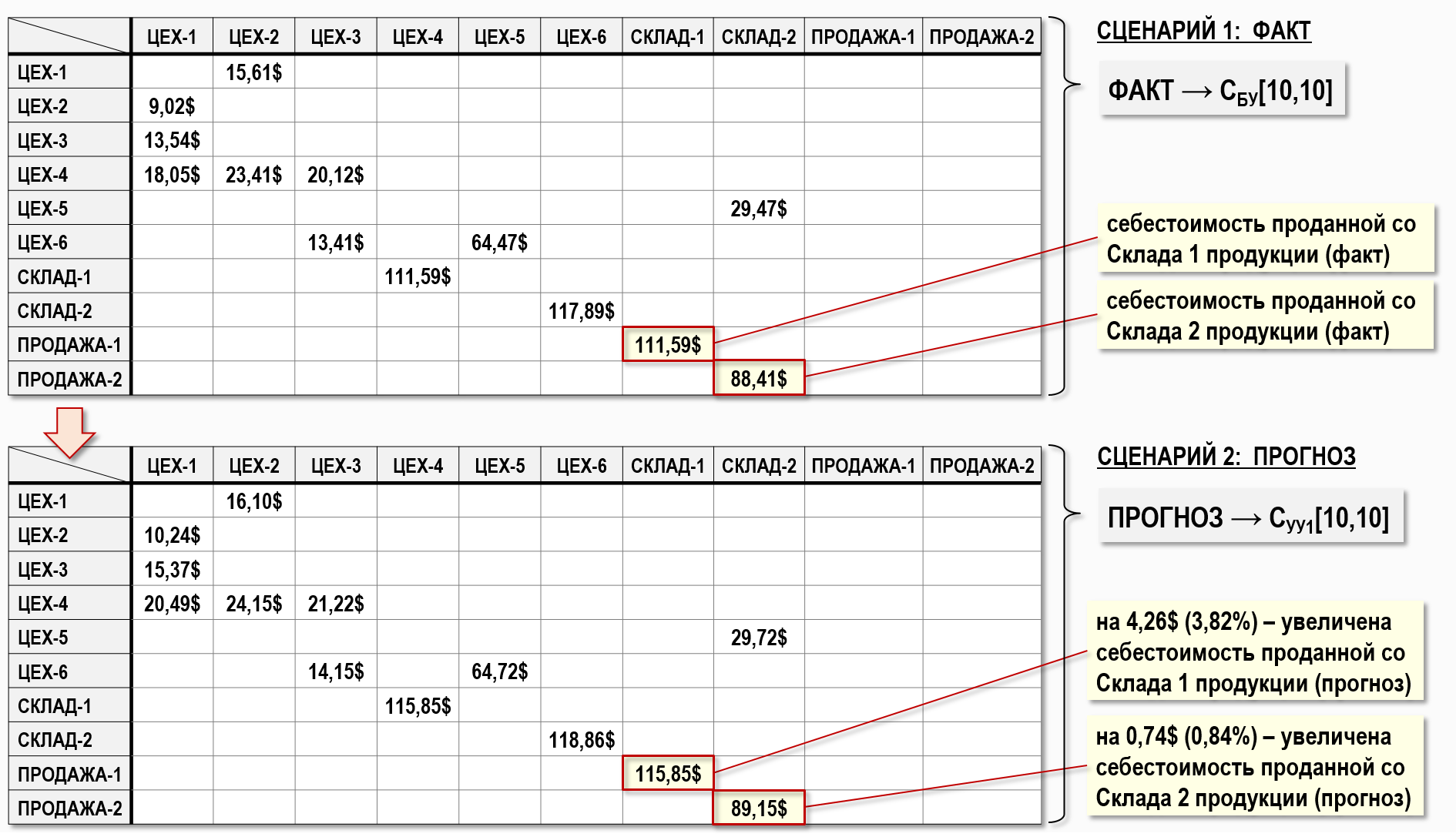
Решив СЛАУ, представленные обеими расширенными матрицами исходных коэффициентов, найдем фактические и прогнозные значения тарифов и определим стоимости вторичных затрат для Сценария 1 и Сценария 2, которые представим с помощью соответствующих матриц стоимостей CБУ[10,10] и CУУ1[10,10].
Таким образом, имея в своем распоряжении Граф затрат предыдущего периода, мы легко можем рассчитать прогнозные значения себестоимости для следующего периода при увеличении стоимости первичных затрат Цеха-1 на 20%. Для этого надо всего лишь изменить значение элемента на пересечении первой строки и правого столбца в расширенной матрице исходных коэффициентов и решить полученную СЛАУ.
Осталось только определиться, куда можно поместить результаты данного расчета? Ведь эти прогнозные значения не должны попасть в финансовую отчетность предприятия, а значит они не должны отражаться в бухгалтерском учете. Этот вопрос легко решить, например, добавив в журнал хозяйственных операций столбец «СЛОЙ», в котором с помощью разделителя учета определяется тот вид (слой) учета, к которому относятся учетные данные. В результате мы получим хранилище учетных данных, разделенное на непересекающиеся между собой области учетных данных (слои) значениями разделителя учета.
Для расчета фактической себестоимости мы использовали слой БУ – бухгалтерского учета. Для расчета прогнозных значений себестоимости был использован слой УУ1 – первый слой управленческого учета. Понятно, что можно ввести еще сколь угодно много других слоев управленческого или налогового учета и решать в них свои задачи, а структуру Графа затрат можно, например, просто импортировать в выбранные слои учета и при необходимости отредактировать.
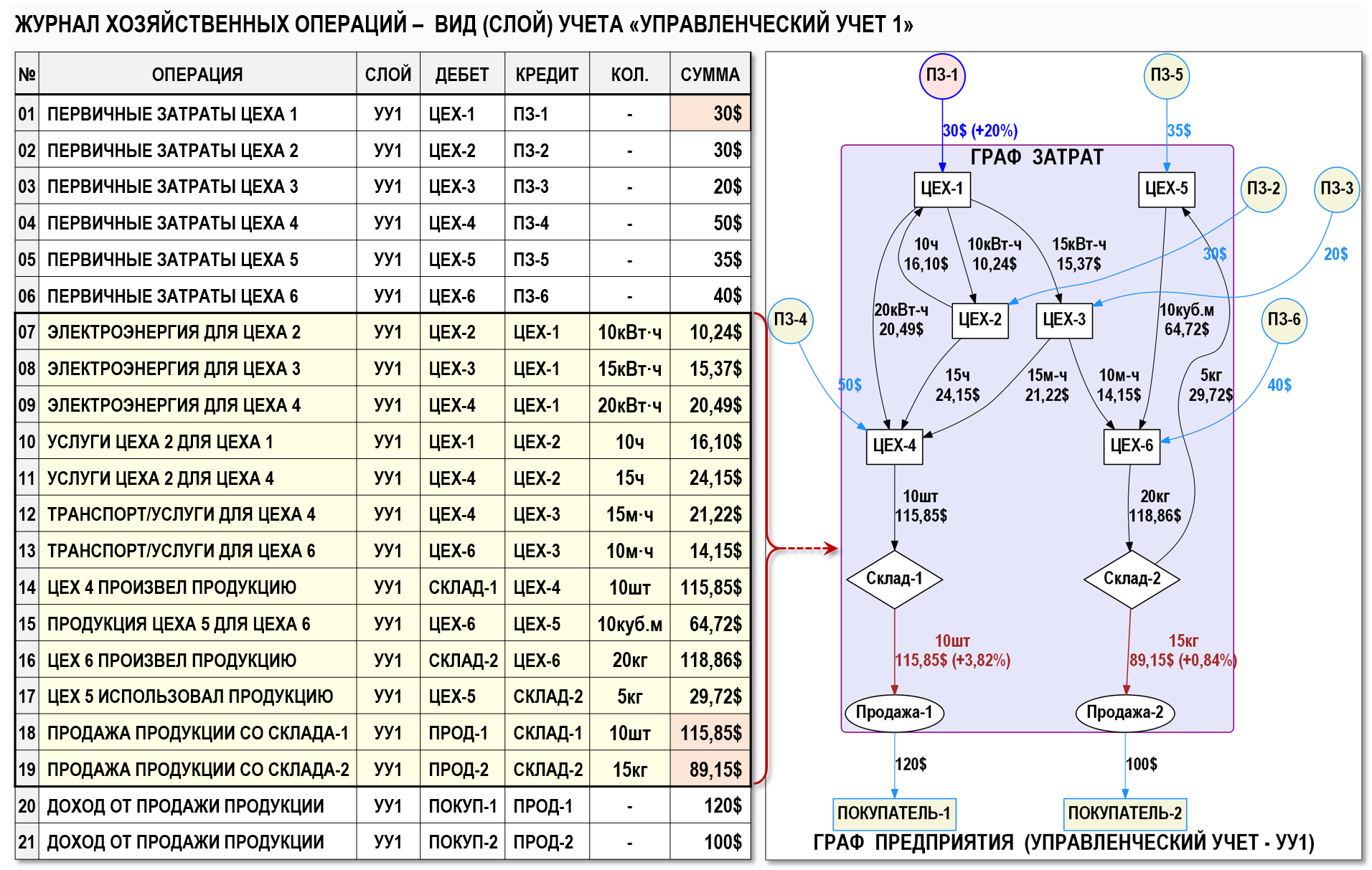
Внесем полученные значения в ЖХО для слоя учета УУ1 и представим Граф затрат в графической форме.
Определим прогнозные финансовые результаты для каждого вида деятельности:
ProfitУУ1-1=120$–115,85$=4,15$ (прибыль от продажи продукции со Склада-1)
ProfitУУ1-2=100$–89,15$=10,85$ (прибыль от продажи продукции со Склада-2)
ProfitУУ1=4,15$+10,85$=15$ (общая прибыль от продажи продукции)
Таким образом, проведенные на Графе затрат расчеты показывают, что в результате увеличения на 20% стоимости потребляемого Цехом-1 дизельного топлива себестоимость проданной продукции должна увеличиться на:
115,85$–111,59$=4,26$ (3,82%) (продукция со Склада-1)
89,15$–88,41$=0,74$ (0,84%) (продукция со Склада-2)
а прибыль от продажи продукции должна уменьшиться на:
ProfitБУ1–ProfitУУ1-1=8,41$–4,15$=4,26$ (50,65%) (продукция со Склада-1)
ProfitБУ2–ProfitУУ1-2=11,59$–10,85$=0,74$ (6,38%) (продукция со Склада-2)
ProfitБУ–ProfitУУ1=20$–15$=5$ (25%) (оба вида продукции)
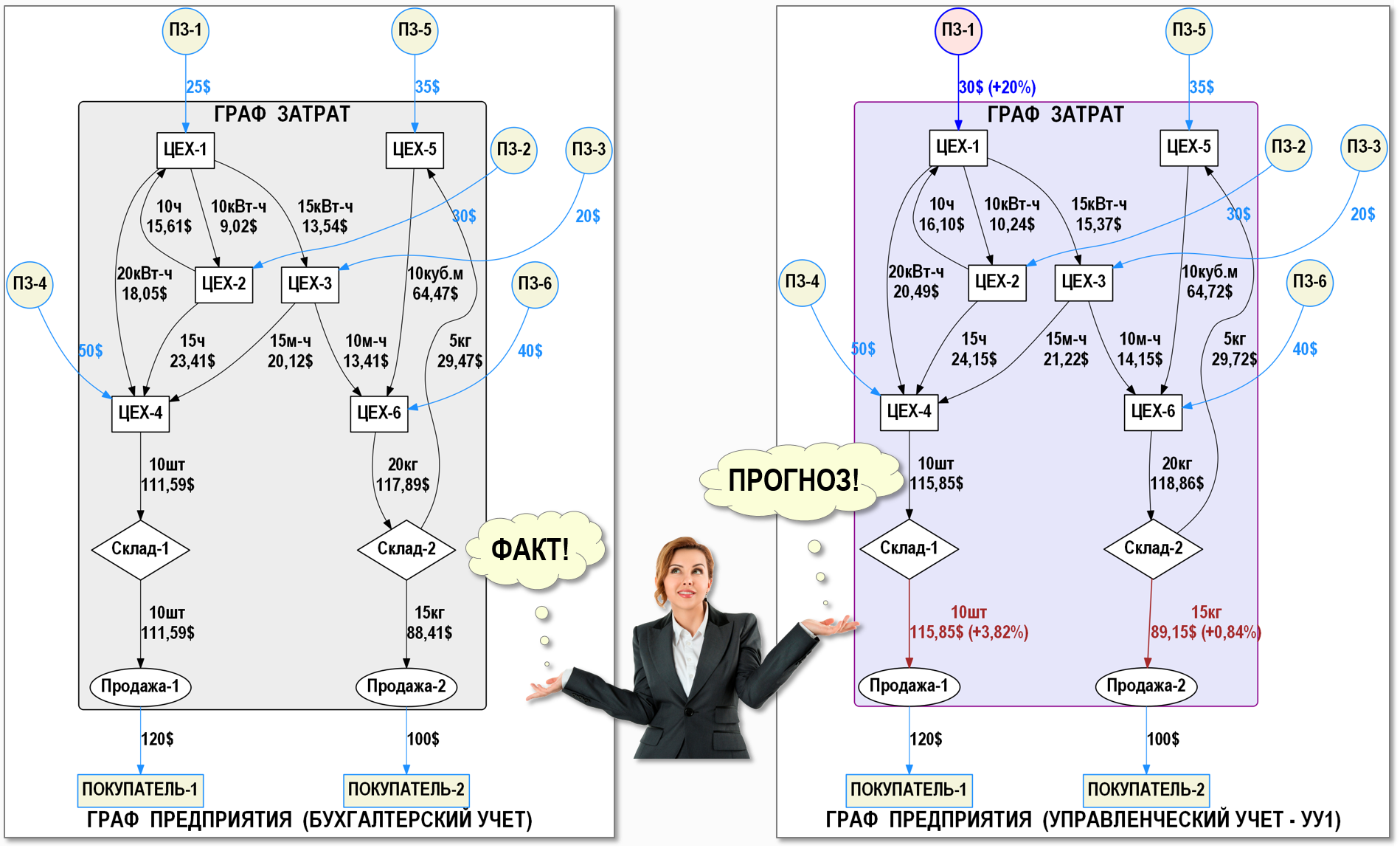
Расположим для наглядности оба Графа затрат рядом, чтобы увидеть также, как изменятся стоимости всех вторичных затрат при увеличении стоимости первичных затрат Цеха-1 на 5$.
Какие выводы можно сделать из рассмотренной в данной статье задачи, имея в виду не конкретные результаты ее решения, а примененную для этого технологию ее решения?
Во-первых, технология расчета себестоимости на Графе затрат инвариантна к виду учета, т.е. для Графа затрат не имеет никакого значения, откуда поступили первичные данные для расчета себестоимости – из бухгалтерского, налогового или управленческого учета. Расчет себестоимости в любом случае будет произведен по одной и той же технологии, что очень удобно для автоматизации.
Во-вторых, расчет прогнозных значений себестоимости производится не с помощью каких-то очень приближенных «общих» формул, а с помощью максимально подробной модели хозяйственных процессов, какая только может быть в распоряжении аналитика – на основе модели, в данном случае взятой из бухгалтерского учета. Именно поэтому так легко и наглядно происходит сравнение фактических и прогнозных значений себестоимости.
И в-третьих, использование многослойного Графа затрат предоставляет широчайшие возможности для анализа в отдельных слоях управленческого учета всевозможных сценариев производственной программы предприятия, т.к. у аналитика появляется возможность работать со своим многослойным хранилищем учетных данных, в котором нет никаких принципиальных ограничений на число используемых слоев учета.
В следующей статье мы еще более увеличим аналитические возможности Графа затрат и рассмотрим, каким образом можно анализировать не только стоимости общих потоков вторичных затрат, как в рассмотренном примере, но также, используя элементы затрат, проводить анализ влияния на себестоимость, например, отдельных статей бюджетов затрат цехов или отдельных групп статей этих бюджетов затрат, т.е. проводить анализ структуры стоимости потоков вторичных затрат.
Вступайте в нашу телеграмм-группу Инфостарт