Вводная часть
Перед тем, как перейти непосредственно к теме статьи, имеет смысл кратко напомнить несколько ключевых моментов, связанных с расчетом себестоимости в системах бухгалтерского учета, основанных на использовании счетов учета и двойной записи. Задача расчета себестоимости (процедура закрытия затрат периода) в таких системах учета всегда сводится к решению систем линейных алгебраических уравнений (СЛАУ). Это объясняется тем, что в системе бухгалтерского учета используются счета учета затрат, для каждого из которых должно выполняться свое балансовое уравнение (см. Балансовые уравнения в Графе затрат). Счетов учета затрат, а значит и балансовых уравнений много, и все уравнения должны выполняться одновременно. Это и называется системой уравнений, в нашем случае – СЛАУ, которую нужно решить при закрытии затрат периода. Проще говоря, если учетная технология предполагает использование счетов учета, то она обязана обеспечить выполнение их балансовых уравнений, что и происходит в результате решения СЛАУ. В настоящее время существует достаточное число численных методов решения таких систем уравнений, так что каких-то особых проблем такая задача вроде бы вызывать не должна. Это первое, о чем хотелось бы напомнить.
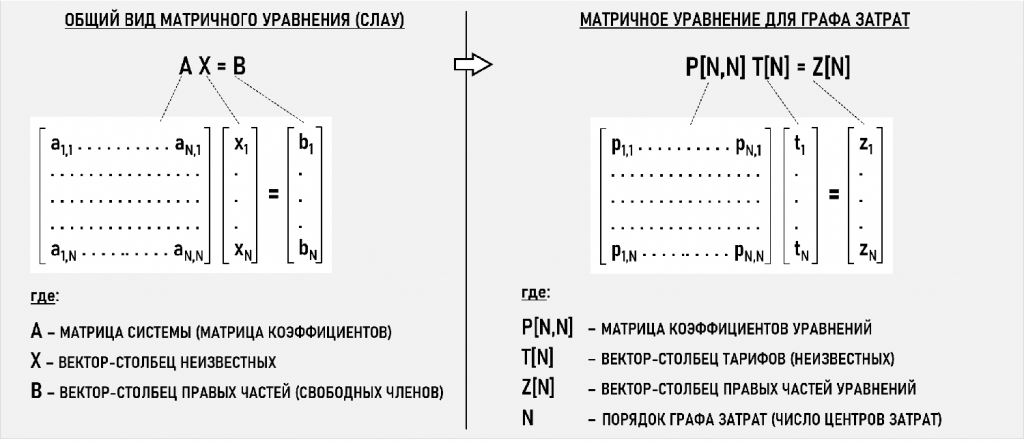
Второй важный момент заключается в том, что счетов учета затрат может быть очень много и СЛАУ могут иметь большую и даже сверхбольшую размерность, что серьезно усложняет осознанную работу с ними, особенно если СЛАУ представлены в скалярном виде (в виде множества строк, содержащих уравнения). Можно ли сделать работу пользователя со СЛАУ более технологичной, то есть не очень сложной и экономичной по времени, а заключенный в СЛАУ экономический смысл более прозрачным? Да, можно, воспользовавшись матричной формой записи СЛАУ (см. Матричная форма записи СЛАУ для Графа затрат). Ниже на рисунке представлен принятый в линейной алгебре общий вид СЛАУ в матричной форме (матричное уравнение), а также «интерпретация» матричного уравнения для Графа затрат с учетом терминологии теории Графов затрат, предполагающей собственные названия матриц:
Напомним, какие матрицы входят в матричное уравнение для Графа затрат:
P[N,N] – матрица коэффициентов уравнений, значения ее элементов известны до начала решения СЛАУ и определяются количествами единиц калькуляции, которыми обменялись центры затрат в рассматриваемом периоде. Данная матрица строится на основе таблицы, часто называемой «шахматкой», куда заносятся количества материалов, продукции, услуг и т.п., которыми обменялись подразделения предприятия в рассматриваемом периоде
T[N] – вектор-столбец тарифов, где тариф – стоимость одной единицы калькуляции. Поиск значений тарифов является целью решения СЛАУ, перемножив тарифы и количества единиц калькуляции получим искомые стоимости потоков затрат в Графе затрат
Z[N] – вектор-столбец правых частей уравнений, значения его элементов известны до начала решения СЛАУ и определяются на основе стоимости первичных затрат и затрат в незавершенном производстве
Для иллюстрации того, насколько работа пользователя с матричными уравнениями может быть технологична и прозрачна с точки зрения экономического смысла, рассмотрим, как это может выглядеть на практике. Целью данного иллюстративного примера является скорее показать визуальный образ инструментария, который может быть доступен пользователю учетной системы, чем рассмотреть тонкости его математической «начинки».
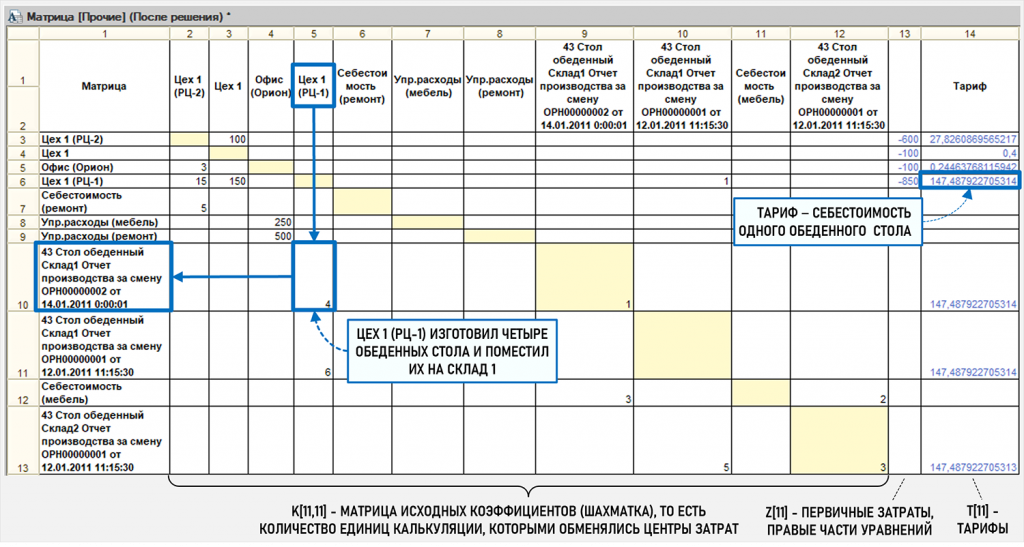
На рисунке представлен визуальный образ матричного уравнения в виде таблицы, в которой есть столбцы тарифов T[11] и правых частей уравнений Z[11], только вместо матрицы коэффициентов уравнений P[11,11] показана матрица исходных коэффициентов K[11,11], которая просто более удобна для практической работы, но содержит все данные, необходимые для формирования матрицы P[11,11] (см. Матричная форма записи СЛАУ для Графа затрат), обе матрицы отличаются только элементами на главной диагонали. Можно сказать, что матрица исходных коэффициентов K[11,11] является инструментом пользователя, а сформированная на ее основе матрица коэффициентов уравнений P[11,11] нужна для решения технических вопросов – для решения СЛАУ.
Например, в таблице легко увидеть, что центр затрат Цех1(РЦ-1) изготовил 14 января четыре обеденных стола и поместил их на Склад1, а себестоимость одного стола (тариф) составила 147,49 руб. Как видим, работа с матричным уравнением не представляет каких-либо сложностей, все довольно наглядно и компактно. Но это при условии, когда пользователю не нужно «ломать голову» над тонкостями процедуры численного решения СЛАУ, это все-таки зона ответственности разработчиков системы. Попутно также отметим, что даже в такой маленькой матрице K[11,11] число ненулевых элементов достаточно мало, то есть эту матрицу можно считать разреженной, в реальных матрицах число ненулевых элементов обычно составляет буквально единицы процентов.
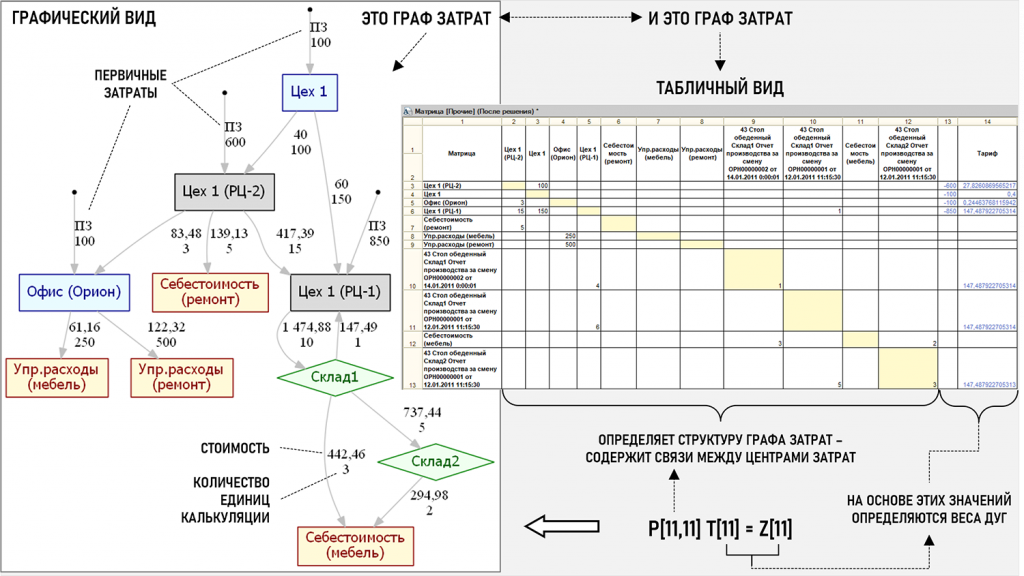
Посмотрим визуальный образ еще одного полезного инструмента, позволяющего представить показанную выше таблицу, а фактически – матричное уравнение, в графическом виде. Можно назвать этот инструмент интерактивной подсистемой визуализации Графа затрат. Сразу уточним, что некорректно говорить о том, что эта подсистема представляет данные из таблицы в виде графа (в нашем случае – Графа затрат), поскольку граф является «самостоятельным» математическим объектом и в зависимости от особенностей решаемой задачи может быть представлен как в табличной, так и в графической форме. Подобный функционал учетной системы полезен при анализе сложных структур потоков затрат, тем более если интерактивная подсистема визуализации позволяет выделять отдельные фрагменты Графа затрат и изучать потоки затрат в них в разном масштабе, как на интерактивных географических картах.
Матрица исходных коэффициентов K[11,11] определяет топологическую структуру Графа затрат, поскольку именно эта матрица содержит связи между центрами затрат (двойная запись), а матрицы правых частей уравнений Z[11] и тарифов T[11] отвечают за формирование значений весов дуг – верхнее число показывает стоимость потока затрат, а нижнее число – количество единиц калькуляции. В данном конкретном примере правда в графическом виде показано не 11, а 10 центров затрат, поскольку для наглядности два центра затрат для Склада1 были объединены в один, что лишний раз подчеркивает интерактивные возможности подсистемы визуализации.
Таким образом, в системах бухгалтерского учета, основанных на использовании счетов учета и двойной записи, задачу расчета себестоимости всегда можно свести к решению матричного уравнения P[N,N]T[N]=Z[N], причем решать его желательно численным методом, оптимизированным для работы с разреженными матрицами P[N,N]. При наличии соответствующего функционала системы работа с матричным уравнением не представляет особых сложностей для пользователя, а трудоемкость процедуры решения СЛАУ на практике обычно связана только со сбором из системы учета значений элементов матриц P[N,N] и Z[N]. Вот, собственно, и весь алгоритм расчета себестоимости, если его выделить из весьма объемной бухгалтерской «беллетристики» на тему расчета себестоимости. Казалось бы, что тут еще обсуждать? Оказывается, есть интересные моменты.
Говорят, что в среде математиков и физиков раньше было популярно мнение о том, что уравнения любят, чтобы их разглядывали (может и сейчас еще популярно). У нас есть матричное уравнение для расчета себестоимости, попробуем к нему присмотреться внимательнее и понять, какие еще задачи можно решать с его помощью.
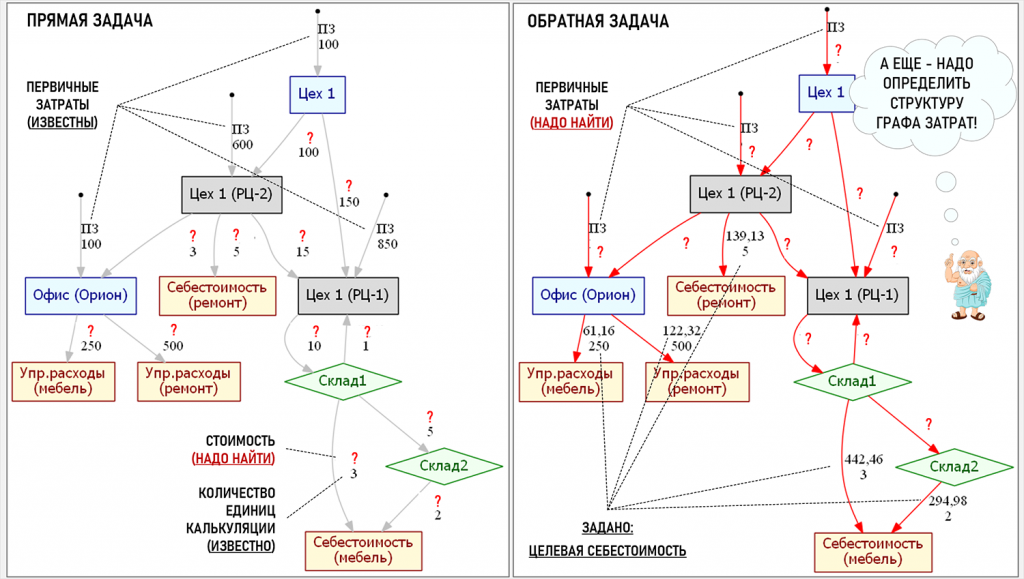
Прямые и обратные задачи на Графах затрат
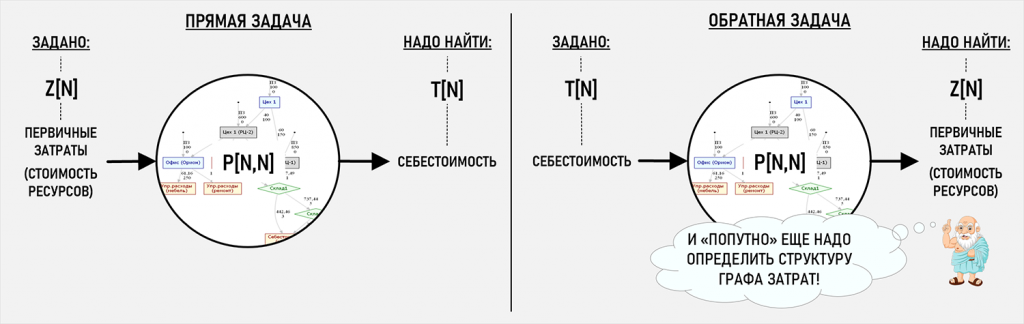
Первый вывод из «разглядывания» матричного уравнения очевиден – если заранее известны значения элементов P[N,N] и Z[N], а неизвестными являются значения элементов T[N], то это обычная задача расчета себестоимости произведенной и проданной продукции (работ, услуг). Такую задачу можно отнести к классу прямых задач, решение которых в общем случае связано с отысканием следствия какого-либо процесса по известной причине. В нашем случае известны стоимости первичных затрат и количества единиц калькуляции, которыми обменялись центры затрат – это причины. На основе этих данных матричное уравнение позволяет единственным образом определить значения тарифов (а значит и себестоимость) – это следствие.
Здесь имеет смысл напомнить о том, что с точки зрения пары философских категорий причина и следствие задачи математического моделирования условно можно разделить на два класса – прямые и обратные задачи. Этими категориями обозначается связь между явлениями, когда одно из них – причина вызывает (порождает) другое явление – следствие, причем эта связь является однонаправленной от причины к следствию. В прямых задачах при известных причинах требуется определить следствия, а обратные задачи пытаются определить причины, приведшие к тем или иным следствиям.
Теперь представим, что нам известны значения элементов P[N,N] и T[N], а нужно найти значения элементов Z[N]. Мы имеем полное право рассмотреть и такой вариант, ведь матричное уравнение позволяет это сделать. В чем экономический смысл такой задачи? Мы задаем целевые значения себестоимости и определяем стоимости первичных затрат, при которых это происходит. Эту задачу можно отнести к классу обратных задач, когда известен результат (целевая себестоимость), и нужно определить при каких исходных параметрах он может быть получен. Например, метод target costing предполагает, что сначала задается целевая себестоимость изделия, а точнее цена его возможной реализации за вычетом желаемой величины прибыли, а затем сотрудники компании пытаются спроектировать и изготовить изделие с заданными параметрами и целевой себестоимостью. Это типичная обратная задача.
Казалось бы, все просто, задаем целевые значения себестоимости и с помощью матричного уравнения определяем необходимые для этого стоимости первичных затрат. Но это только на первый взгляд. На самом деле, в отличие от прямых задач, трудности решения обратных задач связаны с тем, что они относятся к классу некорректно поставленных задач, то есть задач, которые, во-первых, просто могут не иметь решения, во-вторых, решений может быть не одно, а целое множество, и, в-третьих, небольшие отклонения в данных могут вызывать значительные отклонения результатов решения (неустойчивость решения). Для корректно поставленных задач должны выполняться три условия корректности по Адамару – у математической задачи решение должно существовать, быть единственным и непрерывно зависеть от исходных данных. Если хотя бы одно из условий нарушается, то задачу относят к классу некорректно поставленных задач.
В контексте нашей темы можно сказать, что по-существу многие задачи экономического планирования относятся к классу обратных, а значит некорректно поставленных задач, когда задается желаемый к получению ассортимент продукции и его целевая себестоимость (следствие) и требуется определить каким образом этого можно достичь (причина). Вполне возможно, что в текущих условиях рынка эта задача вообще не будет иметь решения, или можно произвести продукцию используя разные варианты производственных процессов (множество решений). В конце концов можно и купить эту продукцию (или ее отдельные части) у контрагентов для последующей перепродажи покупателям или для использования в собственных производственных процессах. Это значит, что для решения такой задачи нужна дополнительная информация, которая поможет выделить предполагаемую область возможных решений, где и будет происходить поиск их точных или приближенных значений. С точки зрения математической модели это означает, что в зависимости от дополнительной информации одну и ту же целевую себестоимость можно получить с помощью разных вариантов матриц P[N,N] и Z[N], то есть обратная задача сводится к нахождению оптимальных вариантов этих матриц.
Выводы
Любая система бухгалтерского учета должна удовлетворять требованию рациональности (ПБУ 1/2008), что предполагает умение бухгалтера мыслить рационально. А что это такое – мыслить рационально? Это значит, что решать учетные задачи бухгалтер должен на основе мышления и логики, фактов и объективных данных. Это позволяет непредвзято оценивать хозяйственные ситуации, избегать эмоциональных и субъективных ошибок в их оценке. Что значит принимать решения на основе логики? Это значит использовать в мыслительном процессе логические конструкции и понятия. Например:
- функционирование большинства систем бухгалтерского учета основано на применении счетов учета и двойной записи – это факт (true)
- для всех счетов учета должны выполняться балансовые уравнения – это факт (true)
- балансовые уравнения для счетов учета затрат классифицируются как линейные алгебраические уравнения – это факт (true)
- если эти уравнения должны одновременно выполняться для всех счетов учета затрат, то множество этих уравнений представляет собой СЛАУ – это факт (true)
Если обобщить все эти логические высказывания, то можно утверждать, что если система бухгалтерского учета основана на применении счетов учета и двойной записи, то процедура расчета себестоимости в такой системе всегда производится на основе решения СЛАУ, а так называемые разные способы закрытия затрат являются всего лишь попыткой создать особые бухгалтерские алгоритмы решения СЛАУ (см. Способы распределения затрат – прямой, пошаговый и с помощью СЛАУ). Осознание этого факта позволяет не только упорядочить и стандартизировать «обычную» процедуру расчета фактической себестоимости (закрытия затрат периода), но и получить ряд полезных бонусов в части решения других не менее важных учетных задач.
Во-первых, представление СЛАУ в матричной форме позволяет учетным специалистам работать с компактными и понятными объектами – матрицами, входящими в матричное уравнение для расчета себестоимости.
Во-вторых, матричное уравнение можно использовать для решения как прямых, так и обратных задач. К классу прямых задач можно отнести как задачу расчета фактической себестоимости, так и задачи расчета любых альтернативных значений себестоимости (например, прогнозных), поскольку алгоритм решения матричного уравнения в этих случаях полностью идентичен, а экономическим смыслом результаты расчета наполняет сам учетный специалист.
К классу обратных задач можно отнести задачу определения стоимости первичных затрат, необходимых для получения заданной целевой себестоимости. В данном случае необходимо найти значения элементов Z[N] при заданных значениях элементов P[N,N] и T[N]. Это весьма интересный и непростой класс задач, поскольку один и тот же результат здесь можно получить при различных исходных параметрах, поэтому важно иметь дополнительную информацию, например, о хозяйственных процессах на предприятии и их возможной корректировки для решения данной задачи. На взгляд автора это чрезвычайно перспективное направление развития учетной мысли, поскольку в результате можно получить достаточную степень формализации многих задач экономического анализа, прогнозирования и т.п., а использование матричного уравнения позволяет перейти от «текстовых» рассуждений на тему получения целевой себестоимости в плоскость «конкретных» численных экспериментов.
Вступайте в нашу телеграмм-группу Инфостарт