Муравьиный алгоритм в 1С для поиска оптимального маршрута

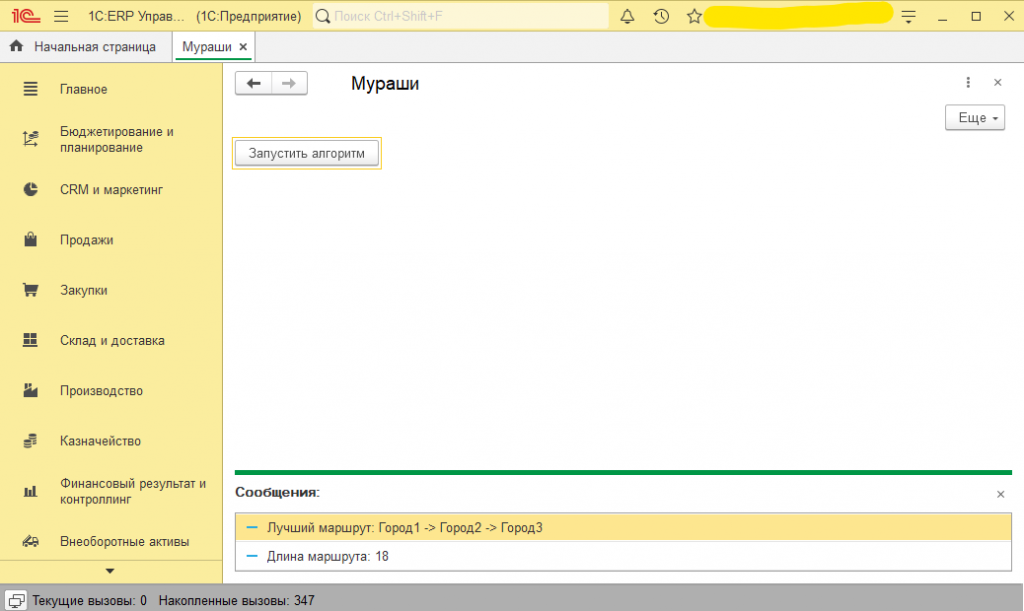
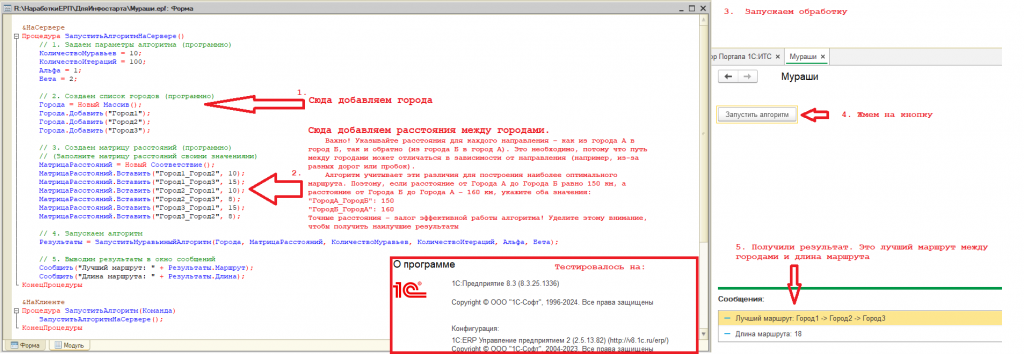
Внимание, на скриншоте пошаговая инструкция, куда добавлять данные при проверке. На примере добавил 3 города и расстояния между ними. Обработка должна работать в любой базе на платформе 1с v8.3, так как все процедуры и функции свои, тестировалось в 1С:ERP Управление предприятием 2 (2.5.13.82)  

В мире 1С-разработки часто возникают задачи, требующие оптимизации: распределение ресурсов, планирование производства и, конечно же, оптимизация маршрутов. Существуют различные алгоритмы для решения этих задач, и один из самых интересных и эффективных – муравьиный алгоритм. Этот алгоритм, вдохновленный поведением муравьиной колонии, позволяет находить оптимальные или близкие к оптимальным решения для сложных задач. В этой статье мы простым языком расскажем, что такое муравьиный алгоритм, как его можно применить в 1С и представим практическую реализацию для оптимизации маршрутов.

Муравьиный алгоритм (Ant Colony Optimization, ACO) – это метаэвристический алгоритм, вдохновленный поведением муравьиной колонии при поиске кратчайшего пути от муравейника к источнику пищи. Муравьи, двигаясь в поисках пищи, оставляют на своем пути феромоны – специальные вещества, которые служат ориентиром для других муравьев. Чем больше муравьев пройдет по определенному пути, тем больше феромонов на нем останется, и тем привлекательнее он станет для других муравьев. В результате, большинство муравьев в колонии выбирают кратчайший путь, на котором накопилось больше всего феромонов.

Основные принципы муравьиного алгоритма:

• Муравьи: Агенты, которые ищут решение задачи.
• Феромоны: Информация, которая остается на пути муравьев и влияет на выбор других муравьев.
• Испарение феромонов: Феромоны со временем испаряются, что позволяет алгоритму “забывать” неоптимальные пути и исследовать новые варианты.
• Эвристическая информация: Дополнительная информация о задаче, которая помогает муравьям принимать более обоснованные решения (например, расстояние между городами при оптимизации маршрутов).

Муравьиный алгоритм применяется для решения различных задач оптимизации, таких как:

• Задача коммивояжера (TSP): Поиск кратчайшего маршрута, проходящего через все заданные города по одному разу.
• Задача маршрутизации транспорта (VRP): Оптимизация маршрутов для нескольких транспортных средств, доставляющих товары клиентам.
• Задачи планирования и расписания: Оптимизация последовательности выполнения задач, распределение ресурсов и т.д.
• Задачи кластеризации и классификации: Группировка данных по определенным признакам.

    Применение муравьиного алгоритма в 1С может быть полезным для решения задач, связанных с логистикой, доставкой, обслуживанием клиентов и т.д. Например, можно оптимизировать маршруты курьеров, торговых представителей, сервисных инженеров, чтобы сократить время на дорогу, снизить затраты на топливо и повысить эффективность работы.

Для реализации муравьиного алгоритма в 1С необходимо:

1. Представить задачу в виде графа: Города или точки доставки – это вершины графа, а расстояния между ними – ребра графа.
2. Создать структуру для хранения информации о феромонах: В 1С можно использовать структуру или соответствие для хранения информации о количестве феромонов на каждом ребре графа.
3. Реализовать функции для:
   • Построения маршрута муравья: Функция должна выбирать следующий город для посещения на основе информации о феромонах и эвристической информации (расстоянии).
   • Расчета длины маршрута: Функция должна вычислять общую длину маршрута, пройденного муравьем.
   • Обновления феромонов: Функция должна изменять количество феромонов на ребрах графа в зависимости от качества маршрутов, пройденных муравьями.
4. Запустить алгоритм на определенное количество итераций: На каждой итерации муравьи строят новые маршруты, обновляют феромоны, и алгоритм сходится к оптимальному решению.

&НаСервере
Функция ПостроитьМаршрутМуравья(Города, МатрицаРасстояний, Альфа, Бета)

    Маршрут = Новый Массив();
    НепосещенныеГорода = Новый Массив();
    Для Каждого Город Из Города Цикл
        НепосещенныеГорода.Добавить(Город);
    КонецЦикла;

    // Выбираем начальный город случайным образом
    ГСЧ = Новый ГенераторСлучайныхЧисел();
    ИндексНачальногоГорода = Цел(ГСЧ.СлучайноеЧисло(0, НепосещенныеГорода.Количество() - 1));
    НачальныйГород = НепосещенныеГорода[ИндексНачальногоГорода];
    Маршрут.Добавить(НачальныйГород);
    НепосещенныеГорода.Удалить(ИндексНачальногоГорода);

    // Строим маршрут, пока есть непосещенные города
    Пока НепосещенныеГорода.Количество() > 0 Цикл
        СледующийГород = ВыбратьСледующийГород(Маршрут[Маршрут.Количество() - 1], НепосещенныеГорода, МатрицаРасстояний, Альфа, Бета);
        Маршрут.Добавить(СледующийГород);
        НепосещенныеГорода.Удалить(НепосещенныеГорода.Найти(СледующийГород));
    КонецЦикла;

    Возврат Маршрут;

КонецФункции

Этот код создает массив с маршрутом муравья, выбирая каждый раз лучший город (с точки зрения расстояния) из непосещенных.

Рассмотрим реализацию ключевой функции алгоритма - выбора следующего города для посещения муравьем.

Функция ВыбратьСледующийГород играет центральную роль в построении маршрута муравья. Именно в этой функции определяется, какой город будет следующим в маршруте. В нашей упрощенной реализации, представленной ниже, выбор следующего города основывается исключительно на расстоянии до него:

&НаСервере
Функция ВыбратьСледующийГород(ТекущийГород, НепосещенныеГорода, МатрицаРасстояний, Альфа, Бета)

    // Выбираем следующий город с учетом расстояния
    ЛучшийГород = "";
    ЛучшееРасстояние = -1;

    Для Каждого Город Из НепосещенныеГорода Цикл
        Ключ = ТекущийГород + "_" + Город;
        Расстояние = МатрицаРасстояний[Ключ];

        Если ЛучшийГород = "" ИЛИ Расстояние < ЛучшееРасстояние Тогда
            ЛучшийГород = Город;
            ЛучшееРасстояние = Расстояние;
        КонецЕсли;
    КонецЦикла;

    Возврат ЛучшийГород;

КонецФункции

Этот код прост и понятен: он перебирает все непосещенные города и выбирает тот, расстояние до которого минимально. В более сложных реализациях этой функции можно учитывать также информацию о феромонах и другие факторы, влияющие на выбор муравья. Параметры Альфа и Бета, хотя и передаются в функцию, в данной реализации не используются, но их можно задействовать для настройки влияния феромонов и расстояния на выбор города.

Описание реализации функции, рассчитывающей общую длину маршрута на основе матрицы расстояний: После того, как муравей построил свой маршрут, необходимо оценить его качество. Для этого используется функция РассчитатьДлинуМаршрута, которая вычисляет общую длину маршрута, суммируя расстояния между последовательными городами в маршруте:

&НаСервере
Функция РассчитатьДлинуМаршрута(Маршрут, МатрицаРасстояний)

    Длина = 0;
    Для Индекс = 1 По Маршрут.Количество() - 1 Цикл
        Город1 = Маршрут[Индекс - 1];
        Город2 = Маршрут[Индекс];
        Ключ = Город1 + "_" + Город2;
        Длина = Длина + МатрицаРасстояний[Ключ];
    КонецЦикла;

    Возврат Длина;

КонецФункции 

Эта функция перебирает все пары соседних городов в маршруте, находит расстояние между ними в матрице расстояний и добавляет его к общей длине маршрута. Результатом работы функции является числовое значение, представляющее собой общую длину маршрута.

Функция ЗапуститьМуравьиныйАлгоритм является основной функцией, которая координирует работу всех остальных функций и реализует логику муравьиного алгоритма:

&НаСервере
Функция ЗапуститьМуравьиныйАлгоритм(Города, МатрицаРасстояний, КоличествоМуравьев, КоличествоИтераций, Альфа, Бета)

    // 1. Инициализация
    ЛучшийМаршрут = "";
    ЛучшаяДлина = 0;

    // 2. Основной цикл алгоритма
    Для Итерация = 1 По КоличествоИтераций Цикл

        // a) Создаем муравьев и строим их маршруты
        МаршрутыМуравьев = Новый Массив();
        Для Муравей = 1 По КоличествоМуравьев Цикл
            Маршрут = ПостроитьМаршрутМуравья(Города, МатрицаРасстояний, Альфа, Бета);
            МаршрутыМуравьев.Добавить(Маршрут);
        КонецЦикла;

        // b) Оцениваем маршруты муравьев и выбираем лучший
        Для Каждого Маршрут Из МаршрутыМуравьев Цикл
            ДлинаМаршрута = РассчитатьДлинуМаршрута(Маршрут, МатрицаРасстояний);

            Если ЛучшийМаршрут = "" ИЛИ ДлинаМаршрута < ЛучшаяДлина Тогда
                ЛучшийМаршрут = СтрСоединить(Маршрут, " -> ");
                ЛучшаяДлина = ДлинаМаршрута;
            КонецЕсли;
        КонецЦикла;

        // (В этой упрощенной версии мы не обновляем феромоны)

    КонецЦикла;

    // 3. Возвращаем результаты
    Результаты = Новый Структура("Маршрут, Длина", ЛучшийМаршрут, ЛучшаяДлина);
    Возврат Результаты;

КонецФункции

В этой функции происходит инициализация переменных, запуск основного цикла алгоритма, создание муравьев и построение их маршрутов, оценка маршрутов и выбор лучшего маршрута. В данной упрощенной версии мы не реализуем обновление феромонов, что значительно упрощает алгоритм, но снижает его эффективность. Для повышения эффективности алгоритма необходимо реализовать обновление феромонов на основе качества построенных маршрутов.

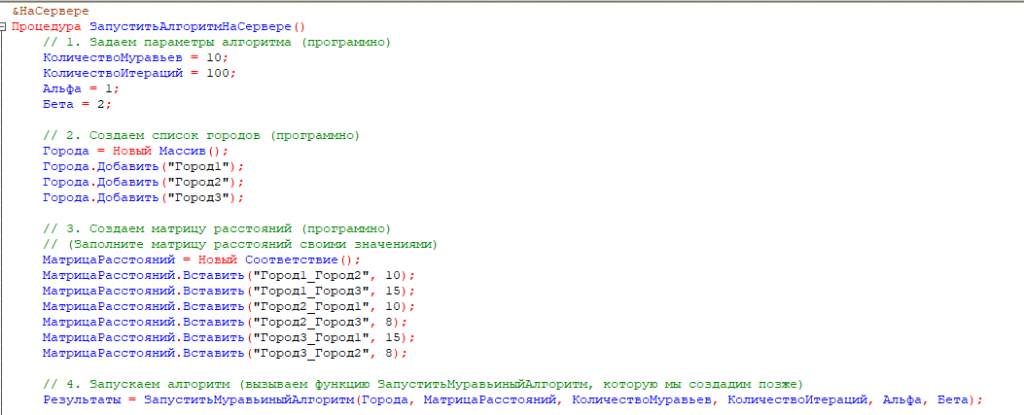
Основные данные для алгоритма вызовем при создании обработки:

&НаСервере
Процедура ЗапуститьАлгоритмНаСервере()
	// 1. Задаем параметры алгоритма (программно)
    КоличествоМуравьев = 10;
    КоличествоИтераций = 100;
    Альфа = 1;
    Бета = 2;

    // 2. Создаем список городов (программно)
    Города = Новый Массив();
    Города.Добавить("Город1");
    Города.Добавить("Город2");
    Города.Добавить("Город3");

    // 3. Создаем матрицу расстояний (программно)
    // (Заполните матрицу расстояний своими значениями)
    МатрицаРасстояний = Новый Соответствие();
    МатрицаРасстояний.Вставить("Город1_Город2", 10);
    МатрицаРасстояний.Вставить("Город1_Город3", 15);
    МатрицаРасстояний.Вставить("Город2_Город1", 10);
    МатрицаРасстояний.Вставить("Город2_Город3", 8);
    МатрицаРасстояний.Вставить("Город3_Город1", 15);
    МатрицаРасстояний.Вставить("Город3_Город2", 8);

    // 4. Запускаем алгоритм
    Результаты = ЗапуститьМуравьиныйАлгоритм(Города, МатрицаРасстояний, КоличествоМуравьев, КоличествоИтераций, Альфа, Бета);

    // 5. Выводим результаты в окно сообщений
    Сообщить("Лучший маршрут: " + Результаты.Маршрут);
    Сообщить("Длина маршрута: " + Результаты.Длина);
КонецПроцедуры

Представленная в этой статье реализация муравьиного алгоритма является упрощенной и служит, скорее, для демонстрации основных принципов работы алгоритма. Для получения более эффективных результатов и решения реальных задач необходимо внести ряд улучшений:

• Реализовать обновление феромонов: Добавить логику для изменения количества феромонов на ребрах графа в зависимости от качества маршрутов, пройденных муравьями. Это позволит алгоритму сходиться к более оптимальным решениям.
• Учитывать эвристическую информацию: В функции ВыбратьСледующийГород учитывать не только расстояние до следующего города, но и другие факторы, такие как стоимость доставки, время в пути и т.д.
• Использовать более сложные стратегии выбора следующего города: Вместо простого выбора города с минимальным расстоянием можно использовать вероятностные методы выбора, учитывающие как феромоны, так и эвристическую информацию.
• Настроить параметры алгоритма: Подобрать оптимальные значения параметров Альфа, Бета, КоличествоМуравьев, КоличествоИтераций для конкретной задачи.

Примеры практического применения муравьиного алгоритма в 1С:

• Оптимизация маршрутов курьеров: Алгоритм может помочь курьерской службе оптимально распределить заказы между курьерами и построить для них наиболее короткие маршруты, чтобы сократить время доставки и снизить затраты на топливо.
• Планирование посещений торговых представителей: Алгоритм может помочь торговым представителям оптимально спланировать свои визиты к клиентам, чтобы максимизировать количество посещений и увеличить объем продаж.
• Оптимизация маршрутов сервисных инженеров: Алгоритм может помочь сервисным компаниям оптимально распределить заявки между инженерами и построить для них наиболее короткие маршруты, чтобы сократить время реагирования на заявки и повысить уровень обслуживания клиентов.
• Оптимизация логистики на складе: Алгоритм может помочь оптимизировать перемещение товаров по складу, минимизируя расстояния и время на выполнение операций.

Муравьиный алгоритм – это мощный инструмент для решения задач оптимизации, который может быть успешно применен в 1С для решения различных задач, связанных с логистикой, доставкой и обслуживанием клиентов. Представленная в этой статье простая реализация алгоритма может стать отправной точкой для разработки более сложных и эффективных решений. Не бойтесь экспериментировать, настраивать параметры алгоритма и адаптировать его под свои конкретные задачи, и вы сможете получить значительный эффект от использования муравьиного алгоритма в своей 1С-системе.

20250401: Добавлена 2ая версия обработки (чуть сложнее первой, которая не учитывала феромоны и другие параметры, а лишь демонстрировала суть алгоритма и была легка к пониманию начинающим). Для загрузки доступны обе версии обработки.