Алгоритм Джонсона: Оптимизация последовательности обработки
Алгоритм Джонсона представляет собой элегантное и эффективное решение для классической задачи теории расписаний, а именно, для оптимизации последовательности выполнения задач на двух последовательных станках. Его основная цель – минимизировать общее время завершения всех работ (makespan), что напрямую влияет на повышение производительности и снижение издержек производства. Этот алгоритм, обладающий простотой реализации и высокой вычислительной эффективностью, нашел широкое применение в различных отраслях промышленности, где производственный процесс состоит из последовательных этапов.
Изучение истории возникновения алгоритма Джонсона открывает захватывающую перспективу в области исследования операций и теории расписаний. Разработанный Сельмером Джонсоном в 1954 году, этот алгоритм возник как решение конкретной производственной проблемы, связанной с оптимизацией последовательности обработки задач на двух станках. Формула алгоритма Джонсона, хотя и не выражена в виде сложных математических уравнений, базируется на простом и интуитивно понятном принципе: задачи с наименьшим временем обработки на первом станке следует выполнять в первую очередь, а задачи с наименьшим временем обработки на втором станке – в последнюю очередь. Этот принцип позволил Джонсону разработать алгоритм, который гарантированно находит оптимальное решение для данной задачи.
Суть алгоритма Джонсона заключается в следующем. Сначала необходимо определить наименьшее время обработки среди всех задач и станков. Если это время соответствует первому станку, то соответствующая задача ставится в начало последовательности. Если же это время соответствует второму станку, то задача ставится в конец последовательности. Далее эта задача исключается из рассмотрения, и процесс повторяется до тех пор, пока все задачи не будут упорядочены. Несмотря на свою простоту, алгоритм Джонсона обладает математической строгостью и гарантирует нахождение оптимального решения для задач, соответствующих его условиям. Эффективность алгоритма Джонсона обусловлена его способностью учитывать времена обработки задач на обоих станках и находить баланс между ними, минимизируя тем самым общее время завершения всех работ.
Практическое применение алгоритма Джонсона охватывает широкий спектр отраслей, включая машиностроение, химическую промышленность, пищевое производство и логистику. В машиностроении алгоритм может использоваться для оптимизации последовательности обработки деталей на двух последовательных станках. В химической промышленности – для оптимизации последовательности стадий процесса, таких как стадия подготовки сырья и линия упаковки. В логистике алгоритм может применяться для планирования последовательности обработки грузов на двух последовательных пунктах, таких как пункт приема и пункт отгрузки. В каждом из этих случаев алгоритм Джонсона позволяет повысить производительность, снизить издержки и улучшить организацию последовательности выполнения задач.
Сравнение алгоритма Джонсона с другими подходами позволяет выявить его сильные и слабые стороны, а также определить области его наиболее эффективного применения. Одним из наиболее распространенных методов является правило FIFO (First-In, First-Out), согласно которому задачи выполняются в порядке поступления. FIFO отличается простотой реализации, однако не учитывает времена обработки задач и, как следствие, может приводить к неоптимальным результатам. Другим распространенным методом является правило SPT (Shortest Processing Time), согласно которому задачи выполняются в порядке возрастания времени обработки. SPT минимизирует среднее время завершения задач, однако может приводить к увеличению времени выполнения наиболее длительных задач.
Алгоритм Джонсона, в отличие от FIFO и SPT, учитывает времена обработки задач на обоих станках и гарантирует нахождение оптимального решения для задач, соответствующих его условиям. Однако стоит отметить, что алгоритм Джонсона применим только к задачам с двумя станками, в то время как FIFO и SPT могут использоваться для задач с любым количеством станков. Для задач с более чем двумя станками существуют другие, более сложные методы, такие как генетические алгоритмы, имитация отжига и метод ветвей и границ. Эти методы имитация отжига, имитирующая процесс кристаллизации металлов, позволяют избегать локальных оптимумов и находить более глобальные решения, однако также требуют настройки параметров и могут быть вычислительно затратными. Метод ветвей и границ, основанный на систематическом переборе возможных решений, гарантирует для задач с двумя станками, где требуется быстрое и гарантированно оптимальное решение. Для более сложных задач следует рассматривать другие, более мощные, но и более ресурсоемкие методы.
Несмотря на наличие множества альтернативных подходов, алгоритм Джонсона продолжает оставаться актуальным и важной точкой для разработки более сложных алгоритмов и методов, учитывающих специфические особенности конкретных производственных систем.
Алгоритм Джонсона: Плюсы и минусы
Как и любой метод оптимизации, алгоритм Джонсона обладает своими сильными и слабыми сторонами, которые необходимо учитывать при его применении. К числу основных преимуществ алгоритма Джонсона следует отнести его простоту реализации. Алгоритм состоит из нескольких простых шагов, которые легко запрограммировать на любом языке программирования. Это делает его доступным для широкого круга пользователей, даже не имеющих глубоких знаний в области теории. Это означает, что если задача удовлетворяет требованиям алгоритма Джонсона, то полученное решение будет наилучшим из всех возможных.
Однако, алгоритм Джонсона имеет и ряд ограничений. Одним из основных недостатков является его применимость только к задачам с двумя станками. Это существенно ограничивает его использование в реальных производственных системах, где количество станков часто превышает два. Кроме того, алгоритм предполагает, что каждая задача должна быть обработана на обоих станках в одном и том же порядке. Это также может быть нереалистичным предположением, поскольку в некоторых производственных процессах задачи могут пропуска решение может быть неоптимальным. В таких случаях следует использовать другие, более сложные методы оптимизации.
Алгоритм Джонсона: Применение в 1С:Предприятие на живых примерах
Интеграция алгоритма Джонсона в систему "1С:Предприятие" открывает широкие возможности для оптимизации производственных процессов. Рассмотрим пример, когда производственный процесс состоит из двух последовательных этапов, таких как раскрой ДСП и обработка на станке для облицовки кромок. Каждая деталь должна пройти оба этапа обработки, и время обработки на каждом станке зависит от типа детали и используемых материалов. В системе "1С:Предприятие" создается специализированная обработка, которая принимает на вход данные о времени обработки каждой детали на обоих этапах и применяет алгоритм Джонсона для определения оптимальной последовательности обработки деталей. Это позволяет сократить время выполнения заказов на 15%, снизить затраты на оплату труда и повысить удовлетворенность клиентов за счет своевременного выполнения заказов. Другим примером может служить предприятие пищевой промышленности, занимающееся производством кондитерских изделий. Производственный процесс состоит из двух последовательных этапов: этапа подготовки сырья и этапа выпечки. На этапе подготовки сырья необходимо смешать различные ингредиенты в определенных пропорциях, а на этапе выпечки необходимо выпечь полученную смесь в специальных печах. Время выполнения каждого этапа зависит от типа изделия и используемого оборудования.
В системе 1С:Предприятие создается специализированный модуль, который интегрируется с модулем управления производством. Модуль принимает на вход данные о времени выполнения каждого этапа для каждого типа изделия. На основании этих данных модуль реализует алгоритм Джонсона и выдает на выход оптимальный план производства, минимизирующий общее время выполнения всех заказов. Полученный план используется для планирования работы производственных линий и для контроля за выполнением заказов. В результате внедрения алгоритма Джонсона предприятие смогло увеличить объем производства на 10%, снизить затраты на электроэнергию и повысить срок годности продукции за счет более равномерного распределения нагрузки на оборудование.
Еще одним примером является логистическая компания, занимающаяся доставкой грузов. Процесс доставки состоит из двух последовательных этапов: этапа приема груза на складе и этапа отгрузки груза клиенту. Время выполнения каждого этапа зависит от типа груза, объема и расстояния до клиента. В системе 1С:Предприятие создается специализированная подсистема, которая интегрируется с модулем управления транспортом. Подсистема принимает на вход данные о времени выполнения каждого этапа для каждого груза. На основании этих данных подсистема реализует алгоритм Джонсона и выдает на выход оптимальный план доставки грузов, минимизирующий общее время выполнения всех заказов.
Полученный план используется для планирования маршрутов транспортных средств и для контроля за выполнением заказов. В результате внедрения алгоритма Джонсона логистическая компания смогла сократить время доставки грузов на 20%, снизить затраты на топливо и повысить удовлетворенность клиентов за счет более быстрой и надежной доставки. Эти примеры демонстрируют, что алгоритм Джонсона может быть успешно применен в различных отраслях промышленности для оптимизации производственных и логистических процессов. Интеграция алгоритма в систему 1С:Предприятие позволяет предприятиям автоматизировать процесс планирования и управления, повысить эффективность использования ресурсов и улучшить свои конкурентные позиции на рынке.
Алгоритм Джонсона: Актуальность в 1С:Предприятии.
Актуальность алгоритма Джонсона в 1С:Предприятии обусловлена несколькими факторами. Во-первых, существует множество предприятий, где производственные процессы состоят из двух последовательных этапов, соответствующих условиям применения алгоритма. Например, можно разработать гибридный алгоритм, который будет использовать алгоритм Джонсона для оптимизации последовательности выполнения задач на двух ключевых станках, а для остальных станков применять другие, более простые методы.
В-третьих, алгоритм Джонсона может использоваться в качестве учебного при его применении. В частности, он не подходит для задач с более чем двумя станками, для задач с переменным порядком обработки задач на станках, а также для задач с другими факторами, такими как приоритеты задач, сроки выполнения и доступность ресурсов.
В таких случаях следует использовать другие, более сложные методы оптимизации, такие как генетические алгоритмы, имитация отжига и метод ветвей и границ. При выборе оптимального метода необходимо учитывать конкретные условия задачи, требования к точности решения и доступные вычислительные ресурсы. Также важно помнить, что алгоритм Джонсона, как и любой другой метод оптимизации, не снизить издержки и улучшить свои конкурентные позиции на рынке. В заключение, стоит отметить, что алгоритм Джонсона является важным элементом теории расписаний и может быть успешно применен для решения определенных задач в 1С:Предприятии. Однако, для достижения максимальной эффективности необходимо учитывать его ограничения и комплексно подходить к управлению производственными процессами.
Представьте, что у вас есть несколько заказов, которые нужно выполнить на двух станках. Каждый заказ требует определённого времени на каждом станке. Ваша задача — найти такую последовательность выполнения заказов, чтобы общее время, затраченное на выполнение всех заказов, было минимальным.
Функция АлгоритмДжонсона(Заказы)
// Создаем массивы для групп заказов
Массив1 = Новый Массив; // Заказы, где время на первом станке меньше или равно времени на втором станке
Массив2 = Новый Массив; // Заказы, где время на первом станке больше времени на втором станке
// Распределяем заказы по группам
Для Индекс = 0 По Заказы.Количество() - 1 Цикл
Если Заказы[Индекс][0] <= Заказы[Индекс][1] Тогда
Массив1.Добавить(Новый Массив);
Массив1[Массив1.Количество() - 1].Добавить(Заказы[Индекс][0]); // Время на первом станке
Массив1[Массив1.Количество() - 1].Добавить(Индекс); // Индекс заказа
Иначе
Массив2.Добавить(Новый Массив);
Массив2[Массив2.Количество() - 1].Добавить(Заказы[Индекс][1]); // Время на втором станке
Массив2[Массив2.Количество() - 1].Добавить(Индекс); // Индекс заказа
КонецЕсли;
КонецЦикла;
// Сортируем Массив1 по возрастанию времени на первом станке
Список1 = Новый СписокЗначений;
Для Каждого ЭлементМассива Из Массив1 Цикл
Список1.Добавить(ЭлементМассива, ЭлементМассива[0]); // Значение - массив, Значение - время на первом станке
КонецЦикла;
Список1.СортироватьПоЗначению(НаправлениеСортировки.Возр);
Массив1Отсортированный = Новый Массив;
Для Каждого ЭлементСписка Из Список1 Цикл
Массив1Отсортированный.Добавить(ЭлементСписка.Значение);
КонецЦикла;
// Сортируем Массив2 по убыванию времени на втором станке
Список2 = Новый СписокЗначений;
Для Каждого ЭлементМассива Из Массив2 Цикл
Список2.Добавить(ЭлементМассива, ЭлементМассива[0]); // Значение - массив, Значение - время на втором станке
КонецЦикла;
Список2.СортироватьПоЗначению(НаправлениеСортировки.Убыв);
Массив2Отсортированный = Новый Массив;
Для Каждого ЭлементСписка Из Список2 Цикл
Массив2Отсортированный.Добавить(ЭлементСписка.Значение);
КонецЦикла;
// Формируем оптимальную последовательность
ОптимальнаяПоследовательность = Новый Массив;
// Добавляем заказы из Массив1
Для Каждого ЭлементМассива Из Массив1Отсортированный Цикл
ОптимальнаяПоследовательность.Добавить(ЭлементМассива[1] + 1); // Индекс заказа (начинаем с 1)
КонецЦикла;
// Добавляем заказы из Массив2
Для Каждого ЭлементМассива Из Массив2Отсортированный Цикл
ОптимальнаяПоследовательность.Добавить(ЭлементМассива[1] + 1); // Индекс заказа (начинаем с 1)
КонецЦикла;
// Рассчитываем общее время выполнения
ОбщееВремя = 0;
ВремяСтанок1 = 0;
ВремяСтанок2 = 0;
Для Индекс = 0 По ОптимальнаяПоследовательность.Количество() - 1 Цикл
НомерЗаказа = ОптимальнаяПоследовательность[Индекс] - 1; // Получаем индекс заказа из массива Заказы (начинаем с 0)
ВремяСтанок1 = ВремяСтанок1 + Заказы[НомерЗаказа][0];
ВремяСтанок2 = Макс(ВремяСтанок1, ВремяСтанок2) + Заказы[НомерЗаказа][1];
КонецЦикла;
ОбщееВремя = ВремяСтанок2;
// Формируем строку с последовательностью заказов
СтрокаПоследовательности = "";
Для Индекс = 0 По ОптимальнаяПоследовательность.Количество() - 1 Цикл
СтрокаПоследовательности = СтрокаПоследовательности + ОптимальнаяПоследовательность[Индекс];
Если Индекс < ОптимальнаяПоследовательность.Количество() - 1 Тогда
СтрокаПоследовательности = СтрокаПоследовательности + " -> ";
КонецЕсли;
КонецЦикла;
Результат = Новый Структура;
Результат.Вставить("Последовательность", СтрокаПоследовательности);
Результат.Вставить("ОбщееВремя", ОбщееВремя);
Возврат Результат;
КонецФункции
Выведем начальные данные на форму для восприятия начальных данных:
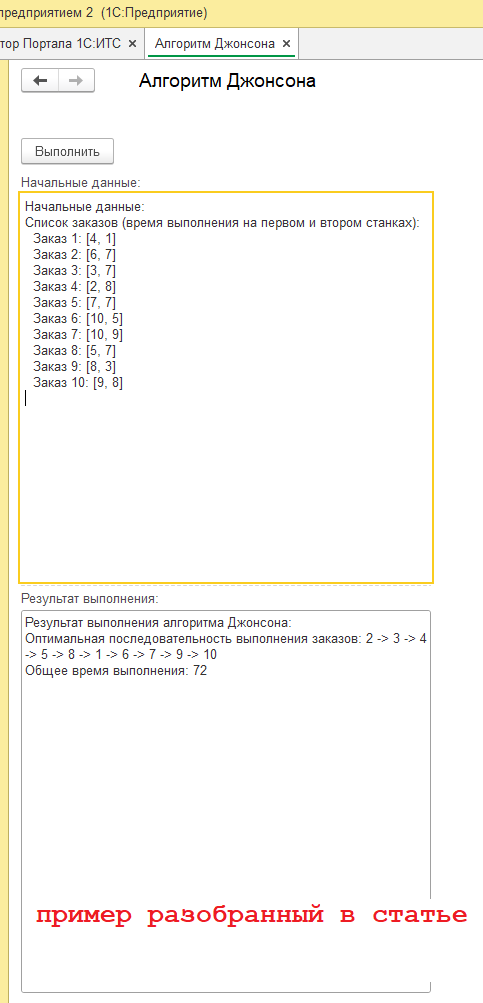
Начальные данные:
Список заказов (время выполнения на первом и втором станках):
Заказ 1: [4, 1]
Заказ 2: [6, 7]
Заказ 3: [3, 7]
Заказ 4: [2, 8]
Заказ 5: [7, 7]
Заказ 6: [10, 5]
Заказ 7: [10, 9]
Заказ 8: [5, 7]
Заказ 9: [8, 3]
Заказ 10: [9, 8]
В "Начальных данных" вы видите список заказов. Для каждого заказа указано два числа: первое — время выполнения на первом станке, второе — время выполнения на втором станке. Например, для "Заказа 1" время выполнения на первом станке равно 4, а на втором — 1.
В результате обработка выдает результат:
Результат выполнения алгоритма Джонсона:
Оптимальная последовательность выполнения заказов: 2 -> 3 -> 4 -> 5 -> 8 -> 1 -> 6 -> 7 -> 9 -> 10
Общее время выполнения: 72
"Результат выполнения алгоритма Джонсона" показывает, как лучше всего выполнить эти заказы, чтобы потратить меньше всего времени:
Оптимальная последовательность выполнения заказов: 2 -> 3 -> 4 -> 5 -> 8 -> 1 -> 6 -> 7 -> 9 -> 10 Это означает, что сначала нужно выполнить "Заказ 2", потом "Заказ 3", затем "Заказ 4" и так далее, до "Заказа 10".
Общее время выполнения: 72 Это общее время, которое потребуется, чтобы выполнить все заказы в указанной последовательности. Этот показатель минимален для данной задачи, при условии, что мы придерживаемся рассчитанной последовательности.
Представьте, что вы выполняете заказы в случайном порядке. В этом случае общее время выполнения может быть значительно больше, чем 72. Алгоритм Джонсона помогает вам избежать лишних затрат времени и повысить эффективность производства.
Что даёт оптимальная последовательность?
В данном конкретном примере, следуя предложенной последовательности (2 -> 3 -> 4 -> 5 -> 8 -> 1 -> 6 -> 7 -> 9 -> 10), вы завершите все работы за 72 единицы времени. Любая другая последовательность, скорее всего, потребует больше времени на выполнение всех заказов. Сокращение времени выполнения напрямую влияет на снижение издержек, увеличение пропускной способности производства и, в конечном итоге, на повышение прибыли предприятия.
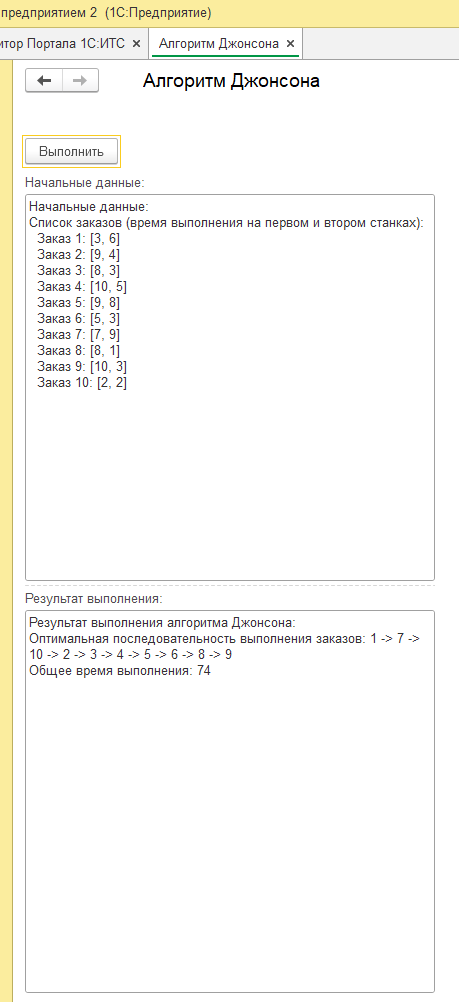
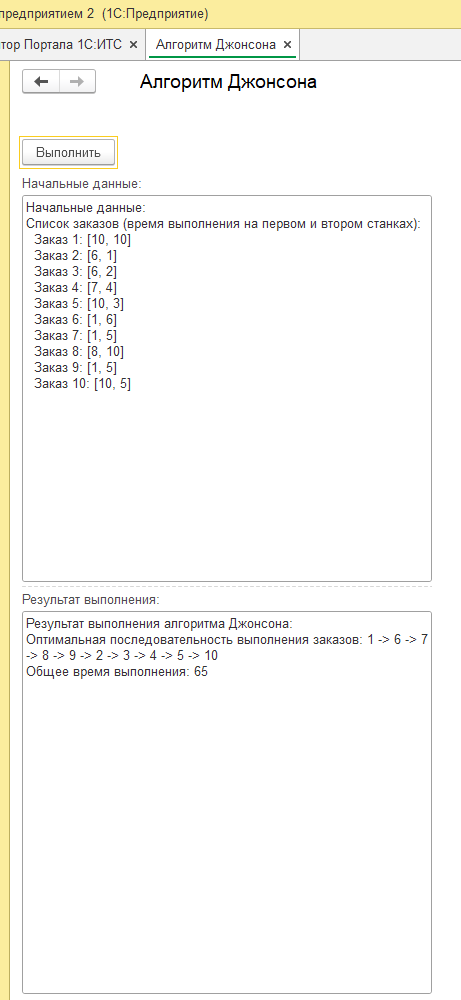
Статья для начинающих программистов. Код рабочей обработки прилагаю (массив с временем выполнения для заказов формирую в цикле через ГСЧ. Другие примеры см. скриншоты.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.13.82
Вступайте в нашу телеграмм-группу Инфостарт