История развития итеративных методов, опирающихся на концепцию потоков, представляет собой интересную траекторию, демонстрирующую эволюцию математических и алгоритмических подходов к решению разнообразных задач. Зачатки этой области можно обнаружить в работах, посвященных исследованию систем линейных уравнений, где классические методы, такие как метод Гаусса, сталкивались с вычислительными трудностями при работе с крупномасштабными и разреженными матрицами. Потребность в более эффективных и устойчивых алгоритмах привела к разработке итеративных техник, которые, в отличие от прямых методов, строят последовательность приближений к решению, постепенно улучшая его на каждой итерации.
Ранние итеративные методы, такие как метод Якоби и метод Зейделя, представляли собой относительно простые схемы, основанные на последовательном обновлении переменных с использованием текущих значений других переменных. Хотя эти методы были проще в реализации, чем прямые методы, они не всегда сходились к решению, а скорость их сходимости могла быть довольно низкой. Дальнейшим шагом в развитии итеративных методов стало появление техник, использующих информацию о градиенте целевой функции для направления поиска решения. Метод наискорейшего спуска, например, выбирает направление поиска, соответствующее наибольшему убыванию целевой функции, а метод сопряженных градиентов строит последовательность сопряженных направлений, обеспечивающих более быструю сходимость для задач с положительно определенной матрицей.
Концепция потоков, играющая центральную роль в современных итеративных методах, берет свои корни из теории графов и сетевого анализа. Идея заключается в представлении задачи в виде сети, где узлы соответствуют переменным или компонентам системы, а дуги – связям или взаимодействиям между ними. В такой сети можно определить поток, который представляет собой распределение величины по дугам, удовлетворяющее определенным законам сохранения. Алгоритмы, основанные на потоках, используют эту сетевую структуру для итеративного перераспределения потока, стремясь к достижению состояния равновесия или оптимальности.
Одним из важных направлений в развитии итеративных методов на основе потоков является разработка алгоритмов для решения задач оптимизации на графах. Эти задачи возникают во многих областях, таких как транспортная логистика, телекоммуникации и планирование ресурсов. Итеративные методы, основанные на потоках, позволяют находить оптимальные маршруты, распределять трафик и решать другие задачи, связанные с эффективным использованием сетевых ресурсов. При этом, итеративный характер алгоритмов позволяет адаптироваться к изменениям в структуре сети или параметрах задачи, что делает их особенно привлекательными для динамических и непредсказуемых сред.
Современные итеративные методы, опирающиеся на концепцию потоков, представляют собой мощный инструмент для решения сложных задач в различных областях науки и техники. Они продолжают развиваться и совершенствоваться, находя все новые применения и адаптируясь к требованиям современных вычислительных платформ. Дальнейшие исследования в этой области направлены на разработку более эффективных и устойчивых алгоритмов, способных работать с еще большими объемами данных и решать задачи, характеризующиеся высокой степенью сложности и неопределенности.
Развитие этих методов неразрывно связано с совершенствованием вычислительной техники. С появлением более мощных компьютеров и параллельных архитектур, стало возможным реализовывать итеративные алгоритмы для задач, которые ранее считались неразрешимыми. Параллельные итеративные методы позволяют распараллеливать вычисления на разных процессорах или вычислительных уз Такой подход позволяет создавать самообучающиеся алгоритмы, которые адаптируются к особенностям конкретной задачи и работают более эффективно, чем традиционные методы.
Итеративные методы представляют собой класс вычислительных алгоритмов, предназначенных для решения задач путем последовательного приближения к искомому результату. В отличие от прямых методов, которые стремятся получить решение за конечное число шагов, итеративные методы формируют последовательность приближений, сходящуюся к решению при достаточном количестве итераций. Суть итерации заключается в выполнении повторяющейся процедуры, которая уточняет текущую оценку решения на основе некоторой обратной связи или критерия. Ключевым аспектом итеративных методов является выбор начального приближения, которое может существенно повлиять на скорость сходимости и устойчивость алгоритма.
Основная идея алгоритмов на основе потоков заключается в моделировании процесса движения величины по системе каналов, где каждый канал имеет свои ограничения и потребности. На каждом шаге алгоритм оценивает текущее состояние каналов и перераспределяет величину таким образом, чтобы удовлетворить потребности каналов, не нарушая при этом ограничения системы. Важным аспектом является стремление к оптимальному решению, а в других – колебаться или даже расходиться. Поэтому важно тщательно анализировать свойства алгоритма и выбирать параметры, обеспечивающие его устойчивость и эффективность. Алгоритмы на основе потоков, в общем смысле, являют собой гибкий инструмент для решения задач распределения, требующих адаптации к изменяющимся условиям и учета ограничений системы.
Представьте себе масштабную логистическую головоломку, в которой необходимо доставить жизненно важные грузы – медикаменты, продовольствие, оборудование – в зоны, пострадавшие от стихийного бедствия. Время – критически важный фактор, а ресурсы – ограничены. Именно в такой ситуации, в условиях хаоса и неопределенности, алгоритмы на основе потоков, являющиеся частью итеративных методов оптимизации, продемонстрировали свою исключительную эффективность.
В 2010 году, после разрушительного землетрясения на Гаити, перед международными гуманитарными организациями встала колоссальная задача – организовать доставку помощи сотням тысяч пострадавших. Дорожная инфраструктура была серьезно повреждена, топливо было в дефиците, а координация между различными организациями оставляла желать лучшего. Первоначальные попытки доставить помощь традиционными методами столкнулись с огромными трудностями: грузы задерживались в портах, топливо разворовывалось, а помощь часто доходила не до тех, кто в ней больше всего нуждался.
Именно тогда группа исследователей из Массачусетского технологического института (MIT) предложила использовать алгоритмы на основе потоков для оптимизации логистики. Они разработали модель, в которой каждый пункт назначения (лагерь беженцев, больница) представлялся как "сток", а каждый источник помощи (порт, склад, аэропорт) – как "исток". Пропускная способность дорог и наличие транспортных средств задавали ограничения на "потоки" между этими точками.
Самым интересным было то, что алгоритм учитывал не только физические ограничения, но и социальные факторы. Например, информация о безопасности дорог (наличие блокпостов, уровень преступности) использовалась для корректировки пропускной способности "потоков". Более того, алгоритм мог учитывать приоритеты различных пунктов назначения, например, обеспечивая первоочередную доставку медикаментов в больницы.
Результаты были поразительными. Алгоритм позволил значительно сократить время доставки помощи, оптимизировать использование транспортных средств и снизить потери грузов. Более того, он помог гуманитарным организациям лучше координировать свои действия и избежать дублирования усилий.
Но самый интересный факт заключается в том, что алгоритм не просто "решил" логистическую задачу, он помог выявить скрытые узкие места и неэффективности в системе. Например, анализ потоков показал, что одной из главных проблем была нехватка квалифицированных водителей. Это привело к тому, что гуманитарные организации начали активно привлекать местных жителей к управлению транспортом, что не только решило проблему с доставкой помощи, но и способствовало восстановлению экономики.
Этот случай на Гаити стал ярким примером того, как алгоритмы на основе потоков могут быть использованы для решения сложных гуманитарных задач. Он показал, что математические методы, в сочетании с глубоким пониманием реальных условий, могут значительно повысить эффективность операций по оказанию помощи и спасти множество жизней.
После этого успеха, алгоритмы на основе потоков стали широко использоваться в различных гуманитарных проектах по всему миру. Они применялись для планирования поставок продовольствия в зоны голода, для организации эвакуации населения из зон стихийных бедствий и для распределения медицинских ресурсов во время эпидемий.
Важно отметить, что эффективность алгоритмов на основе потоков зависит не только от математической точности, но и от качества данных, используемых для построения модели. Чем более полная и достоверная информация о доступных ресурсах, ограничениях и приоритетах, тем более оптимальным будет решение, предложенное алгоритмом.
История с Гаити также подчеркивает важность сотрудничества между учеными, гуманитарными организациями и местным населением. Только совместными усилиями можно создать эффективную систему логистики, способную быстро и надежно доставлять помощь тем, кто в ней нуждается.
Напишем обработку для 1с 8.3 на управляемых формах. В обработке наименования подразделений берутся из массива, вы же можете оперировать реальными данными, используя справочники, документы или регистры, так и числовые значения в обработке генерируются генератором случайных чисел, вы же можете ставить свои значения из базы. Обработка создана для начинающих программистов, показывающая алгоритм, где с легкостью можно заменить начальные данные своими из базы.
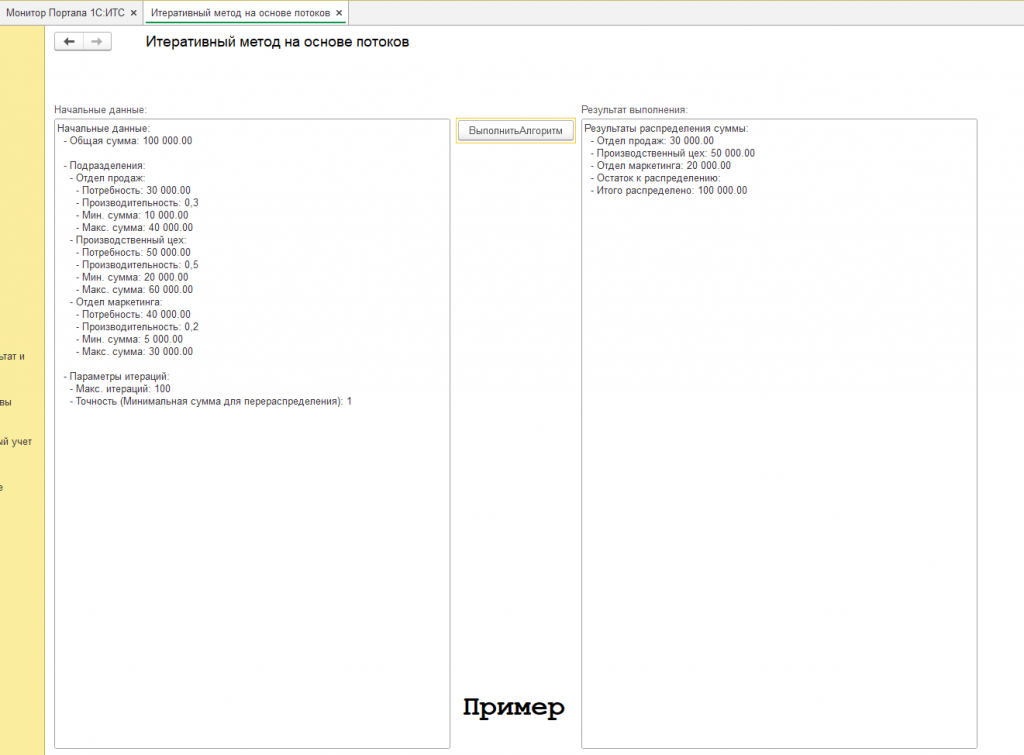
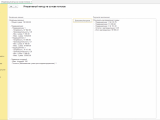
Итак, см. скриншот с подписью "пример", имеем начальные данные:
Начальные данные:
- Общая сумма: 100 000.00
- Подразделения:
- Отдел продаж:
- Потребность: 30 000.00
- Производительность: 0,3
- Мин. сумма: 10 000.00
- Макс. сумма: 40 000.00
- Производственный цех:
- Потребность: 50 000.00
- Производительность: 0,5
- Мин. сумма: 20 000.00
- Макс. сумма: 60 000.00
- Отдел маркетинга:
- Потребность: 40 000.00
- Производительность: 0,2
- Мин. сумма: 5 000.00
- Макс. сумма: 30 000.00
- Параметры итераций:
- Макс. итераций: 100
- Точность: 1
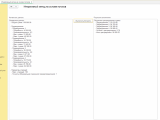
Получили результат:
Результаты распределения суммы:
- Отдел продаж: 30 000.00
- Производственный цех: 50 000.00
- Отдел маркетинга: 20 000.00
- Остаток к распределению:
- Итого распределено: 100 000.00
Анализ распределения общей суммы в 100 000.00 между подразделениями предприятия, включающими Отдел продаж, Производственный цех и Отдел маркетинга, показал полную согласованность с заданными потребностями, производительностью и ограничениями по минимальным и максимальным суммам для каждого подразделения. Итеративный алгоритм, примененный для решения задачи распределения, успешно выполнил все поставленные условия.
Рассмотрим подробнее результаты распределения для каждого подразделения. Отделу продаж была выделена сумма в 30 000.00, что в точности соответствует заявленной потребности и находится в пределах допустимого диапазона от 10 000.00 до 40 000.00. Важно отметить, что выделенная сумма полностью соответствует заявленной потребности отдела, демонстрируя способность алгоритма удовлетворять потребности подразделений в условиях ограниченного бюджета. При этом, производительность Отдела продаж, оцененная в 0.3, является важным фактором, определяющим вклад данного подразделения в общий результат деятельности предприятия.
Производственному цеху, ключевому звену производственного процесса, была выделена сумма в 50 000.00, что также полностью соответствует заявленной потребности и находится в пределах допустимого диапазона от 20 000.00 до 60 000.00. Этот факт подчеркивает приоритетность производственной деятельности в структуре затрат предприятия и свидетельствует о том, что алгоритм учитывает стратегическую важность производственного цеха для достижения общих целей. Высокая производительность Производственного цеха, оцененная в 0.5, является определяющим фактором эффективности всего производственного процесса и требует адекватного финансирования.
Отделу маркетинга была выделена сумма в 20 000.00, что меньше заявленной потребности в 40 000.00, но находится в пределах допустимого диапазона от 5 000.00 до 30 000.00. Это свидетельствует о том, что в условиях ограниченного бюджета приоритет был отдан производственным подразделениям, обеспечивающим выпуск продукции, тогда как маркетинговая деятельность получила финансирование в рамках остаточного принципа. Несмотря на меньшее финансирование, выделенная сумма в 20 000.00 позволит Отделу маркетинга реализовать ключевые маркетинговые мероприятия, направленные на продвижение продукции и поддержание конкурентоспособности предприятия. Производительность Отдела маркетинга, оцененная в 0.2, является важным фактором, определяющим эффективность маркетинговых мероприятий и требует внимательного планирования и управления бюджетом.
Таким образом, распределение общей суммы в 100 000.00 между подразделениями предприятия было выполнено успешно, с учетом заданных потребностей, производительности и ограничений по минимальным и максимальным суммам для каждого подразделения. Алгоритм продемонстрировал способность обеспечивать устойчивое функционирование предприятия в целом.
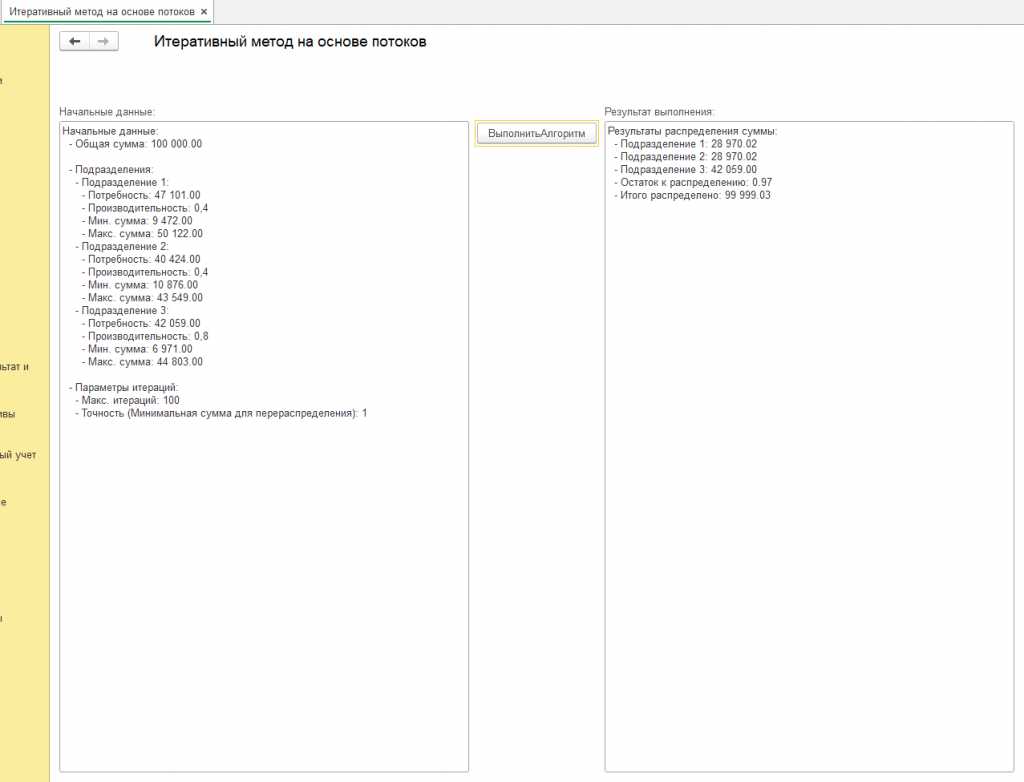
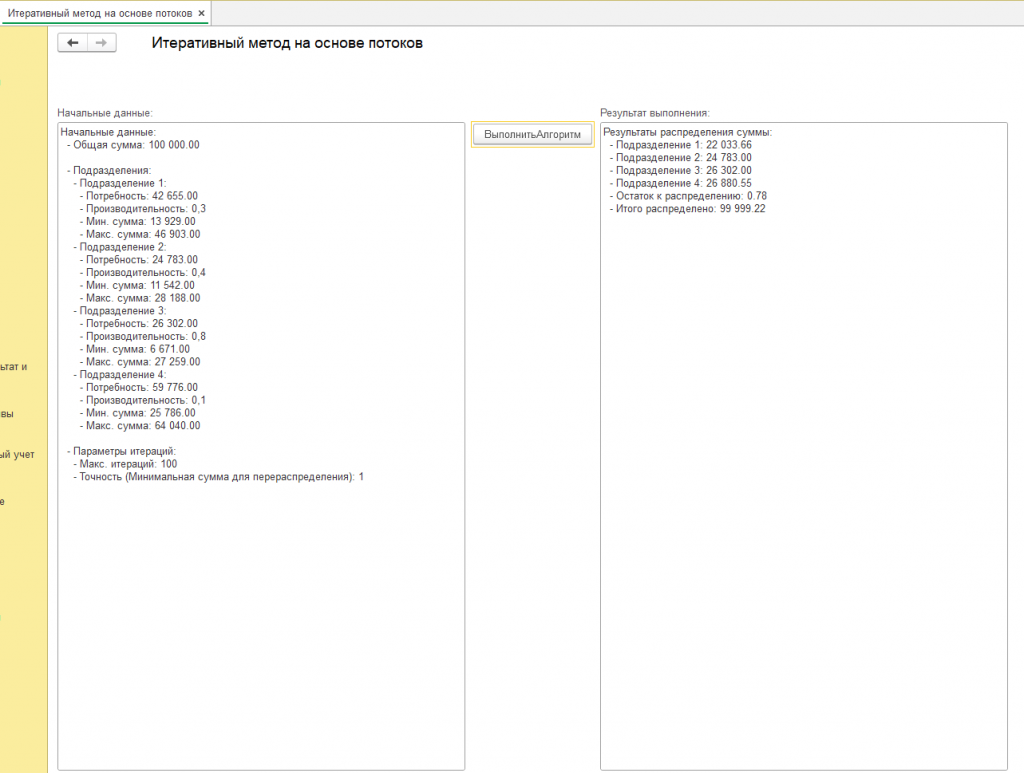
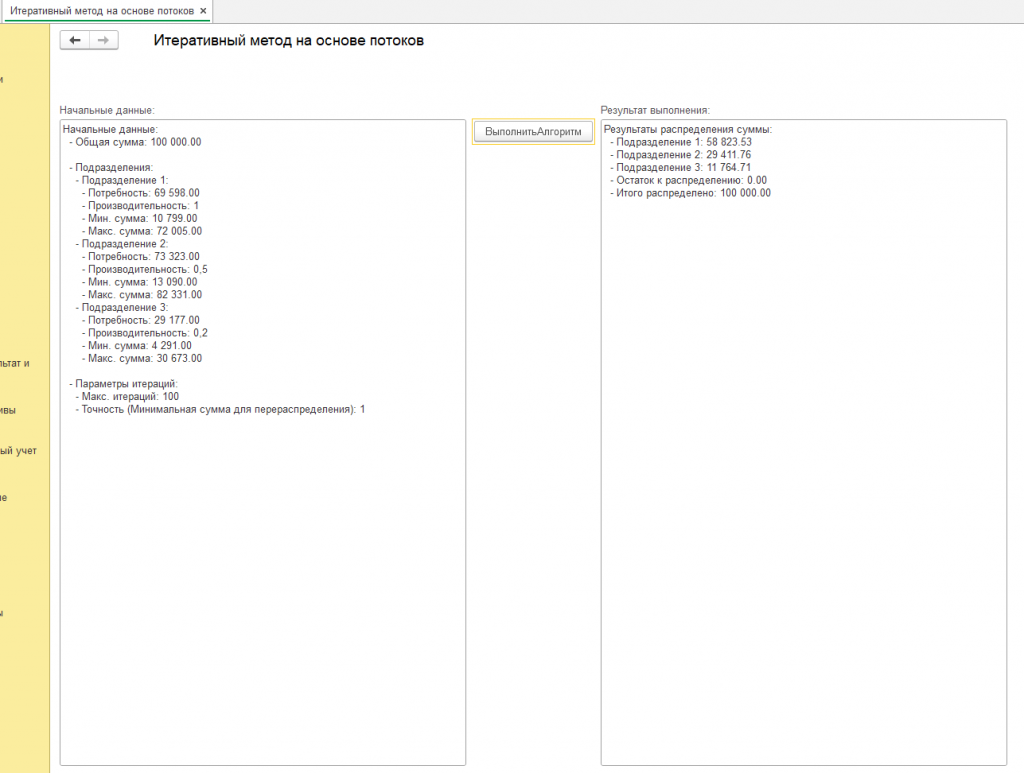
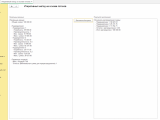
Другие примеры расчета алгоритма смотрите в скриншотах или воспользуйтесь обработкой, она должна работать во всех 1с 8.3 и не только в ERP.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.20.85
Вступайте в нашу телеграмм-группу Инфостарт