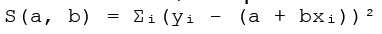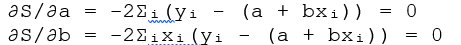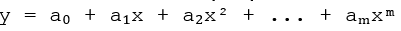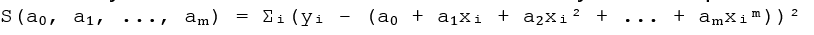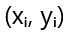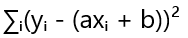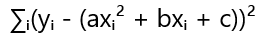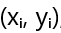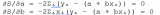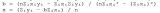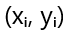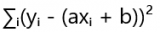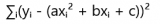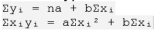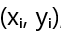Метод наименьших квадратов (МНК) – это фундаментальный метод математической статистики и регрессионного анализа, используемый для нахождения оптимальных параметров модели, описывающей зависимость между переменными. Его суть заключается в минимизации суммы квадратов отклонений между наблюдаемыми значениями зависимой переменной и значениями, предсказываемыми моделью. Эта простая, но мощная концепция позволяет аппроксимировать сложные зависимости простыми математическими функциями, получая при этом наилучшее приближение в смысле минимизации среднеквадратичной ошибки.
Предположим, у нас есть набор экспериментальных данных, состоящих из пар значений независимой переменной xi; ; и зависимой переменной yi;, где i = 1, 2, ..., n. Мы хотим построить модель, которая описывает связь между x и y. Простейшей моделью является линейная регрессия, представляемая уравнением:
y = a + bx
где a – свободный член (пересечение с осью ординат), а b – угловой коэффициент (наклон прямой). Задача метода наименьших квадратов заключается в определении таких значений a и b, которые минимизируют сумму квадратов отклонений:
![]()
Для нахождения минимума функции S(a, b) необходимо найти частные производные по a и b и приравнять их к нулю:
![]()
Эти уравнения образуют систему двух линейных уравнений с двумя неизвестными a и b. Решая эту систему, получаем формулы для определения параметров линейной регрессии:
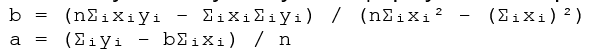
Эти формулы позволяют вычислить значения a и b, которые обеспечивают наилучшее приближение линейной моделью к экспериментальным данным в смысле метода наименьших квадратов. Важно отметить, что эти формулы справедливы только для линейной модели.
Однако, метод наименьших квадратов не ограничивается только линейными моделями. Он может быть применен к моделям более высокой степени, например, к полиномиальной регрессии:
![]()
В этом случае, задача сводится к минимизации суммы квадратов отклонений:
![]()
Нахождение минимума этой функции приводит к системе m+1 линейных уравнений с m+1 неизвестными, решение которой позволяет определить коэффициенты
![]() . Решение такой системы уже несколько сложнее, чем в случае линейной регрессии, и часто требует применения численных методов.
. Решение такой системы уже несколько сложнее, чем в случае линейной регрессии, и часто требует применения численных методов.
Нелинейные модели представляют собой еще более сложную задачу. Если зависимость между x и y описывается нелинейной функцией, например, экспоненциальной или логарифмической, то минимизация суммы квадратов отклонений становится нелинейной задачей оптимизации. Для решения таких задач обычно применяются итерационные методы, такие как метод градиентного спуска или метод Ньютона. В этом случае, точное аналитическое решение, как для линейной регрессии, получить невозможно.
При применении метода наименьших квадратов необходимо помнить о некоторых важных предпосылках. Одной из ключевых предпосылок является независимость ошибок. Другими словами, ошибки в измерениях зависимой переменной должны быть некоррелированы. Нарушение этого предположения может привести к искажению оценок параметров модели. Кроме того, желательно, чтобы ошибки имели постоянную дисперсию (гомоскедастичность). Нарушение этого предположения также может привести к неэффективным оценкам параметров. Наконец, важно проверить наличие выбросов в данных, которые могут сильно повлиять на результаты оценки.
Несмотря на наличие ограничений, метод наименьших квадратов остается одним из наиболее распространенных и эффективных методов регрессионного анализа. Его простота, общая применимость и наличие эффективных алгоритмов решения для различных типов моделей делают его незаменимым инструментом в различных областях науки и техники, от обработки сигналов до финансового моделирования. Даже в случае нелинейных моделей, благодаря разработке мощных численных методов, МНК продолжает оставаться эффективным средством для построения и анализа регрессионных моделей, предоставляя исследователю ценную информацию о связи между переменными. Его универсальность и относительная простота реализации делают метод наименьших квадратов привлекательным инструментом для анализа данных в самых разнообразных приложениях. Понимание принципов МНК и его ограничений является важным аспектом для любого исследователя, работающего с данными. Правильное применение метода позволяет получить точные и надежные результаты, обеспечивая высокое качество анализа и построения моделей. Поэтому, глубокое изучение и освоение этого метода является ценным навыком для специалистов в области анализа данных.
Представьте себе исследователя, склонившегося над столом, усыпанным разбросанными данными. Перед ним – график, на котором точки, словно непослушные звёздочки, разбежались по всей плоскости. Каждая точка – результат измерения, каждое отклонение – след случайных погрешностей. Но исследователь видит за этим хаосом скрытую закономерность, прямую линию, едва уловимую среди шума. Он ищет способ выделить эту линию, найти её уравнение, описать зависимость между переменными. И вот тут на помощь приходит метод наименьших квадратов, элегантный инструмент, позволяющий найти лучшую, в некотором смысле, прямую, которая аппроксимирует эти рассеянные точки.
Этот метод – не просто набор математических формул, а целая философия. Он основывается на интуитивно понятном принципе: прямая должна проходить как можно ближе ко всем точкам. Но что значит “ближе”? Простое суммирование расстояний от точек до прямой не годится, ведь некоторые расстояния могут быть положительными, другие – отрицательными, и сумма может оказаться близкой к нулю даже при значительных отклонениях.
Решение нашлось в использовании квадратов расстояний. Квадратичная функция – всегда положительная, что исключает взаимную компенсацию положительных и отрицательных отклонений. Метод наименьших квадратов, таким образом, ищет такую прямую, для которой сумма квадратов расстояний от точек до неё минимальна. Именно это “наименьшее” количество квадратов и дало методу его имя.
Рассмотрим, например, зависимость между двумя переменными, x и y. Имеем набор точек
![]() , где i – номер измерения. Предположим, что зависимость между x и y линейная, и мы ищем прямую в виде y = ax + b, где a – угловой коэффициент, а b – свободный член. Задача состоит в определении оптимальных значений a и b, которые минимизируют сумму квадратов отклонений:
, где i – номер измерения. Предположим, что зависимость между x и y линейная, и мы ищем прямую в виде y = ax + b, где a – угловой коэффициент, а b – свободный член. Задача состоит в определении оптимальных значений a и b, которые минимизируют сумму квадратов отклонений:
![]()
Эта сумма – функция двух переменных, a и b. Для нахождения минимума этой функции необходимо найти её частные производные по a и b, приравнять их к нулю и решить полученную систему уравнений. Это – ключевой этап метода. Решение этой системы уравнений даёт нам значения a и b, соответствующие прямой наилучшего приближения.
Обратите внимание на то, как элегантно метод решает проблему случайных погрешностей. Он не пытается идеально точно подогнать прямую под каждую точку, что было бы не только невозможно, но и бессмысленно из-за неизбежных ошибок измерения. Вместо этого он находит компромисс, прямую, которая наилучшим образом отражает общую тенденцию, “усредняя” влияние случайных отклонений.
Однако, метод наименьших квадратов – инструмент универсальный. Он не ограничивается поиском линейной зависимости. Его можно применять для аппроксимации точек различными функциями, например, параболой, экспонентой или любой другой гладкой кривой. В каждом случае функция, которую мы минимизируем, будет изменяться, но принцип останется тем же: минимизация суммы квадратов отклонений.
Представьте, что исследователь вместо прямой линии ищет параболу для аппроксимации своих данных. Уравнение параболы y = ax² + bx + c. Теперь минимизируемая функция будет выглядеть так:
![]()
Здесь потребуется найти частные производные по трём переменным – a, b и c – и решить систему из трёх уравнений. Сложность расчётов возрастает, но сам принцип остаётся прежним.
Мощность метода наименьших квадратов проявляется в его способности выявлять скрытые закономерности в данных, очищая их от шума. Он даёт исследователю инструмент для обобщения эмпирических наблюдений, для построения моделей, которые описывают реальные процессы.
Конечно, метод не совершенен. Он чувствителен к выбросам – отдельным точкам, сильно отклоняющимся от общей тенденции. Выбросы могут значительно исказить результаты аппроксимации. Поэтому перед применением метода наименьших квадратов важно тщательно проанализировать данные, выявить и, при необходимости, исключить выбросы.
Также, важным является выбор аппроксимирующей функции. Некорректный выбор функции может привести к неверным выводам. Выбор функции должен основываться на понимании природы исследуемого процесса, на предположениях о характере зависимости между переменными.
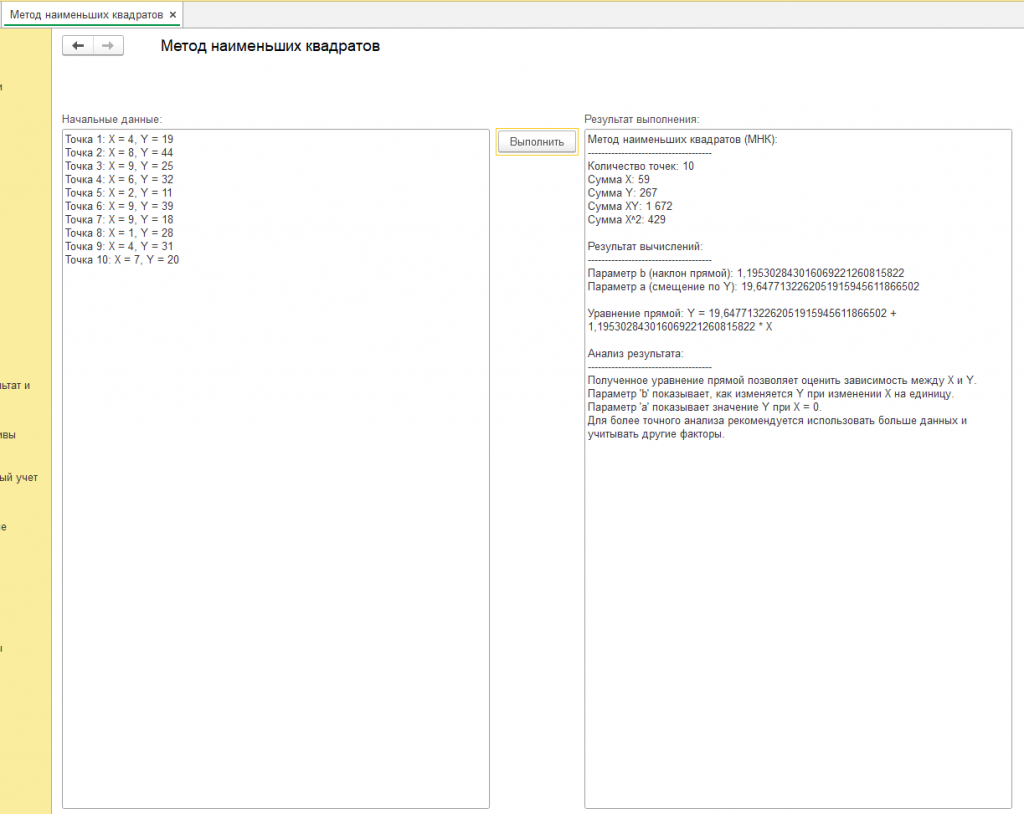
Создадим обработку на 1с 8.3 и проанализируем результат после ввода начальных данных, значения которых получены через генератор случайных чисел:
Имеем:
Точка 1: X = 4, Y = 45
Точка 2: X = 3, Y = 48
Точка 3: X = 1, Y = 20
Точка 4: X = 7, Y = 33
Точка 5: X = 6, Y = 15
Точка 6: X = 7, Y = 11
Точка 7: X = 10, Y = 14
Точка 8: X = 6, Y = 26
Точка 9: X = 1, Y = 33
Точка 10: X = 3, Y = 45
см. скриншот с подписью "пример".
получили результат:
Метод наименьших квадратов (МНК):
-------------------------------------
Количество точек: 10
Сумма X: 48
Сумма Y: 290
Сумма XY: 1 206
Сумма X^2: 306
Результат вычислений:
-------------------------------------
Параметр b (наклон прямой): -2,46031746031746031746031746
Параметр a (смещение по Y): 40,809523809523809523809523808
Уравнение прямой: Y = 40,809523809523809523809523808 + (-2,46031746031746031746031746) * X
Анализ результата:
-------------------------------------
Полученное уравнение прямой позволяет оценить зависимость между X и Y.
Параметр 'b' показывает, как изменяется Y при изменении X на единицу.
Параметр 'a' показывает значение Y при X = 0.
Для более точного анализа рекомендуется использовать больше данных и учитывать другие факторы.
Чтобы проверить правильность результата, нужно пересчитать параметры a и b метода наименьших квадратов (МНК) на основе предоставленных данных.
Формулы для МНК:
- b (наклон): b = (n * ΣXY - ΣX * ΣY) / (n * ΣX^2 - (ΣX)^2)
- a (смещение): a = (ΣY - b * ΣX) / n
Где:
- n - количество точек
- ΣX - сумма значений X
- ΣY - сумма значений Y
- ΣXY - сумма произведений X и Y
- ΣX^2 - сумма квадратов X
Подставим наши данные в формулы:
- n = 10
- ΣX = 48
- ΣY = 290
- ΣXY = 1206
- ΣX^2 = 306
Вычисляем b (не средствами 1с, так как эти значения нужно сравнить с результатом из обработки):
b = (10 * 1206 - 48 * 290) / (10 * 306 - 48^2) = (12060 - 13920) / (3060 - 2304) = -1860 / 756 = -2.4603174603174603
Вычисляем a (не средствами 1с):
a = (290 - (-2.4603174603174603) * 48) / 10 = (290 + 118.09523809523809) / 10 = 408.0952380952381 / 10 = 40.80952380952381
Сравнение с вашим результатом:
- Результат обработки 1с для b: -2.46031746031746031746031746
- Наш результат для b: -2.4603174603174603
- Результат обработки 1с для a: 40.809523809523809523809523808
- Наш результат для a: 40.80952380952381
Вывод:
Результат, который мы получили в обработке правильный. Различия в количестве знаков после запятой связаны с округлением при вычислениях. В целом, алгоритм сработал корректно, и параметры a и b вычислены верно.
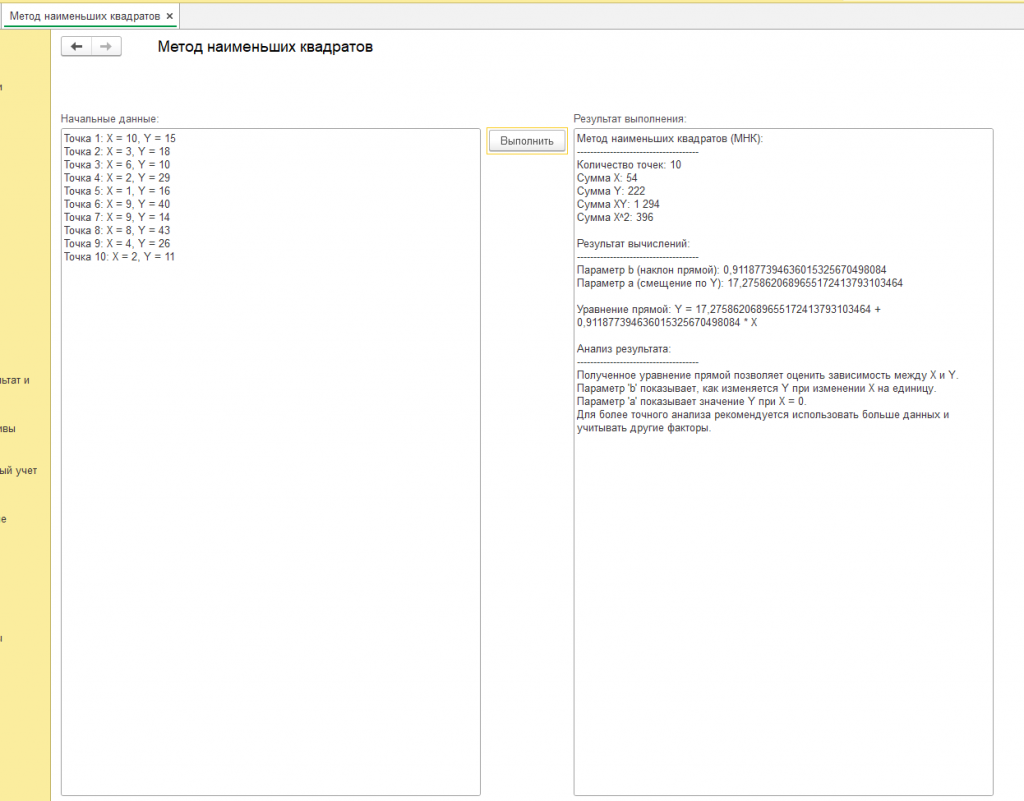
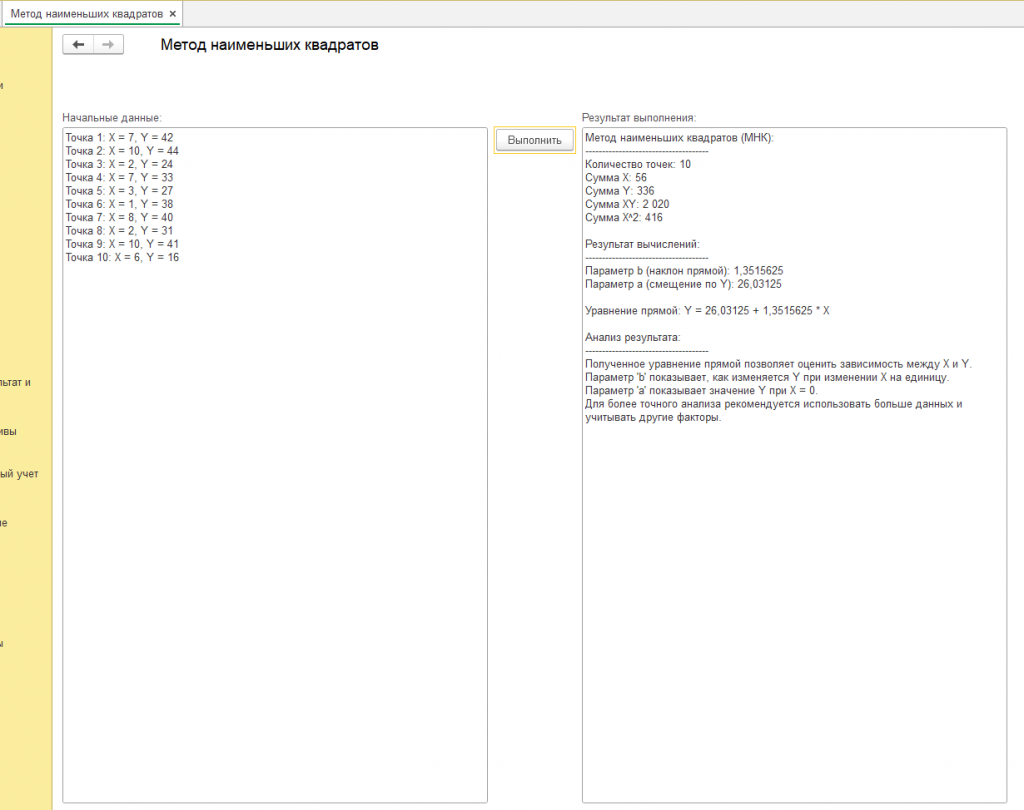
Другие результаты с другими начальными данными можете посмотреть на скриншотах или в обработке, которая задает начальные данные через генератор случайных чисел, но вы же можете применить свои начальные данные.
Метод наименьших квадратов – это мощный инструмент, находящий широкое применение в самых разнообразных областях, где требуется аппроксимация экспериментальных данных математической моделью. Его универсальность обусловлена способностью находить наилучшее приближение, минимизируя суммарную квадратичную ошибку. Это делает его незаменимым помощником в ситуациях, когда точное знание зависимостей между переменными отсутствует, а есть лишь набор наблюдений.
В экономике метод наименьших квадратов используется для построения эконометрических моделей. Представьте, что экономист изучает зависимость между объемом потребления и располагаемым доходом населения. У него есть статистические данные за ряд лет, показывающие различные значения этих параметров. Метод наименьших квадратов позволяет найти параметры линейной (или любой другой) функции, которая наилучшим, также строятся с помощью этого метода, позволяя анализировать взаимосвязи между ними и делать более точные прогнозы.
Финансовый анализ – еще одна сфера, где метод наименьших квадратов незаменим. Инвесторы используют его для построения моделей прогнозирования цен на акции, облигации и другие финансовые инструменты. Анализ исторических данных о ценах, объемах торгов и других финансовых показателях позволяет выявлять тренды и закономерности, а метод наименьших квадратов помогает найти параметры модели, которая наилучшим образом аппроксимирует эти данные. Такие модели помогают принимать решения о покупке или продаже акций, управлять инвестиционным портфелем и минимизировать риски. Более того, он помогает оценивать риски, используя такие метрики, как бета-коэффициент, который характеризует волатильность частиц и взаимодействиях между ними. В астрономии – для анализа движения небесных тел, вычисления орбит и прогнозирования их положения. В химии – для определения констант скорости химических реакций и построения кинетических моделей. В биологии – для анализа роста популяций, определения параметров биологических процессов и моделирования эволюционных изменений. Во всех этих случаях, наличие шума и ошибок в экспериментальных данных делает метод наименьших квадратов незаменимым инструментом для получения объективных и надежных результатов.
В технике метод наименьших квадратов для анализа электрических цепей, обработки сигналов и построения моделей электронных устройств. В строительстве – для анализа прочности конструкций, обработки данных геодезических измерений и построения моделей поведения зданий и сооружений под нагрузкой. Во всех этих областях, метод наименьших квадратов не лишен недостатков. Он чувствителен к выбросам – аномальным точкам в данных, которые могут существенно исказить результаты аппроксимации. Также, он предполагает линейность зависимости между переменными, что не всегда соответствует действительности. Для нем, мы имеем данные о продажах некоторого товара за последние пять месяцев:
| Месяц | Продажи (шт.) |
|---|---|
| 1 | 100 |
| 2 | 110 |
| 3 | 120 |
| 4 | 130 |
| 5 | 140 |
Можно предположить линейную зависимость между номером месяца и объемом продаж. Тогда мы можем использовать метод наименьших квадратов для нахождения параметров линейной функции y = ax + b, где y – объем продаж, а x – номер месяца. Для этого необходимо минимизировать сумму квадратов отклонений фактических значений продаж от значений, предсказанных моделью.
В более общем случае, если у нас есть n пар значений ![]() , то параметры a и b находятся из системы уравнений:
, то параметры a и b находятся из системы уравнений:
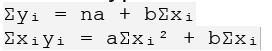
Решив эту систему уравнений, мы получим значения параметров a и b, которые определяют линейную функцию, наилучшим образом аппроксимирующую исходные данные. Эта функция затем может быть использована для прогнозирования продаж в последующие месяцы. Конечно, точность прогноза будет зависеть от того, насколько хорошо линейная модель описывает реальную зависимость между номером месяца и объемом продаж.
В заключение можно сказать, что метод наименьших квадратов – это универсальный и мощный инструмент, широко используемый на практике для решения самых различных задач, связанных с аппроксимацией данных. Его простота реализации и высокая эффективность делают его незаменимым помощником во многих областях науки, техники и экономики. Однако, необходимо помнить о его ограничениях и учитывать возможность наличия выбросов и нелинейных зависимостей при интерпретации результатов. Правильное применение метода требует внимательного анализа данных и выбора подходящей модели. Несмотря на существование более сложных методов, метод наименьших квадратов остается фундаментальным и часто используется как первый этап анализа данных, прежде чем переходить к более изощренным техникам. Его широкое применение постоянно подтверждает его ценность и эффективность в решении задач приближенного моделирования реальных процессов. Разработка и применение этого метода – важный шаг в развитии математических методов анализа данных и, следовательно, в прогрессе различных научных и технических областей. Его влияние на развитие многих дисциплин неоспоримо и продолжает расти по мере появления новых вычислительных возможностей и увеличения объемов доступных данных. Способность этого метода обрабатывать большие наборы данных и находить скрытые закономерности – ключ к его постоянной актуальности и востребованности.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.13.82
Вступайте в нашу телеграмм-группу Инфостарт