Алгоритм Гаусса, названный в честь выдающегося немецкого математика Карла Фридриха Гаусса, представляет собой систематический метод решения систем линейных уравнений. Основная идея заключается в последовательном исключении переменных для преобразования исходной системы к ступенчатому виду, что позволяет легко находить решения. Процесс начинается с выбора ведущего элемента в первом уравнении, который используется для исключения соответствующей переменной из последующих уравнений. Этот шаг повторяется для каждого следующего уравнения, постепенно формируя верхнетреугольную матрицу коэффициентов. После завершения прямого хода алгоритма выполняется обратная подстановка, начиная с последнего уравнения, чтобы определить значения всех переменных.
Важным аспектом алгоритма Гаусса является выбор ведущего элемента. В классической версии метода предполагается, что ведущий элемент не равен нулю, что может быть обеспечено перестановкой строк или столбцов матрицы. Однако на практике, особенно при работе с вычислительными системами, возникает необходимость в стратегиях частичного или полного выбора ведущего элемента для минимизации ошибок округления. Частичный выбор предполагает поиск максимального по модулю элемента в текущем столбце, тогда как полный выбор охватывает всю подматрицу, что повышает устойчивость алгоритма, но увеличивает вычислительную сложность.
Модификации алгоритма Гаусса нашли применение в различных областях, включая решение задач оптимизации, обработку сигналов и машинное обучение. Например, в методах наименьших квадратов, используемых для аппроксимации данных, алгоритм Гаусса-Жордана позволяет находить псевдообратные матрицы, что критически важно при работе с переопределенными или недоопределенными системами. Еще одной адаптацией является блочный метод Гаусса, который разбивает матрицу на подматрицы, что особенно эффективно при параллельных вычислениях и работе с большими массивами данных.
Сравнивая алгоритм Гаусса с другими методами, такими как метод Крамера или матричное обращение, можно отметить его вычислительную эффективность для систем средней размерности. Метод Крамера, основанный на вычислении определителей, становится непрактичным при большом числе переменных из-за экспоненциального роста сложности. Матричное обращение, хотя и элегантное теоретически, требует больше операций по сравнению с прямым применением алгоритма Гаусса. Однако для очень больших систем итерационные методы, такие как метод Якоби или метод сопряженных градиентов, могут оказаться более предпочтительными, особенно в условиях ограниченных вычислительных ресурсов.
Одним из ключевых преимуществ алгоритма Гаусса является его универсальность. Он применим к любым системам линейных уравнений, включая вырожденные случаи, когда система имеет бесконечно много решений или несовместна. В таких ситуациях алгоритм позволяет идентифицировать зависимости между уравнениями и определить базисные и свободные переменные. Однако при работе с плохо обусловленными системами, где малые изменения коэффициентов приводят к значительным отклонениям в решении, метод Гаусса без модификаций может давать неточные результаты. Это ограничение преодолевается за счет использования методов регуляризации или перехода к итерационным алгоритмам с контролем точности.
Современные вычислительные системы активно используют алгоритм Гаусса в сочетании с численными библиотеками, оптимизированными для конкретных архитектур. Библиотеки линейной алгебры, такие как LAPACK или BLAS, реализуют вариации метода с учетом особенностей процессоров и распределенных вычислений. В контексте машинного обучения алгоритм Гаусса применяется для решения задач регрессии, кластеризации и снижения размерности данных. Например, в методе главных компонент (PCA) сингулярное разложение матрицы, тесно связанное с алгоритмом Гаусса, позволяет выделять наиболее информативные признаки из многомерных наборов данных.
Развитие квантовых вычислений открывает новые перспективы для алгоритмов решения линейных систем. Квантовые версии метода Гаусса, такие как алгоритм Харроу-Хассидима-Ллойда, обещают экспоненциальное ускорение для определенных классов задач. Однако практическая реализация таких методов пока ограничена текущим уровнем развития квантовых технологий. Параллельно ведутся исследования в области гибридных алгоритмов, сочетающих классические и квантовые подходы, что может расширить область применения метода Гаусса в будущем.
В образовательном процессе алгоритм Гаусса остается фундаментальным инструментом для понимания основ линейной алгебры. Его изучение помогает развивать навыки работы с матрицами, системами уравнений и векторными пространствами. Многие учебные программы по математике и инженерии включают практические задания по реализации метода на различных языках программирования, что способствует глубокому усвоению материала. При этом акцент делается не только на механическом выполнении шагов алгоритма, но и на анализе его устойчивости, точности и вычислительной сложности.
Эволюция алгоритма Гаусса продолжается в направлении адаптации к новым вычислительным парадигмам. С появлением тензорных процессоров и специализированных ускорителей для задач искусственного интеллекта методы решения линейных систем требуют переосмысления с точки зрения параллелизма и эффективного использования памяти. Оптимизированные версии алгоритма, учитывающие иерархию кэшей и векторные инструкции, позволяют достигать высокой производительности даже на стандартных аппаратных платформах. Это делает алгоритм Гаусса не только исторически значимым, но и практически востребованным в эпоху больших данных и высокопроизводительных вычислений.
Метод Гаусса находит широкое применение в задачах, требующих решения систем линейных уравнений, что делает его незаменимым инструментом в инженерии, физике, экономике и компьютерных науках. Например, в электротехнике он используется для анализа цепей, где системы уравнений описывают токи и напряжения в узлах сети. В компьютерной графике алгоритм применяется для преобразований координат и работы с трехмерными объектами, а в экономике — для оптимизации ресурсов и моделирования сложных финансовых систем. Одной из ключевых адаптаций метода является модификация Гаусса-Жордана, которая расширяет его функциональность за счет одновременного приведения матрицы к диагональному виду, что упрощает нахождение обратной матрицы. Эта адаптация особенно полезна в криптографии и машинном обучении, где обратные матрицы используются для шифрования данных и решения задач регрессии.
Для повышения устойчивости метода в условиях ограниченной точности вычислений применяется стратегия выбора ведущего элемента. Этот подход минимизирует ошибки округления, переставляя строки матрицы так, чтобы на каждом шаге в качестве опорного выбирался максимальный по модулю элемент в столбце. Такая модификация критически важна при работе с плохо обусловленными системами, где даже незначительные погрешности могут привести к катастрофическим отклонениям в результатах. В вычислительной гидродинамике, например, подобные системы возникают при моделировании турбулентных потоков, и устойчивость алгоритма напрямую влияет на достоверность прогнозов.
Еще одной адаптацией метода Гаусса является блочная реализация, предназначенная для обработки больших матриц, которые не помещаются в оперативную память. Разделяя матрицу на блоки, алгоритм выполняет операции над частями данных, снижая нагрузку на кэш процессора и ускоряя вычисления. Это особенно актуально в задачах обработки сигналов и анализа больших данных, где размерность систем может достигать миллионов уравнений. В таких сценариях классический метод Гаусса становится непрактичным из-за кубической сложности, но блочные модификации позволяют эффективно распределять вычисления между узлами кластера.
Сравнивая метод Гаусса с альтернативными подходами, стоит отметить его преимущества перед методом Крамера, который, хотя и обладает теоретической элегантностью, становится неэффективным для систем с числом уравнений больше трех из-за экспоненциального роста вычислительных затрат. В отличие от него, метод Гаусса имеет полиномиальную сложность, что делает его применимым для задач средней размерности. Однако для очень больших и разреженных матриц итерационные методы, такие как метод Якоби или Гаусса-Зейделя, оказываются более предпочтительными. Эти алгоритмы не требуют полного хранения матрицы в памяти и могут быть остановлены при достижении заданной точности, что критично в задачах численного моделирования, где абсолютная точность часто менее важна, чем скорость сходимости.
Метод LU-разложения, тесно связанный с методом Гаусса, предлагает альтернативу для случаев, когда необходимо многократно решать системы с одной и той же матрицей коэффициентов, но разными правыми частями. Разложение матрицы на нижнюю и верхнюю треугольные позволяет сократить вычислительные затраты при повторных решениях, что востребовано, например, в задачах оптимизации с итеративным уточнением параметров. Однако сам процесс LU-разложения требует дополнительных операций по сравнению с классическим методом Гаусса, что делает его менее эффективным для однократного решения.
В контексте параллельных вычислений метод Гаусса сталкивается с ограничениями из-за последовательного характера операций исключения, тогда как методы на основе градиентного спуска или сопряженных направлений легче распараллеливаются. Тем не менее, гибридные подходы, сочетающие этап исключения Гаусса с итерационным уточнением, находят применение в высокопроизводительных вычислениях. Например, в квантовой химии такие гибриды используются для решения уравнений Хартри-Фока, где точность метода Гаусса дополняется скоростью итерационных схем.
Специализированные адаптации метода Гаусса продолжают развиваться для нишевых приложений. В робототехнике, например, модификации алгоритма учитывают структурные особенности матриц, возникающих при решении задач кинематики, что позволяет сократить время вычислений в реальном времени. В биоинформатике версии метода, оптимизированные для работы с разреженными данными, применяются для анализа геномных последовательностей, где системы уравнений отражают взаимосвязи между генами. Эти примеры иллюстрируют, как базовый алгоритм адаптируется под требования конкретных областей, сохраняя свою актуальность в условиях разнообразия вычислительных задач.
При сравнении с символическими методами, такими как те, что реализованы в системах компьютерной алгебры, метод Гаусса проигрывает в точности, но выигрывает в скорости для численных расчетов. Символьные подходы, способные работать с дробями и корнями, незаменимы в теоретических исследованиях, но их применение ограничено из-за высоких вычислительных затрат. В инженерных расчетах, где допустимы приближенные решения, метод Гаусса остается стандартом де-факто, особенно в сочетании с численными библиотеками, оптимизированными под конкретные архитектуры процессоров.
Выбор между методом Гаусса и альтернативными подходами зависит от специфики задачи: размерности системы, структуры матрицы коэффициентов, требований к точности и доступным вычислительным ресурсам. Гибридные стратегии, объединяющие сильные стороны разных методов, часто становятся оптимальным решением в современных приложениях, где универсальность уступает место специализированным оптимизациям.
Напишем для примера алгоритма Гауса решений линейных уравнений обработку на 1с 8.3, в которую все начальные числовые значения задаются генератором случайных чисел (можно заменить на свои реальные значения), и при каждом нажатии кнопки получаем для различных начальных данных верный результат.
Рассмотрим систему из трех уравнений с тремя неизвестными, которая часто возникает в задачах, связанных с расчетами в технике, экономике или логистике. Исходные уравнения выглядят так: ( см. скриншот с подписью "пример"):
Исходная система уравнений:
4x + 1y + 2z = 14
4x + 3y + 3z = 15
1x + 1y + 1z = 7
- Первое уравнение: 4x + y + 2z = 14.
- Второе уравнение: 4x + 3y + 3z = 15.
- Третье уравнение: x + y + z = 7.
Для решения этой системы применяется метод Гаусса — классический алгоритм, позволяющий последовательно упрощать уравнения, чтобы найти значения переменных. На первом шаге первое уравнение делится на коэффициент при x (4), чтобы упростить вычисления. В результате получается уравнение: x + 0,25y + 0,5z = 3,5. Далее из второго и третьего уравнений вычитается первое уравнение, умноженное на соответствующие коэффициенты, чтобы исключить x из этих строк. После преобразований второе уравнение принимает вид x + 2y + z = 1, а третье — x + 0,75y + 0,5z = 3,5.
Вывод результата нашей обработки:
Процесс решения методом Гаусса:
----------------------------------------
1. Нормализация первой строки:
Делим первую строку на 4:
1x + 0,25y + 0,5z = 3,5
2. Обнуление первого столбца во второй строке:
Вычитаем из второй строки первую, умноженную на 4:
x + 2y + 1z = 1
3. Обнуление первого столбца в третьей строке:
Вычитаем из третьей строки первую, умноженную на 1:
x + 0,75y + 0,5z = 3,5
4. Нормализация второй строки:
Делим вторую строку на 2:
x + 1y + 0,5z = 0,5
5. Обнуление второго столбца в третьей строке:
Вычитаем из третьей строки вторую, умноженную на 0,75:
x + y + 0,125z = 3,125
6. Нормализация третьей строки:
Делим третью строку на 0,125:
x + y + 1z = 25
7. Обратная подстановка:
z = 25
y = 0,5 - (0,5 * 25) = -12
x = 3,5 - (0,25 * -12) - (0,5 * 25) = -6
Итоговое решение:
x = -6
y = -12
z = 25
На следующем этапе второе уравнение нормализуется (делится на 2), что дает x + y + 0,5z = 0,5. Затем из третьего уравнения вычитается второе, умноженное на 0,75, чтобы исключить y. После этого третье уравнение упрощается до x + y + 0,125z = 3,125, а его нормализация (деление на 0,125) приводит к виду x + y + z = 25.
Обратная подстановка — завершающий этап метода Гаусса. Сначала из третьего уравнения находится значение z = 25. Это значение подставляется во второе уравнение, чтобы вычислить y: y = 0,5 – 0,5 * 25 = -12. Наконец, найденные y и z подставляются в первое уравнение для определения x: x = 3,5 – 0,25 * (-12) – 0,5 * 25 = -6.
Итоговое решение: x = -6, y = -12, z = 25. Эти значения удовлетворяют всем исходным уравнениям. Например, подстановка в третье уравнение: (-6) + (-12) + 25 = 7 — результат совпадает с заданным условием.
Практическое применение такого решения может быть связано с задачами, где требуется балансировка ресурсов. Например, если x, y, z — объемы материалов для производства, алгоритм помогает определить их оптимальное распределение при заданных ограничениях. Однако необычно большие значения z и отрицательные значения x и y указывают на то, что исходная система, возможно, моделирует гипотетическую ситуацию или требует проверки на корректность входных данных. В реальных условиях такие результаты могут сигнализировать о необходимости пересмотра условий задачи или уточнения коэффициентов.
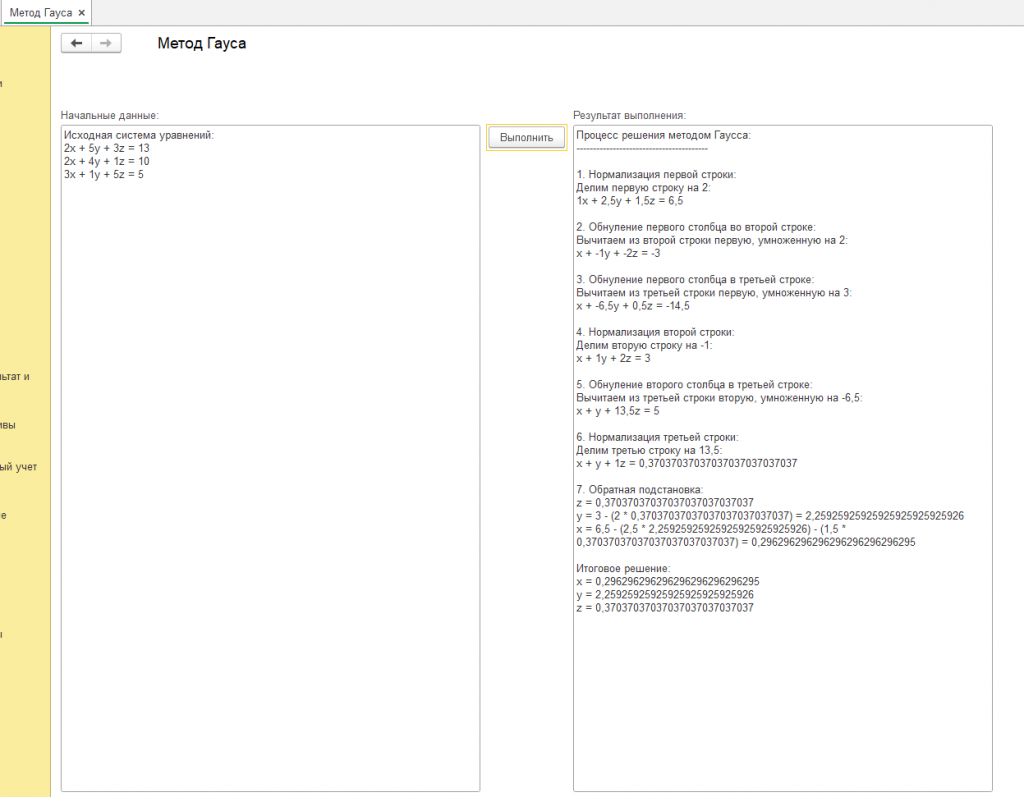
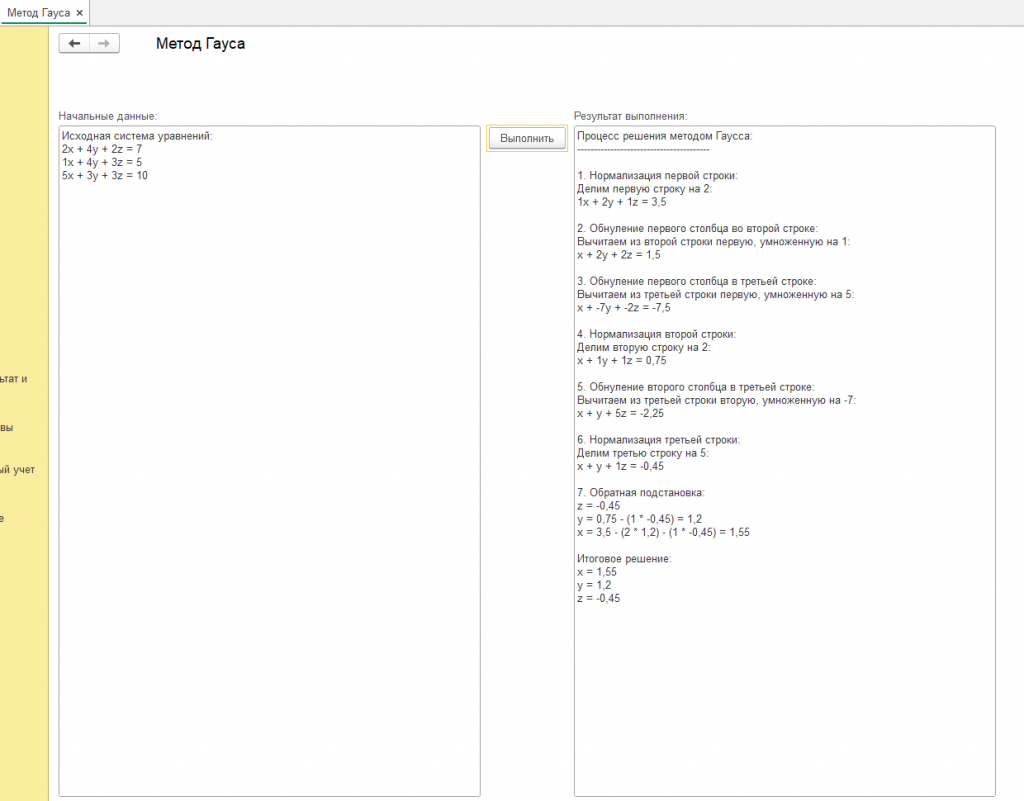
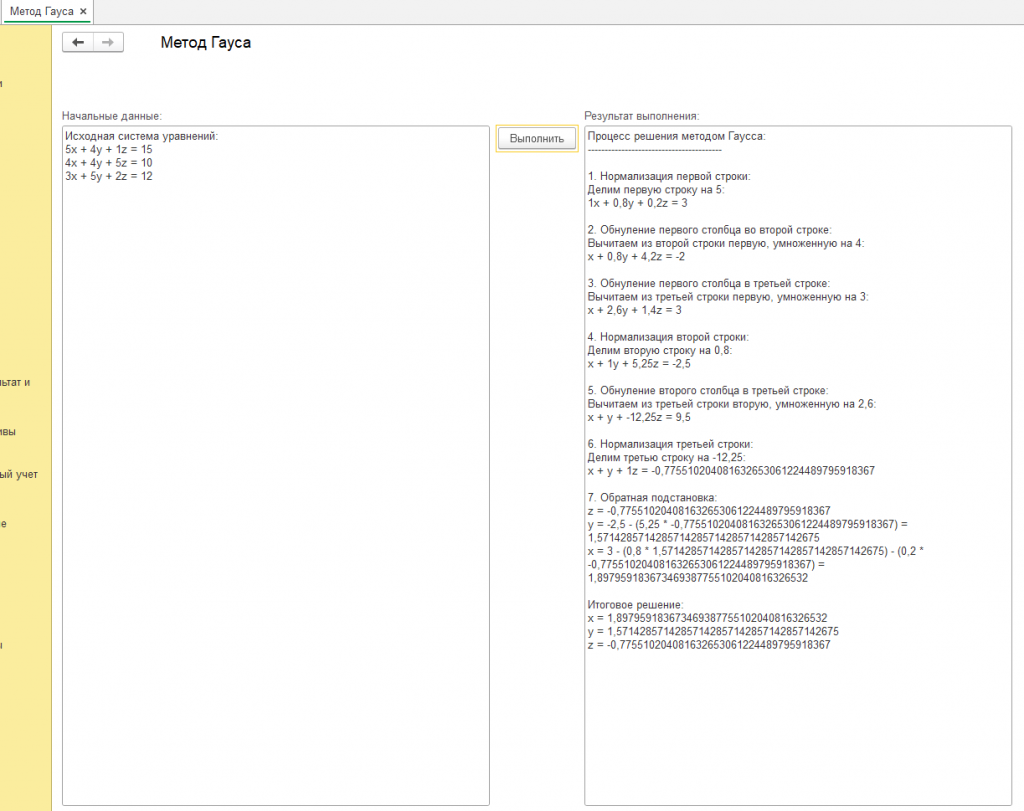
На других скриншотах (без надписи "пример") вы можете увидеть другие вычисленные значения алгоритмом Гауса при других начальных данных. Так же можете воспользоваться обработкой, код открыт, должна работать во всех 1с 8.3 и не только в erp.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.20.85
Вступайте в нашу телеграмм-группу Инфостарт