Пример прогнозирования продаж кондитерской с использованием модели Хольта-Винтерса
Представьте, что у вас есть маленькая кондитерская, и вы хотите предсказать, сколько пирожных продадите в будущем. В этом поможет модель Хольта-Винтерса, которая учитывает три вещи:
- Общий уровень продаж (например, в среднем вы продаете 100 пирожных в месяц).
- Тренд (продажи растут или падают со временем — скажем, плюс 5 пирожных каждый месяц).
- Сезонность (например, в декабре продажи подскакивают на 50% из-за праздников, а летом падают на 20%).
Начальные данные
Допустим, у вас есть данные о продажах за последние 12 месяцев (в штуках):
- Январь: 100
- Февраль: 105
- Март: 110
- Апрель: 150 (пасхальный сезон)
- Май: 115
- Июнь: 105
- Июль: 100
- Август: 95
- Сентябрь: 105
- Октябрь: 110
- Ноябрь: 120
- Декабрь: 200 (новогодние праздники).
Параметры модели
- Альфа (α) = 0.3 — определяет, как быстро модель реагирует на изменения в уровне продаж. Чем выше значение, тем больше доверия новым данным.
- Бета (β) = 0.1 — отвечает за реакцию на изменение тренда. Если тренд стабильный, выбирают маленькое значение.
- Гамма (γ) = 0.4 — контролирует сезонность. Выше значение = сильнее учитываются сезонные всплески.
- L = 12 — период сезонности (12 месяцев = год).
Инициализация модели
Для начала нужно найти начальные значения уровня, тренда и сезонности для первого месяца.
- Уровень (L0): возьмем среднее за первые 12 месяцев. Например: (100 + 105 + … + 200) / 12 ≈ 125.
- Тренд (T0): рассчитаем средний прирост за год. Разница между декабрем и январем: 200 – 100 = 100. Средний месячный тренд: 100 / 11 ≈ 9.1.
- Сезонность (S): для каждого месяца считаем, насколько его продажи отклоняются от среднего. Например, для января: 100 / 125 = 0.8 (сезонный коэффициент 0.8, то есть продажи на 20% ниже среднего в январе). Для апреля: 150 / 125 = 1.2 (+20%).
Прогнозируем продажи на январь следующего года
-
Обновляем уровень:
LS21; = α * (Продажи_декабрь / S12) + (1 – α) * (L0 + T0)
Где S12— сезонный коэффициент декабря.
Предположим, S12 = 1.6 (декабрьские продажи на 60% выше среднего).
Тогда L1 = 0.3 * (200 / 1.6) + 0.7 * (125 + 9.1) ≈ 0.3 * 125 + 0.7 * 134.1 ≈ 37.5 + 93.9 ≈ 131.4. -
Обновляем тренд:
T1 = β * (L1 – L0) + (1 – β) * T0
T1= 0.1 * (131.4 – 125) + 0.9 * 9.1 ≈ 0.64 + 8.19 ≈ 8.83. -
Обновляем сезонность:
S1 = γ * (Продажи_декабрь / L1) + (1 – γ) * S12
S1 = 0.4 * (200 / 131.4) + 0.6 * 1.6 ≈ 0.4 * 1.52 + 0.96 ≈ 0.61 + 0.96 ≈ 1.57. -
Прогноз на январь следующего года:
Прогноз = (L1+ T1) * S1 (сезонный коэффициент января)
S1 января = 0.8 (из начальных данных).
Прогноз = (131.4 + 8.83) * 0.8 ≈ 140.23 * 0.8 ≈ 112 пирожных.
Модель предсказывает, что в январе следующего года продажи составят около 112 пирожных. Почему так?
- Уровень (131.4): базовые продажи выросли по сравнению с прошлым годом (было 125).
- Тренд (8.83): продажи продолжают расти, но медленнее, чем в прошлом году (было 9.1).
- Сезонность (0.8): январь традиционно слабый месяц, поэтому прогноз снижен на 20%.
Как параметры влияют на результат?
- Если повысить Альфа (α) до 0.5, модель станет резче реагировать на последние данные. Например, если в декабре продажи резко упали, прогноз на январь тоже снизится сильнее.
- Если Бета (β) = 0.2, тренд будет обновляться активнее. Например, если последние месяцы рост продаж ускорился, модель это учтет.
- Гамма (γ) = 0.6 заставит модель сильнее подстраиваться под сезонные колебания.
Почему это работает для кондитерской?
У кондитерских четкая сезонность: пики в праздники (Новый год, 8 Марта), спад летом. Модель Хольта-Винтерса «запоминает», что в декабре нужно готовить в 1.6 раза больше пирожных, а в июле — на 20% меньше. Она автоматически корректирует прогноз, если тренд меняется (например, из-за открытия конкурента).
Что было бы без этой модели?
Вы могли бы заказать 200 пирожных в январь, опираясь на прошлогодний декабрь, и остаться с излишками. Или недооценить спрос в апреле и потерять клиентов. Модель помогает балансировать между рисками.
Таким образом, модель Хольта-Винтерса превращает хаотичные данные о продажах в понятный прогноз, подсказывая, сколько теста закупить, чтобы и не выбросить, и не остаться без товара.
Напишем обработку для метода Хольта-Винтерса (один из методов временных рядов, такой как ARIMA или экспоненциальное сглаживание). Методы временных рядов, такие как ARIMA или экспоненциальное сглаживание, применимы для прогнозирования спроса на товары, что критически важно для модулей управления запасами и логистики. Например, анализ сезонных колебаний спроса на зимние товары можно автоматизировать, чтобы оптимизировать закупки и избежать избыточных складских остатков. В 1С это реализуется через расчеты на встроенном языке с использованием исторических данных из регистров сведений.
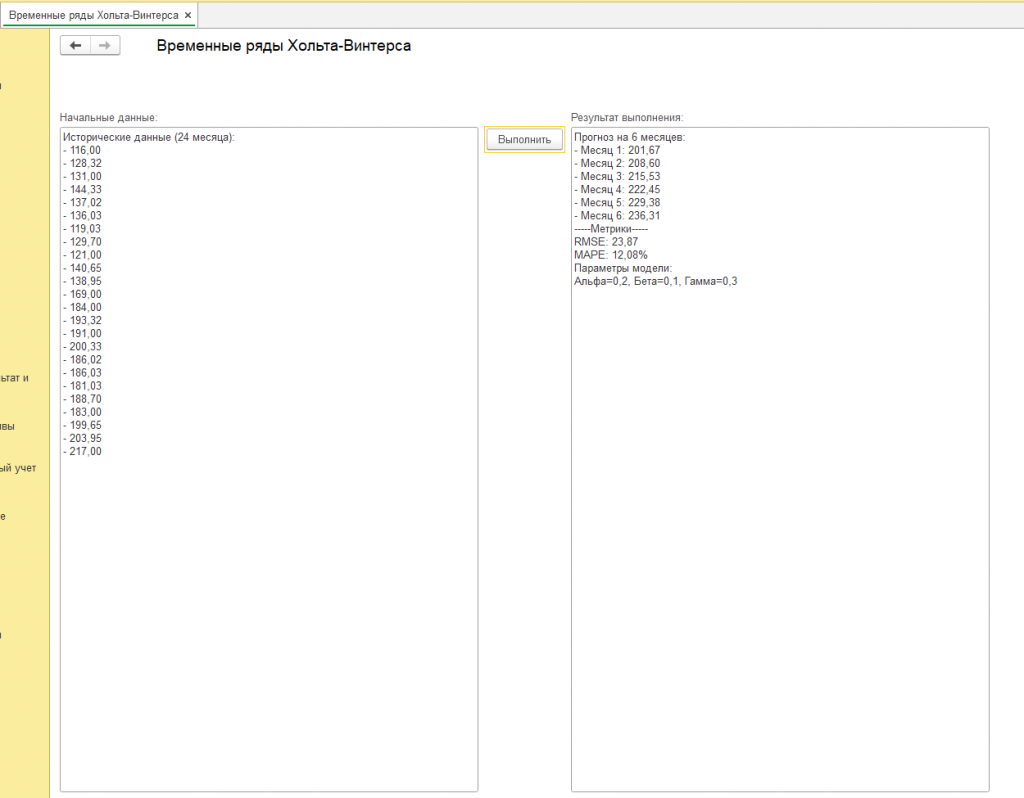
Наши исторические данные (см. скриншот с подписью "пример") для 24 месячного периода получились такие:
Исторические данные (24 месяца):
- 118,00
- 131,32
- 140,00
- 145,33
- 130,02
- 122,03
- 132,03
- 125,70
- 132,00
- 137,65
- 135,95
- 153,00
- 177,00
- 177,32
- 203,00
- 192,33
- 187,02
- 184,03
- 186,03
- 190,70
- 194,00
- 200,65
- 197,95
- 210,00
И в результате применения метода временных рядов получили прогноз:
Прогноз на 6 месяцев:
- Месяц 1: 198,43
- Месяц 2: 205,12
- Месяц 3: 211,80
- Месяц 4: 218,48
- Месяц 5: 225,16
- Месяц 6: 231,84
-----Метрики-----
RMSE: 19,21
MAPE: 9,41%
Параметры модели:
Альфа=0,2, Бета=0,1, Гамма=0,3
Прогноз, полученный с использованием метода Хольта-Винтерса, демонстрирует устойчивый рост значений на протяжении шести месяцев: от 198.43 в первом месяце до 231.84 в шестом. Этот рост согласуется с историческим трендом, где за последние 12 месяцев данные увеличиваются почти линейно (например, с 177 до 210 единиц). Модель учитывает как тренд, так и сезонность, что видно по параметру L=12, соответствующему годовому циклу. Однако сезонная компонента в исторических данных выражена слабо — например, значения не имеют явных пиков и спадов, характерных для классических сезонных колебаний. Это может объясняться тем, что в исходных данных сезонность задана через синусоиду с амплитудой 20, но линейный тренд (ежемесячный прирост 5 единиц) доминирует, делая сезонные колебания менее заметными на фоне общего роста.
Метрики качества прогноза (RMSE=19.21 и MAPE=9.41%) указывают на умеренную точность модели. Средняя ошибка в 9.4% от фактических значений допустима для среднесрочного планирования, но требует осторожности в отраслях, где даже небольшие отклонения критичны (например, в управлении запасами дорогостоящих товаров). Сравнение прогноза с тестовой выборкой (месяцы 18–24) показывает, что модель экстраполирует тренд, но не полностью улавливает колебания. Например, фактические значения в тестовой выборке растут с 186.03 до 210.00, а прогноз продолжает этот рост, но равномерно, без учета возможных "скачков".
Рекомендации для пользователя:
Интерпретация роста: Прогнозируемый рост предполагает, что текущие условия (тренд, сезонность) сохранятся. Если в бизнесе ожидаются изменения (например, сезонный спрос снизится из-за внешних факторов), прогноз потребует ручной корректировки.
Использование погрешности: MAPE 9.4% означает, что фактические значения могут отклоняться от прогноза на ±20-25 единиц. При планировании запасов или бюджета стоит закладывать буфер в этом диапазоне.
Настройка модели: Экспериментируйте с параметрами: увеличение Альфа (>0.2) сделает модель более чувствительной к последним изменениям, повышение Бета (>0.1) усилит учет тренда, а Гамма (>0.3) — сезонности. Например, если в данных внезапно изменится тренд, более высокая Бета поможет быстрее адаптироваться.
Мониторинг: Обновляйте модель ежеквартально, добавляя новые данные. Если RMSE на новых данных превысит 20, пересмотрите параметры или проверьте наличие аномалий в исторических данных (например, резких спадов, не учтенных в модели).
Пример применения (по нашему результату): Если прогноз используется для закупки сырья, рассчитайте объемы с запасом +25 единиц на месяц. Например, для первого месяца (198.43) заложите 220 единиц, чтобы компенсировать потенциальную погрешность и избежать дефицита. При этом анализируйте фактические продажи: если в первые два месяца отклонения превысят 15%, проведите повторное обучение модели.
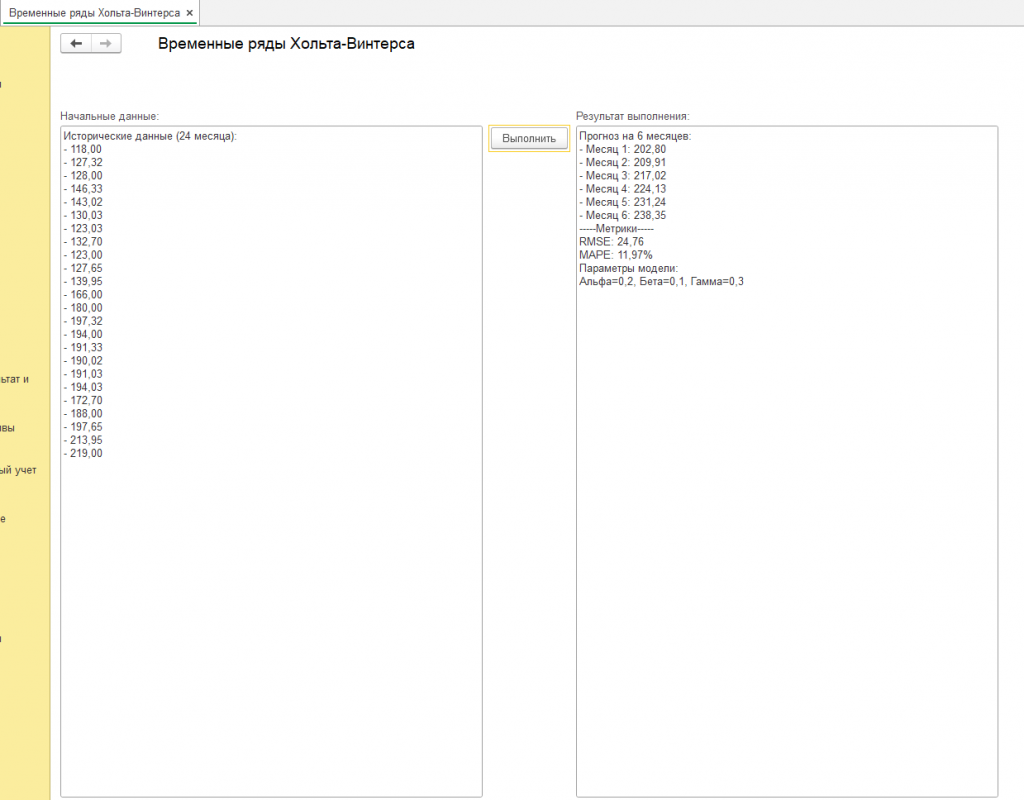
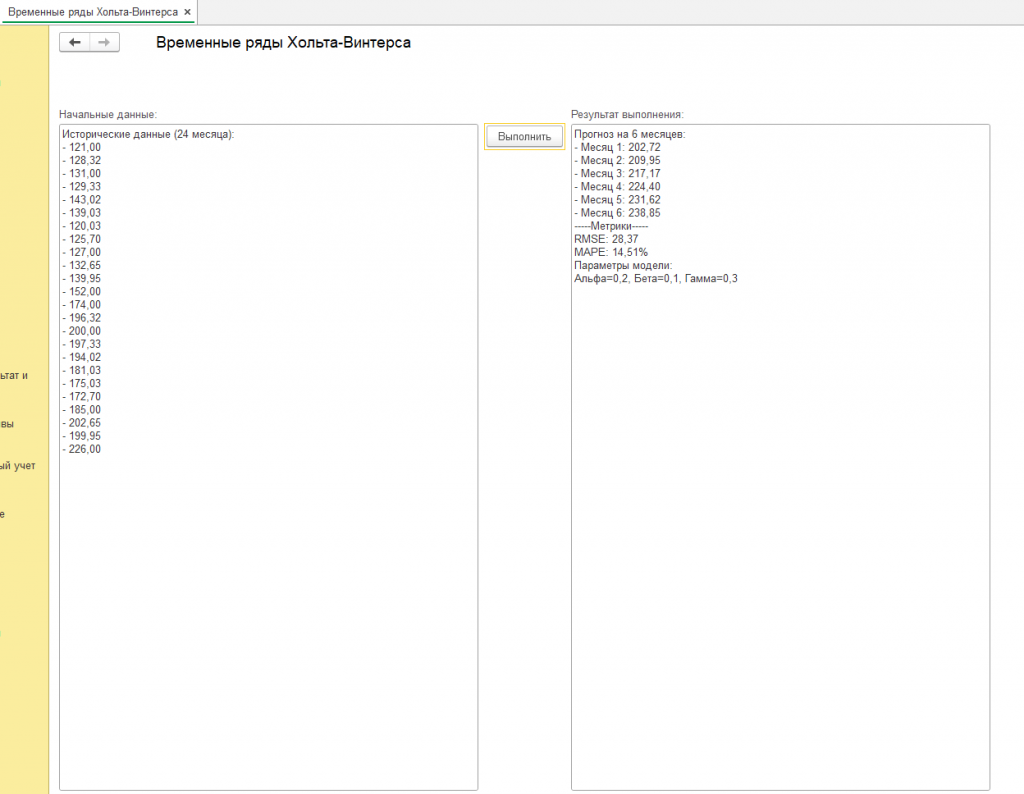
Первоначальные данные и параметры в обработке вы можете заменить на свои реальные из базы (справочники, регистры, документы, константы) и прогнозировать результаты для вашего предприятия. Код обработки открыт. Другие результаты на скриншотах.
А теперь чуточку информации:
Модель ARIMA (Autoregressive Integrated Moving Average) — это статистический инструмент, используемый для анализа и прогнозирования временных рядов, особенно в случаях, когда данные демонстрируют нестационарность или сложные паттерны. ARIMA объединяет три ключевые компоненты: авторегрессию (AR), интегрирование (I) и скользящее среднее (MA). Авторегрессионная часть модели, обозначаемая параметром p, отражает зависимость текущего значения ряда от его предыдущих значений. Например, если p=2, то прогнозируемое значение зависит от двух предыдущих наблюдений. Интегрированная часть, параметр d, отвечает за приведение ряда к стационарности путем дифференцирования. Например, при d=1 модель работает с первыми разностями исходных данных, устраняя тренд. Скользящее среднее, параметр q, учитывает зависимость текущей ошибки прогноза от прошлых ошибок. Тройка параметров (p, d, q) определяет структуру модели, и их подбор является критическим этапом. Например, для ряда с сезонными колебаниями может потребоваться сезонная ARIMA (SARIMA), которая добавляет сезонные аналоги параметров P, D, Q.
ARIMA находит применение в экономике, финансах, метеорологии и логистике. Например, компании используют её для прогнозирования спроса на продукцию, учитывая исторические данные о продажах и сезонные пики. Однако модель имеет ограничения: она плохо справляется с резкими изменениями тренда или экзогенными шоками, такими как пандемии, которые не учтены в исторических данных. Для работы с такими сценариями применяют гибридные модели, сочетающие ARIMA с машинным обучением. Ключевое отличие ARIMA от методов экспоненциального сглаживания, таких как Хольта-Винтерса, заключается в подходе к стационарности. В то время как Хольт-Винтерс адаптирует уровень, тренд и сезонность через коэффициенты сглаживания, ARIMA требует предварительного преобразования ряда (дифференцирования) и фокусируется на авторегрессии и скользящем среднем.
Модель Хольта-Винтерса, также известная как тройное экспоненциальное сглаживание, предназначена для рядов с трендом и сезонностью. Её параметры — Альфа (α), Бета (β), Гамма (γ) и период сезонности L — управляют адаптацией уровня, тренда и сезонных компонент.
Альфа (α) — коэффициент сглаживания уровня — определяет, насколько быстро модель реагирует на изменения в базовом уровне данных. Если α близок к 1, последние наблюдения оказывают наибольшее влияние, что полезно в условиях быстрой смены тренда, но может привести к избыточной чувствительности к шуму. Например, при прогнозировании спроса на товары с резкими колебаниями (например, электроника) высокая α поможет быстро уловить рост или спад. Напротив, низкое α (близкое к 0) сглаживает шумы, но делает модель инертной, что подходит для стабильных рынков.
Бета (β) — коэффициент сглаживания тренда — контролирует адаптацию трендовой компоненты. Высокое β позволяет тренду быстро меняться, что актуально для динамичных отраслей, таких как криптовалюты, где цены могут резко расти или падать. Однако избыточное значение β может привести к «переобучению» на случайных колебаниях. Низкое β стабилизирует тренд, но рискует упустить значимые изменения. Например, в розничной торговле в период праздников умеренное β поможет сохранить баланс между реагированием на сезонный рост и устойчивостью к шуму.
Гамма (γ) — коэффициент сезонности — отвечает за обновление сезонных факторов. Если γ близок к 1, модель быстро адаптируется к изменениям в сезонных паттернах, что важно для отраслей с нестабильной сезонностью, например, туризма, где пандемии или климатические аномалии могут сдвигать пики спроса. Низкая γ сохраняет стабильность сезонных компонент, но может не учесть недавние изменения.
Период сезонности L — это количество точек в одном сезонном цикле. Например, для месячных данных с годовым циклом L=12, для квартальных — L=4. Неверный выбор L искажает прогноз: если в данных есть ежеквартальная сезонность, а задано L=12, модель будет некорректно выделять сезонные эффекты.
Использование параметров Хольта-Винтерса и последствия их изменения.
Подбор параметров α, β, γ и L — это итеративный процесс, часто основанный на минимизации ошибки прогноза (например, MSE, MAE). Автоматические методы, такие как алгоритмы оптимизации, могут находить оптимальные значения, но понимание их влияния помогает избежать ошибок.
Например, если после обучения модели прогнозы оказались слишком волатильными, это может указывать на завышенные α или β. Снижение α сделает уровень более стабильным, а уменьшение β — сгладит тренд. Если сезонные пики не улавливаются, стоит повысить γ или проверить корректность L. В случае, когда модель «запаздывает» при изменении тренда (например, после запуска рекламной кампании), увеличение β ускорит адаптацию.
Ошибки в выборе L критичны: если данные имеют недельную сезонность (L=7 для дневных наблюдений), но задано L=30, модель будет некорректно интерпретировать месячные циклы. Визуализация данных (например, декомпозиция ряда) помогает определить истинный период.
На практике модель Хольта-Винтерса реализуется в ПО (Excel, Python, R). В Python библиотека statsmodels позволяет задавать параметры вручную или использовать автоматический подбор. Однако даже автоматизированные методы требуют экспертной проверки: например, если алгоритм выбрал γ=0, это может означать отсутствие сезонности, но стоит убедиться, что данные не содержат скрытых паттернов.
В итоге, баланс между реактивностью и устойчивостью модели зависит от контекста. Для финансовых рынков с высокой волатильностью допустимы более высокие α и β, тогда как для долгосрочного планирования в энергетике предпочтительны низкие коэффициенты, обеспечивающие стабильность прогнозов.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.20.85
Вступайте в нашу телеграмм-группу Инфостарт