Метод Монте-Карло
Имеем
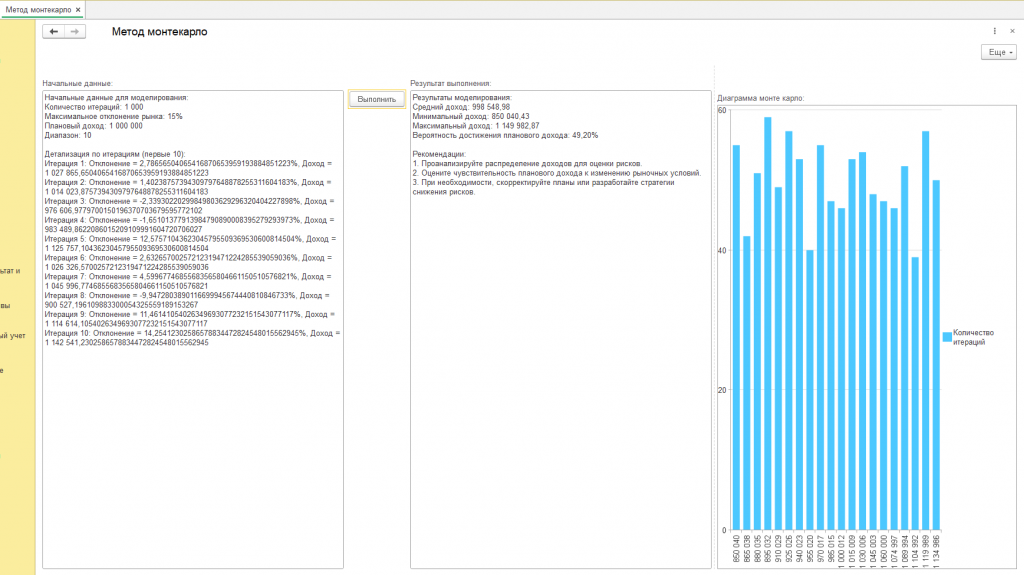
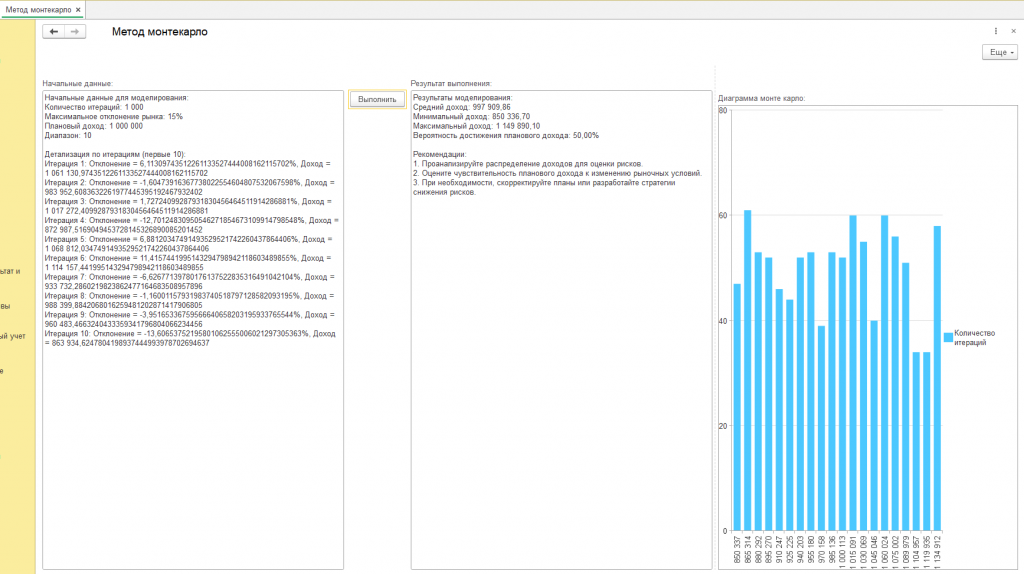
Начальные данные для моделирования:
Количество итераций: 1 000
Максимальное отклонение рынка: 15%
Плановый доход: 1 000 000
Диапазон: 10
Детализация по итерациям (первые 10):
Итерация 1: Отклонение = 2,65034255284125510436511950203336765%, Доход = 1 026 503,4255284125510436511950203336765
Итерация 2: Отклонение = 0,47754336741695724600389535678641298%, Доход = 1 004 775,4336741695724600389535678641298
Итерация 3: Отклонение = -14,21388403727064934495618784449905804%, Доход = 857 861,1596272935065504381215550094196
Итерация 4: Отклонение = -9,91932053931972955803380570328650199%, Доход = 900 806,7946068027044196619429671349801
Итерация 5: Отклонение = 13,61879837434245235620589283206637316%, Доход = 1 136 187,9837434245235620589283206637316
Итерация 6: Отклонение = 1,58601077892491844923349992587079757%, Доход = 1 015 860,1077892491844923349992587079757
Итерация 7: Отклонение = -9,45467955070889544456938641252214703%, Доход = 905 453,2044929110455543061358747785297
Итерация 8: Отклонение = 6,82240335546024221821228093891690506%, Доход = 1 068 224,0335546024221821228093891690506
Итерация 9: Отклонение = -0,02468327642993146470513461732890797%, Доход = 999 753,1672357006853529486538267109203
Итерация 10: Отклонение = 2,5373718974966024741289677270988393%, Доход = 1 025 373,718974966024741289677270988393
и результат:
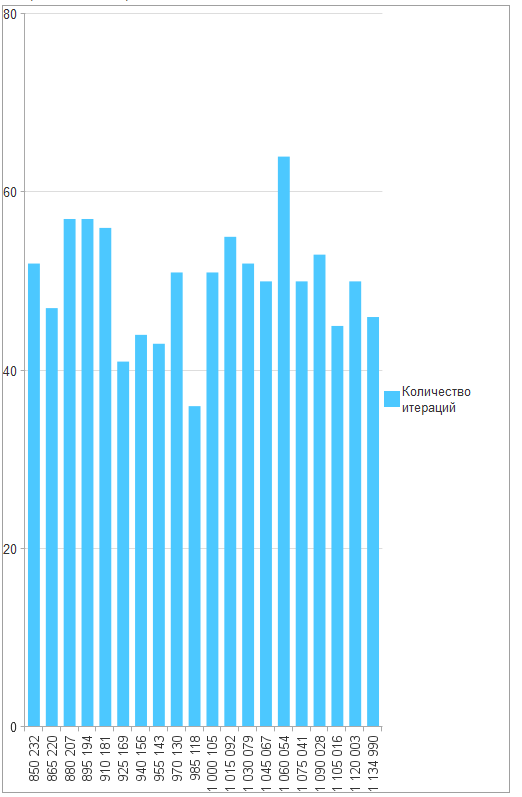
Результаты моделирования:
Средний доход: 1 000 079,38
Минимальный доход: 850 232,39
Максимальный доход: 1 149 977,40
Вероятность достижения планового дохода: 51,80%
Рекомендации:
1. Проанализируйте распределение доходов для оценки рисков.
2. Оцените чувствительность планового дохода к изменению рыночных условий.
3. При необходимости, скорректируйте планы или разработайте стратегии снижения рисков.
Модель простая и предполагает независимость и случайность отклонений рынка. В реальности, рыночные условия часто взаимосвязаны, и могут иметь более сложные зависимости во времени.
Метод Монте-Карло сработал корректно, но результаты нельзя считать окончательными из-за малого количества итераций. Для получения более надежных результатов необходимо: увеличить количество итераций: Запустите моделирование с гораздо большим количеством итераций. 1000 итераций — это мало для получения высокой точности результатов. Чем больше итераций, тем точнее будет оценка среднего дохода и вероятности. Рекомендуется увеличить количество итераций до 10000 или 100000 для более надежных результатов.
Положительные моменты:
- Средний доход близок к планируемому: Средний доход (1 000 079,38) очень близок к запланированному (1 000 000). Это хороший признак того, что модель работает корректно. Небольшое отклонение является нормальным для метода Монте-Карло.
- Диапазон отклонений: Отклонения в данных по итерациям находятся в пределах, заданных параметром “Максимальное отклонение рынка” (15%).
- Вероятность достижения планового дохода: Вероятность 51,8% расположена близко к 50%, что ожидаемо при симметричном распределении отклонений.
1. Введение в методы Монте-Карло и их роль в управлении рисками
Методы Монте-Карло представляют собой класс вычислительных алгоритмов, основанных на многократном случайном моделировании для получения численных результатов. Их название происходит от знаменитого казино в Монте-Карло, символизирующего случайность и вероятность, что подчеркивает их фундаментальную связь с теорией вероятностей. Впервые эти методы были применены в середине XX века при разработке ядерного оружия в рамках Манхэттенского проекта, где требовалось решать сложные задачи, связанные с нейтронной диффузией.
Современное применение методов Монте-Карло охватывает широкий спектр областей, включая физику, инженерию, биологию и, что особенно важно, финансы. В контексте управления рисками они используются для оценки вероятности достижения определенных финансовых показателей в условиях неопределенности рыночной среды. Традиционные аналитические методы, такие как детерминированное моделирование, часто оказываются недостаточно гибкими для учета всех возможных сценариев, особенно в условиях высокой волатильности рынка.
Одним из ключевых преимуществ методов Монте-Карло является их способность учитывать нелинейные зависимости и сложные взаимодействия между переменными. Например, при прогнозировании доходности инвестиционного портфеля можно смоделировать тысячи возможных траекторий изменения цен активов, учитывая их корреляцию, волатильность и другие факторы. Это позволяет получить не только точечные оценки, но и распределение вероятностей, что крайне важно для принятия обоснованных решений.
Однако, несмотря на свою универсальность, методы Монте-Карло требуют значительных вычислительных ресурсов, особенно при работе с большими объемами данных. Кроме того, их точность напрямую зависит от качества генерации случайных чисел и адекватности выбранной модели.
Математические основы методов Монте-Карло и их адаптация к финансовым моделям
Математический аппарат методов Монте-Карло базируется на теории вероятностей и статистическом анализе, что обеспечивает их универсальность в моделировании стохастических процессов. Ключевым элементом является генерация псевдослучайных чисел, имитирующих поведение рыночных переменных, таких как цены активов, процентные ставки или объемы продаж. Для этого используются алгоритмы, преобразующие равномерно распределенные случайные величины (например, с помощью линейного конгруэнтного метода) в значения, соответствующие заданным распределениям — нормальному, логнормальному, Пуассона и другим. Выбор распределения определяется природой моделируемого параметра: например, логнормальное распределение часто применяется для описания динамики цен на акции, чтобы исключить отрицательные значения и учесть асимметрию доходностей.
Важным аспектом является учет корреляций между переменными, что особенно актуально в финансовых системах, где изменения одних показателей тесно связаны с другими. Для моделирования зависимостей используется метод копулы или преобразование Холецкого, позволяющее генерировать многомерные случайные векторы с заданной матрицей корреляций. Это обеспечивает адекватное отражение рыночных взаимосвязей, таких как зависимость между курсами валют и ценами на сырьевые товары. Однако сложность возрастает при работе с большим числом переменных, что требует оптимизации вычислительных ресурсов и применения методов снижения дисперсии, таких как стратифицированная выборка или контрольные переменные.
Оценка точности результатов Монте-Карло — еще один критический этап. Поскольку метод основан на статистике, ключевым показателем является стандартная ошибка, которая уменьшается пропорционально квадратному корню из числа итераций. На практике это означает, что для повышения точности прогноза в два раза необходимо увеличить объем выборки в четыре раза, что может быть ресурсоемко. Для преодоления этого ограничения применяются квази-Монте-Карло методы, использующие детерминированные последовательности с низкой дискрепцией (например, последовательности Соболя), которые обеспечивают более равномерное покрытие пространства параметров и ускоренную сходимость.
Интеграция методов Монте-Карло в финансовые модели требует также учета специфики бюджетного планирования. Например, при оценке вероятности достижения плановой прибыли необходимо смоделировать не только внешние рыночные факторы, но и внутренние переменные, такие как операционные издержки или эффективность управления. Здесь возникает задача балансировки между детализацией модели и ее вычислительной сложностью. Упрощение модели может привести к игнорированию важных рисков, в то время как избыточная детализация затрудняет интерпретацию результатов. Решением становится иерархическое моделирование, при котором ключевые факторы риска выделяются на верхнем уровне, а второстепенные — агрегируются в виде поправочных коэффициентов.
Переход к практическому применению методов Монте-Карло в бюджетных модулях подразумевает их адаптацию к существующим IT-инфраструктурам. Современные платформы финансового анализа, такие как MATLAB, Python (с библиотеками NumPy и SciPy) или специализированное ПО (например, @RISK), предоставляют инструменты для автоматизации генерации сценариев и визуализации результатов. Однако успешная реализация зависит от качества исходных данных, включая исторические ряды и экспертные оценки, которые служат основой для калибровки моделей. Это подчеркивает необходимость междисциплинарного подхода, объединяющего аналитиков, экономистов и IT-специалистов.
Практические кейсы применения методов Монте-Карло в бюджетном планировании
Реализация методов Монте-Карло в бюджетных модулях демонстрирует свою эффективность через конкретные примеры, где неопределенность рыночных условий напрямую влияет на финансовые результаты. Одним из таких кейсов является оценка вероятности достижения целевой рентабельности инвестированного капитала (ROIC) в условиях волатильности сырьевых рынков. Компания, работающая в секторе металлургии, может столкнуться с непредсказуемыми колебаниями цен на железную руду, что существенно влияет на себестоимость продукции. Применение Монте-Карло позволяет смоделировать тысячи сценариев изменения цен, учитывая историческую волатильность и корреляции с другими факторами, такими как курс национальной валюты. В результате руководство получает не только ожидаемое значение ROIC, но и доверительные интервалы, например, с вероятностью 95% рентабельность составит от 8% до 15%. Это создает основу для формирования резервов или пересмотра ценовой политики.
Еще одним примером служит стресс-тестирование бюджета на предмет экстремальных событий, таких как экономические кризисы или природные катаклизмы. Традиционные подходы, основанные на исторических данных, часто недооценивают риски «черных лебедей», поскольку такие события редки и плохо предсказуемы. Методы Монте-Карло позволяют искусственно генерировать сценарии с экстремальными значениями ключевых параметров (например, падение ВВП на 10% или скачок инфляции до 20%), оценивая их влияние на ликвидность и платежеспособность компании. Это помогает выявить «узкие места» в бюджете, такие как недостаточный объем кредитной линии или зависимость от единственного поставщика, и разработать превентивные меры.
Важным направлением является также оптимизация распределения ресурсов между проектами в условиях ограниченного финансирования. Например, венчурный фонд, выбирающий стартапы для инвестирования, сталкивается с неопределенностью в оценке их будущей доходности. Моделирование Монте-Карло позволяет оценить распределение возможных возвратов для каждого проекта, учитывая вероятность успеха, сроки выхода на рынок и конкуренцию. На основе этих данных строится эффективная граница риска и доходности, что помогает сбалансировать портфель между высокорисковыми и стабильными активами. При этом учитывается не только математическое ожидание прибыли, но и такие метрики, как Value at Risk (VaR) или Conditional Value at Risk (CVaR), которые количественно оценивают потенциальные потери.
Однако успех применения методов Монте-Карло зависит от корректной интерпретации результатов. Распространенной ошибкой является смещение фокуса на «средние» значения, игнорируя хвосты распределений, где сосредоточены критические риски. Например, модель может показать 70% вероятность достижения плановой выручки, но при этом в 5% сценариев возможен убыток, превышающий допустимые лимиты. Для минимизации таких рисков необходима интеграция Монте-Карло с системами риск-менеджмента, включая установление лимитов потерь и разработку сценариев реагирования.
Переходя к заключительной части, стоит отметить, что дальнейшее развитие методов Монте-Карло связано с интеграцией искусственного интеллекта и машинного обучения. Эти технологии позволяют автоматизировать выбор распределений, уточнять корреляции в реальном времени и адаптировать модели к изменяющимся рыночным условиям, что открывает новые горизонты для повышения точности бюджетного планирования.
Интеграция искусственного интеллекта, этические аспекты и заключение
Развитие методов Монте-Карло в контексте финансового моделирования неразрывно связано с прогрессом в области искусственного интеллекта (ИИ) и машинного обучения (МО). Современные алгоритмы, такие как нейронные сети с глубоким обучением, позволяют автоматизировать выбор распределений вероятностей для входных параметров, что традиционно являлось одной из наиболее субъективных и трудоемких задач. Например, анализ больших данных о рыночных транзакциях с помощью МО может выявить скрытые паттерны волатильности или корреляции между активами, которые не поддаются описанию стандартными статистическими методами. Интеграция этих технологий с Монте-Карло открывает возможность создания самообучающихся моделей, адаптирующихся к изменяющимся рыночным условиям в режиме реального времени. Такие системы способны пересчитывать вероятностные прогнозы при поступлении новых данных, снижая запаздывание в принятии решений.
Однако внедрение ИИ в методы Монте-Карло сталкивается с рядом методологических и этических вызовов. Во-первых, «черный ящик» нейронных сетей затрудняет интерпретацию результатов, что критично в условиях регулируемых отраслей, где требуется прозрачность расчетов. Во-вторых, существует риск переобучения моделей на исторических данных, что может привести к недооценке редких, но катастрофических событий. Эти проблемы актуализируют необходимость разработки гибридных подходов, сочетающих экспертные знания с возможностями ИИ. Например, байесовские методы позволяют включать априорные ожидания аналитиков в процесс обучения алгоритмов, обеспечивая баланс между данными и экспертизой.
Этические аспекты применения Монте-Карло также заслуживают внимания. Автоматизация решений на основе вероятностных моделей может привести к делегированию ответственности за финансовые последствия алгоритмам, что ставит вопрос о справедливости и подотчетности. Например, модель, рекомендующая сокращение штата для минимизации рисков ликвидности, должна учитывать не только математические ожидания, но и социальные последствия. В этой связи важно внедрять принципы ответственного ИИ, включая аудит моделей на предмет дискриминации, а также создание механизмов человеческого контроля над критическими решениями.
В заключение, методы Монте-Карло остаются незаменимым инструментом для управления финансовыми рисками в условиях растущей сложности рынков. Их эволюция от математического аппарата к интегрированным системам анализа данных отражает общий тренд цифровизации экономики. Однако дальнейший прогресс требует решения технических, методологических и этических вопросов. Совершенствование алгоритмов генерации сценариев, интеграция с МО и развитие регуляторных рамок позволят повысить точность прогнозов и минимизировать риски как для бизнеса, так и для общества. В конечном итоге, успех применения методов Монте-Карло будет зависеть от способности сочетать технологические инновации с глубоким пониманием природы рисков и человеческих ценностей.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.20.85
Вступайте в нашу телеграмм-группу Инфостарт