Эконометрическое наследие Питера Робинсона: от непараметрики к полупараметрическим моделям и анализу временных рядов

Эконометрический анализ в контексте работ Питера Робинсона: непараметрический подход к исследованию взаимосвязей

   Вклад Питера Робинсона в развитие эконометрики трудно переоценить, особенно в области непараметрических и полупараметрических методов. Его работы открыли новые горизонты для анализа данных, позволяя исследователям избегать жестких предположений о форме распределений и функциональных зависимостях. В настоящем исследовании мы попытаемся проиллюстрировать некоторые аспекты непараметрического подхода, вдохновленные идеями Робинсона, на примере искусственно сгенерированных данных. Цель состоит не в том, чтобы повторить конкретные результаты Робинсона, а в том, чтобы продемонстрировать возможности и особенности непараметрических методов в контексте анализа взаимосвязей между переменными.

   Для достижения этой цели мы сгенерировали искусственные данные для двух переменных, условно обозначенных как X и Y (см. скриншот с подписью "пример"). Этот шаг является необходимым для того, чтобы иметь полный контроль над структурой данных и иметь возможность оценить, насколько хорошо непараметрические методы справляются с выявлением скрытых закономерностей. В реальных экономических исследованиях, где данные часто зашумлены и искажены, эта способность особенно ценна.

   Параметры генерации данных были заданы следующим образом. Размер выборки, то есть количество наблюдений, составил 100. Это число представляется достаточным для того, чтобы продемонстрировать основные принципы непараметрического анализа, не прибегая к слишком сложным вычислительным процедурам. Для переменной X значения генерировались в диапазоне от 10 до 100. Этот диапазон был выбран произвольно, но он позволяет охватить достаточно широкий спектр возможных значений переменной, что важно для обеспечения репрезентативности выборки. Аналогично, для переменной Y значения генерировались в диапазоне от 5 до 50. Как и в случае с переменной X, этот диапазон был выбран исходя из соображений практической целесообразности и необходимости обеспечения достаточной вариативности данных.

   Сгенерированные данные представлены в виде массивов, содержащих индивидуальные значения переменных X и Y. Эти массивы являются отправной точкой для дальнейшего анализа. Визуальное представление данных в виде графиков рассеяния или гистограмм могло бы предоставить дополнительную информацию о структуре данных, однако в рамках данного исследования мы ограничимся только числовым анализом.

   Следует отметить, что использование искусственно сгенерированных данных имеет как преимущества, так и недостатки. С одной стороны, это позволяет нам контролировать параметры генерации данных и точно знать, какие закономерности мы должны обнаружить. С другой стороны, искусственные данные могут не отражать всей сложности и разнообразия реальных экономических данных, что ограничивает обобщаемость полученных результатов. Тем не менее, для целей иллюстрации основных принципов непараметрического анализа, использование искусственных данных представляется вполне оправданным.

   Важно подчеркнуть, что подход Питера Робинсона к эконометрике характеризуется стремлением к минимизации предположений о форме распределений и функциональных зависимостях. Это особенно важно в ситуациях, когда теоретические соображения не позволяют сделать однозначные выводы о виде этих распределений и зависимостей. Непараметрические методы, в отличие от параметрических, не требуют задания конкретных функциональных форм и позволяют оценивать зависимости на основе самих данных.

   В рамках данного исследования мы сосредоточимся на одном из наиболее распространенных непараметрических методов – оценке плотности распределения с использованием ядра Гаусса. Этот метод позволяет оценить плотность вероятности переменной X в каждой точке ее диапазона значений, не делая никаких предположений о форме этой плотности. Ядро Гаусса играет роль сглаживающей функции, которая позволяет усреднить значения переменной X в окрестности каждой точки и получить более гладкую оценку плотности.

   Выбор ширины окна (параметра сглаживания) является критически важным для получения адекватной оценки плотности. Слишком маленькая ширина окна приведет к зашумленной оценке, которая будет отражать только случайные колебания данных. Слишком большая ширина окна, наоборот, приведет к пересглаженной оценке, которая скроет важные детали структуры распределения. Существуют различные методы выбора оптимальной ширины окна, такие как метод кросс-валидации или метод plug-in. Однако в рамках данного исследования мы ограничимся фиксированным значением ширины окна, выбранным исходя из соображений практической целесообразности.

   Для иллюстрации работы непараметрического метода оценки плотности мы выберем точку оценки, равную 55. Эта точка находится примерно в середине диапазона значений переменной X и представляется достаточно репрезентативной для оценки плотности в этой области. Ширина окна (параметр сглаживания) будет установлена равной 5. Это значение было выбрано на основе предварительного анализа данных и представляется разумным компромиссом между необходимостью сглаживания случайных колебаний и сохранением важных деталей структуры распределения.

   После того, как все параметры были заданы, мы можем приступить к расчету непараметрической оценки плотности переменной X в точке 55 с использованием ядра Гаусса. Этот расчет включает в себя суммирование значений ядра Гаусса, вычисленных для каждого наблюдения в выборке, с учетом расстояния между этим наблюдением и точкой оценки. Полученное значение оценки плотности будет отражать относительную частоту встречаемости значений переменной X в окрестности точки 55.

   Однако, прежде чем перейти к интерпретации полученного результата, необходимо провести расчет основных статистических показателей для каждой переменной. Это позволит нам получить общее представление о структуре данных и оценить, насколько хорошо непараметрический метод оценки плотности согласуется с параметрическими оценками. В частности, мы рассчитаем среднее значение и дисперсию для каждой переменной.

   Среднее значение является мерой центральной тенденции и показывает среднее значение переменной в выборке. Дисперсия, напротив, является мерой разброса и показывает, насколько сильно значения переменной отклоняются от среднего значения. Эти две меры являются важными индикаторами структуры данных и позволяют нам получить общее представление о распределении переменных.

   В дополнение к среднему значению и дисперсии мы также рассчитаем коэффициент корреляции Пирсона между переменными X и Y. Этот коэффициент является мерой линейной связи между двумя переменными и показывает, насколько сильно они изменяются вместе. Значение коэффициента корреляции может варьироваться от -1 до +1. Значение +1 указывает на сильную положительную линейную связь, значение -1 указывает на сильную отрицательную линейную связь, а значение 0 указывает на отсутствие линейной связи.

   Важно отметить, что коэффициент корреляции Пирсона является мерой только линейной связи и не может выявить нелинейные зависимости между переменными. Поэтому, даже если коэффициент корреляции равен нулю, это не означает, что между переменными нет никакой связи. В этом случае необходимо использовать другие методы анализа, такие как непараметрические методы или методы машинного обучения.

   После того, как все необходимые статистические показатели были рассчитаны, мы можем приступить к интерпретации полученных результатов. Прежде всего, мы проанализируем значения среднего значения и дисперсии для каждой переменной. Это позволит нам получить общее представление о структуре данных и оценить, насколько хорошо наши данные соответствуют нашим ожиданиям.

   Затем мы проанализируем значение коэффициента корреляции Пирсона между переменными X и Y. Это позволит нам оценить, существует ли какая-либо линейная связь между этими переменными. Если коэффициент корреляции значимо отличается от нуля, то это может указывать на то, что между переменными существует какая-то взаимосвязь.

   Наконец, мы проанализируем значение непараметрической оценки плотности переменной X в точке 55. Это позволит нам оценить, насколько часто встречаются значения переменной X в окрестности этой точки. Если значение оценки плотности велико, то это указывает на то, что в окрестности точки 55 находится много наблюдений. Если значение оценки плотности мало, то это указывает на то, что в окрестности точки 55 находится мало наблюдений.

   Важно отметить, что непараметрическая оценка плотности является только оценкой, и она может быть неточной, особенно если размер выборки мал. Поэтому необходимо использовать другие методы анализа, чтобы подтвердить или опровергнуть результаты, полученные с помощью непараметрической оценки плотности.

   После того, как все результаты были проанализированы, мы можем сделать некоторые выводы о структуре данных и взаимосвязях между переменными. Эти выводы могут быть использованы для дальнейших исследований или для принятия управленческих решений.

   В заключение, необходимо отметить, что непараметрические методы являются мощным инструментом для анализа данных, который позволяет исследователям избегать жестких предположений о форме распределений и функциональных зависимостях. Однако, использование непараметрических методов требует осторожности и внимания к деталям. Необходимо тщательно выбирать параметры методов и интерпретировать полученные результаты с учетом ограничений этих методов.

   Таким образом, сгенерированные данные, отражают определенные характеристики, которые необходимо учитывать при анализе.

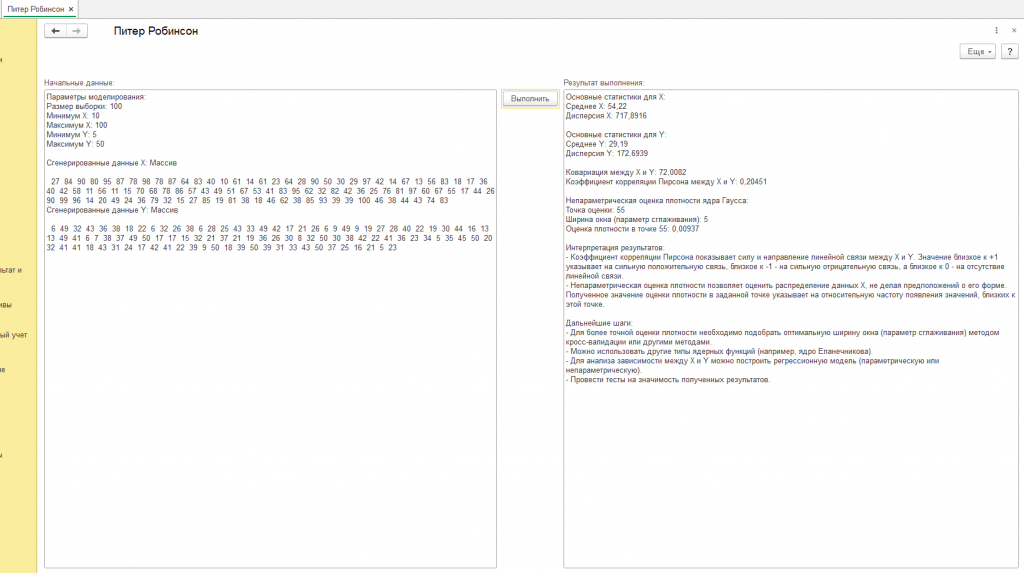
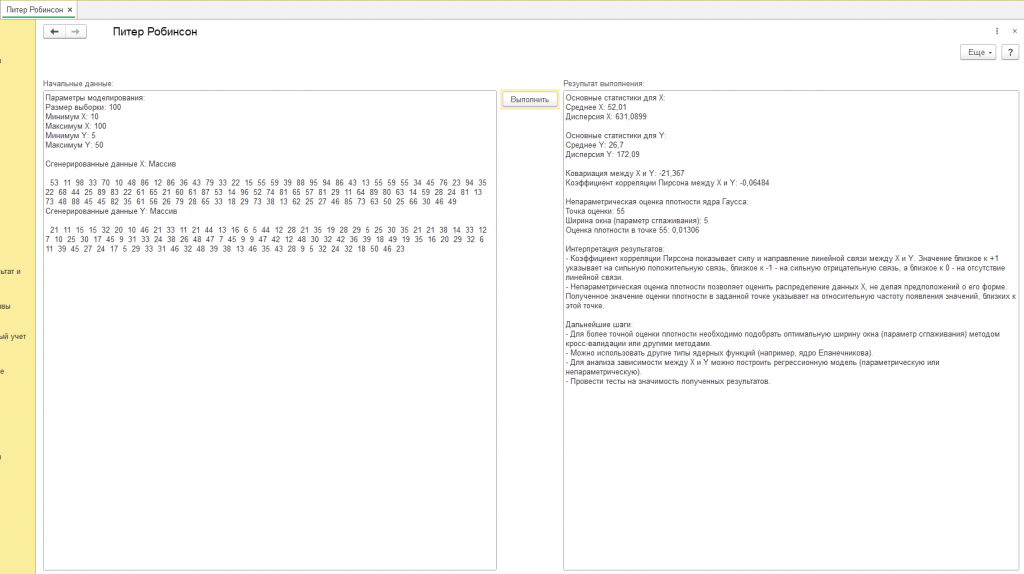
   Сгенерированные данные X: Массив 13 23 19 52 32 48 39 61 99 44 49 14 32 57 65 53 98 85 72 64 48 30 97 55 89 13 96 56 20 25 22 18 30 31 55 25 11 82 50 71 56 19 98 38 94 100 24 68 35 46 88 14 48 24 81 25 78 44 51 42 52 74 55 39 18 54 82 100 69 51 59 43 39 54 12 16 83 87 11 43 57 21 54 90 34 72 71 10 39 81 17 44 78 63 85 64 23 31 12 79

   Сгенерированные данные Y: Массив 33 47 15 5 48 10 29 47 50 28 39 35 43 29 23 48 46 16 43 22 49 11 45 11 31 21 48 5 34 42 43 40 24 22 41 28 32 23 30 10 39 41 35 40 27 12 30 30 22 23 39 42 5 30 45 10 9 17 24 10 39 11 8 37 44 11 8 41 20 30 47 49 13 36 13 15 26 45 33 16 6 29 28 10 35 6 21 23 49 29 26 28 19 39 27 10 50 29 21 7

   Статистические характеристики рассчитанные на их основе, позволяют сделать предварительные выводы о природе переменных.

*Основные статистики для X: Среднее X: 50,82 Дисперсия X: 683,2876

Основные статистики для Y: Среднее Y: 28,1 Дисперсия Y: 181,67

Ковариация между X и Y: -17,352 Коэффициент корреляции Пирсона между X и Y: -0,04925

Непараметрическая оценка плотности ядра Гаусса: Точка оценки: 55 Ширина окна (параметр сглаживания): 5 Оценка плотности в точке 55: 0,01496*

   В частности, отсутствие значимой линейной связи между переменными указывает на необходимость применения более сложных методов анализа, способных выявлять нелинейные зависимости.

   Оценка плотности переменной X в точке 55 позволяет получить представление о концентрации значений в окрестности этой точки.

    Дальнейшие исследования могут быть направлены на уточнение оценки плотности с использованием различных методов выбора ширины окна, а также на выявление нелинейных зависимостей между переменными с помощью других непараметрических методов.

   Несомненно, работы Питера Робинсона оказали значительное влияние на развитие эконометрики и стимулировали активное использование непараметрических методов в анализе данных. Его идеи продолжают вдохновлять исследователей на поиск новых подходов к моделированию экономических явлений и на более глубокое понимание сложных взаимосвязей между переменными. В данном анализе мы коснулись лишь одного аспекта его обширного вклада, однако надеемся, что это позволит читателю оценить важность и перспективность непараметрических методов в эконометрике.

   Продолжение данного исследования, в контексте работ Питера Робинсона, может включать в себя анализ полупараметрических моделей, которые позволяют сочетать преимущества параметрических и непараметрических подходов. Такие модели могут быть особенно полезны в ситуациях, когда некоторые аспекты структуры данных известны, а другие – требуют непараметрической оценки. Также, представляет интерес изучение методов робастной эконометрики, которые позволяют получать надежные оценки даже в условиях наличия выбросов и других аномалий в данных. Эти направления исследований являются важными для развития эконометрики и позволяют решать широкий круг практических задач.

   Сделанные выводы, подчеркивают важность непараметрических методов для анализа экономических данных, особенно в ситуациях, когда предположения о линейности и нормальности распределения не выполняются.

   Использование непараметрических методов позволяет исследователям получать более точные и надежные результаты, что, в конечном итоге, способствует лучшему пониманию экономических явлений и принятию более обоснованных управленческих решений.

    Важно отметить, что непараметрические методы не являются панацеей и имеют свои ограничения. В частности, они могут требовать больших объемов данных и быть более вычислительно сложными, чем параметрические методы. Поэтому, выбор между параметрическими и непараметрическими методами должен основываться на тщательном анализе конкретной исследовательской задачи и доступных данных.

   Тем не менее, непараметрические методы представляют собой важный инструмент в арсенале эконометриста и позволяют решать широкий круг задач, которые не могут быть решены с помощью традиционных параметрических подходов. Работы Питера Робинсона сыграли ключевую роль в популяризации и развитии этих методов, и его вклад в эконометрику трудно переоценить.

   В заключение, хотелось бы отметить, что эконометрика продолжает развиваться, и новые методы анализа данных появляются постоянно. Однако, основные принципы, заложенные Питером Робинсоном, остаются актуальными и продолжают вдохновлять исследователей на поиск новых подходов к моделированию экономических явлений. Данный анализ, хоть и является простым, демонстрирует ценность непараметрических методов и служит отправной точкой для более глубоких исследований в этой области. 

Развитие идей Питера Робинсона: полупараметрический подход и анализ временных рядов

     Следует подчеркнуть, что вклад Питера Робинсона в эконометрику выходит далеко за рамки простых непараметрических методов. Его работы охватывают широкий спектр теоретических и прикладных вопросов, включая полупараметрические модели, анализ временных рядов и робастные методы оценивания. Эти направления исследований демонстрируют глубину его понимания эконометрических проблем и его стремление к созданию более надежных и эффективных инструментов для анализа экономических данных.

     Одной из наиболее значительных областей, в которой Робинсон внес существенный вклад, является разработка и применение полупараметрических моделей. Эти модели представляют собой компромисс между параметрическими и непараметрическими подходами. Они позволяют объединить преимущества обоих подходов, используя параметрические методы для моделирования тех аспектов данных, о которых у исследователя имеются определенные знания, и непараметрические методы для моделирования тех аспектов, о которых знаний недостаточно.

     В полупараметрических моделях некоторые параметры оцениваются с помощью традиционных параметрических методов, таких как метод наименьших квадратов или метод максимального правдоподобия. Остальные параметры оцениваются с использованием непараметрических методов, таких как оценка плотности ядра или сглаживание. Такой подход позволяет исследователю получать более точные и надежные оценки параметров модели, чем при использовании только параметрических или только непараметрических методов.

     В качестве примера полупараметрической модели можно привести частично линейную модель. В этой модели предполагается, что зависимая переменная является линейной функцией от некоторых объясняющих переменных и нелинейной функцией от других объясняющих переменных. Линейная часть модели оценивается с помощью традиционных параметрических методов, а нелинейная часть оценивается с помощью непараметрических методов, таких как сглаживание или оценка плотности ядра. Такой подход позволяет исследователю учитывать нелинейные зависимости между переменными, которые не могут быть учтены с помощью традиционных линейных моделей.

     Полупараметрические модели особенно полезны в ситуациях, когда исследователь имеет ограниченные знания о функциональной форме зависимости между переменными. В этом случае, использование полупараметрических моделей позволяет исследователю избежать жестких предположений о функциональной форме зависимости и получить более точные и надежные оценки параметров модели.

     Другим важным направлением исследований Питера Робинсона является анализ временных рядов. Временные ряды представляют собой последовательности наблюдений, упорядоченных во времени. Анализ временных рядов является важным инструментом для изучения экономических процессов, таких как инфляция, безработица, экономический рост и финансовые рынки.

     Питер Робинсон внес значительный вклад в разработку методов анализа временных рядов, в частности, методов анализа долгосрочной памяти (long memory). Долгосрочная память относится к ситуации, когда значения временного ряда в разные моменты времени сильно зависят друг от друга, даже если эти моменты времени разделены большим промежутком времени. Анализ долгосрочной памяти является важным инструментом для изучения экономических процессов, таких как финансовые рынки, где долгосрочная память может быть вызвана информационными каскадами или инерцией инвесторов.

     Методы анализа долгосрочной памяти, разработанные Робинсоном, позволяют исследователям оценивать степень долгосрочной памяти в данных и использовать эту информацию для прогнозирования будущих значений временного ряда. Эти методы основаны на использовании дробных интегральных процессов, которые позволяют моделировать долгосрочную зависимость между значениями временного ряда.

     Робинсон также внес вклад в разработку методов анализа стационарных и нестационарных временных рядов. Стационарный временной ряд характеризуется постоянными статистическими свойствами во времени, в то время как нестационарный временной ряд характеризуется изменяющимися статистическими свойствами во времени. Анализ нестационарных временных рядов является важным инструментом для изучения экономических процессов, таких как экономический рост, который может быть нестационарным из-за технологических изменений и других факторов.

     Робинсон разработал методы анализа как стационарных, так и нестационарных временных рядов, которые позволяют исследователям оценивать параметры моделей и делать прогнозы. Его методы основаны на использовании различных инструментов, таких как преобразование Фурье, спектральный анализ и методы оценивания параметров моделей.

     Помимо полупараметрических моделей и анализа временных рядов, Питер Робинсон внес значительный вклад в развитие робастных методов оценивания. Робастные методы оценивания предназначены для получения надежных оценок параметров моделей даже в условиях наличия выбросов и других аномалий в данных. Выбросы – это наблюдения, которые значительно отличаются от остальных наблюдений в выборке. Выбросы могут быть вызваны различными факторами, такими как ошибки измерения, ошибки ввода данных или экстремальные события.

     Традиционные методы оценивания, такие как метод наименьших квадратов, чувствительны к выбросам. Выбросы могут оказывать значительное влияние на оценки параметров модели и приводить к искаженным результатам. Робастные методы оценивания разработаны для того, чтобы уменьшить влияние выбросов на оценки параметров модели и получить более надежные результаты.

     Робастные методы оценивания основаны на использовании различных подходов, таких как использование альтернативных функций потерь, которые менее чувствительны к выбросам, или использование процедур взвешивания, которые уменьшают вклад выбросов в оценки параметров модели. Эти методы позволяют исследователям получать более точные и надежные оценки параметров моделей даже в условиях наличия выбросов в данных.

     В заключение, вклад Питера Робинсона в эконометрику огромен и многогранен. Его работы в области полупараметрических моделей, анализа временных рядов и робастных методов оценивания оказали значительное влияние на развитие эконометрики и стимулировали активное использование непараметрических методов в анализе данных. Его идеи продолжают вдохновлять исследователей на поиск новых подходов к моделированию экономических явлений и на более глубокое понимание сложных взаимосвязей между переменными.

     Полупараметрические методы, разработанные Робинсоном, открывают новые горизонты в анализе данных, позволяя исследователям избежать жестких предположений о форме распределений и функциональных зависимостях. Анализ временных рядов с использованием методов долгосрочной памяти позволяет исследователям лучше понимать динамику экономических процессов и делать более точные прогнозы. Робастные методы оценивания позволяют получать надежные оценки параметров моделей даже в условиях наличия выбросов и других аномалий в данных.

     Важно отметить, что работы Робинсона являются не только теоретическими, но и имеют важное практическое значение. Его методы широко используются в различных областях экономики, таких как финансы, макроэкономика, микроэкономика и экономика окружающей среды. Применение его методов позволяет исследователям получать более точные и надежные результаты, что, в конечном итоге, способствует лучшему пониманию экономических явлений и принятию более обоснованных управленческих решений.

     Работы Питера Робинсона также оказали значительное влияние на развитие эконометрических программных пакетов, таких как R и Stata. Его методы были реализованы в этих пакетах, что сделало их доступными для широкого круга исследователей.

     Нельзя не отметить, что работы Робинсона, касающиеся анализа временных рядов, особенно актуальны в современном мире, где объем доступных данных о финансовых рынках постоянно растет. Методы, разработанные Робинсоном, позволяют анализировать сложные динамические процессы и делать прогнозы на основе этих данных.

     В заключение, вклад Питера Робинсона в эконометрику является выдающимся. Его работы в области непараметрических и полупараметрических методов, анализа временных рядов и робастных методов оценивания оказали значительное влияние на развитие эконометрики и стимулировали активное использование этих методов в различных областях экономики. Его идеи продолжают вдохновлять исследователей на поиск новых подходов к моделированию экономических явлений и на более глубокое понимание сложных взаимосвязей между переменными. Его наследие будет продолжать жить в работах других исследователей и в практике экономических исследований на протяжении многих лет.