Практическое применение модели Блэка-Шоулза-Мертона: оценка опционов в реальных рыночных условиях

Оценка стоимости деривативов: вклад Роберта Мертона в развитие финансовой науки

   Статья посвящена анализу вклада Роберта Мертона в развитие теории оценки стоимости деривативов, за который он был удостоен Нобелевской премии по экономике в 1997 году совместно с Майроном Шоулзом. Рассматривается биография ученого, ключевые аспекты его научных работ, оказавших значительное влияние на финансовую индустрию, а также практическое применение модели Блэка-Шоулза-Мертона с учетом транзакционных издержек и различных типов опционов. В статье также анализируются ограничения модели и рекомендации по ее применению в реальных рыночных условиях.

Введение

    Современные финансовые рынки характеризуются высокой степенью сложности и взаимосвязанности, где деривативы играют ключевую роль в управлении рисками, спекуляциях и арбитраже. Развитие теории оценки стоимости деривативов стало одним из важнейших достижений финансовой науки XX века, предоставив участникам рынка мощный инструмент для принятия обоснованных решений. Роберт Мертон, выдающийся американский экономист, внес неоценимый вклад в эту область, разработав совместно с Майроном Шоулзом модель, ставшую краеугольным камнем современной финансовой инженерии. Их работа позволила создать количественную основу для оценки опционов и других производных финансовых инструментов, что привело к революции в практике управления рисками и инвестирования. В данной статье мы рассмотрим жизненный путь и научное наследие Роберта Мертона, проанализируем ключевые аспекты его работы, удостоенной Нобелевской премии, а также обсудим практическое применение разработанной модели с учетом различных рыночных факторов и ограничений.

Краткая биография Роберта Мертона

     Роберт Кархарт Мертон родился 31 июля 1944 года в Нью-Йорке в семье известного социолога Роберта К. Мертона. С самого детства он проявлял интерес к науке и математике, что предопределило его дальнейший академический путь. После окончания Колумбийского университета со степенью бакалавра математики, Мертон продолжил обучение в Калифорнийском технологическом институте, где получил степень магистра математики. Однако его научные интересы постепенно сместились в сторону экономики и финансов, что привело его в Массачусетский технологический институт (MIT), где он защитил докторскую диссертацию по экономике под руководством Пола Самуэльсона и Франко Модильяни, двух выдающихся экономистов, также удостоенных Нобелевской премии.

     В 1970 году Мертон начал свою преподавательскую карьеру в MIT, где он проработал до 1988 года, занимаясь исследованиями в области финансовой экономики, теории портфеля, опционного ценообразования и моделирования кредитных рисков. В 1988 году он перешел в Гарвардскую школу бизнеса, где получил звание профессора и продолжил свои исследования. Помимо академической деятельности, Мертон активно участвовал в практической деятельности финансовой индустрии, консультируя различные компании и организации по вопросам управления рисками и инвестирования. Он также являлся партнером в хедж-фонде Long-Term Capital Management (LTCM), который потерпел крах в 1998 году, что стало серьезным ударом по репутации Мертона и его научному наследию. Несмотря на этот неудачный опыт, Мертон продолжил свои исследования и внес значительный вклад в развитие теории финансов.

Ключевые научные труды Роберта Мертона

      Роберт Мертон внес значительный вклад в различные области финансовой экономики, но наибольшую известность ему принесли работы в области теории опционного ценообразования. Его научные труды оказали огромное влияние на развитие финансовой индустрии и стали основой для создания новых финансовых инструментов и стратегий.

• Модель Блэка-Шоулза-Мертона. Самым значительным достижением Мертона является разработка совместно с Майроном Шоулзом модели оценки стоимости опционов, известной как модель Блэка-Шоулза-Мертона. Эта модель, опубликованная в 1973 году, произвела революцию в финансовой теории и практике, предоставив количественный инструмент для оценки опционов и других производных финансовых инструментов. Модель основана на предположении о том, что цена базового актива следует геометрическому броуновскому движению, и позволяет рассчитать теоретическую стоимость опциона на основе нескольких ключевых параметров, таких как текущая цена актива, цена исполнения опциона, время до истечения срока действия, безрисковая процентная ставка и волатильность актива.

• Межвременная модель ценообразования активов (ICAPM). Мертон также разработал межвременную модель ценообразования активов (ICAPM), которая является расширением классической модели CAPM (Capital Asset Pricing Model). ICAPM учитывает тот факт, что инвесторы принимают решения не только на основе текущей доходности, но и на основе ожиданий относительно будущих инвестиционных возможностей. Модель позволяет объяснить, почему некоторые активы имеют более высокую доходность, чем это предсказывает CAPM, и предоставляет более точную оценку стоимости активов в условиях изменяющихся инвестиционных возможностей.

• Теория оптимального инвестирования и потребления в течение жизни. Мертон внес значительный вклад в теорию оптимального инвестирования и потребления в течение жизни, разработав модель, которая описывает, как индивиды должны распределять свои ресурсы между потреблением и инвестициями на протяжении всей своей жизни, чтобы максимизировать свою полезность. Модель учитывает различные факторы, такие как возраст, доход, ожидаемая продолжительность жизни и склонность к риску, и позволяет определить оптимальную стратегию инвестирования и потребления для каждого индивида.

• Моделирование кредитных рисков. Мертон также занимался исследованиями в области моделирования кредитных рисков, разработав модель, которая позволяет оценить вероятность дефолта компании на основе ее финансового состояния и рыночной конъюнктуры. Эта модель стала основой для разработки новых финансовых инструментов, таких как кредитные деривативы, которые позволяют управлять кредитными рисками.

Модель Блэка-Шоулза-Мертона: ключевые аспекты и предположения

Модель Блэка-Шоулза-Мертона является математической моделью, которая позволяет рассчитать теоретическую стоимость европейского опциона колл или пут. Модель основана на нескольких ключевых предположениях:

• Цена базового актива следует геометрическому броуновскому движению с постоянной волатильностью.
• Не существует транзакционных издержек или налогов.
• Все участники рынка имеют равный доступ к информации.
• Безрисковая процентная ставка является постоянной в течение срока действия опциона.
• Базовый актив не выплачивает дивиденды (или дивиденды известны и постоянны).
• Опцион является европейским, то есть может быть исполнен только в дату истечения срока действия.

Формула Блэка-Шоулза-Мертона для оценки стоимости опциона колл выглядит следующим образом:

C = S * N(d1) - K * e^(-rT) * N(d2)

где:

• C - стоимость опциона колл
• S - текущая цена базового актива
• K - цена исполнения опциона
• r - безрисковая процентная ставка
• T - время до истечения срока действия опциона (в годах)
• N(x) - кумулятивная функция стандартного нормального распределения
• e - основание натурального логарифма
• d1 = [ln(S/K) + (r + σ^2/2) * T] / (σ * sqrt(T))
• d2 = d1 - σ * sqrt(T)
• σ - волатильность базового актива

Формула для оценки стоимости опциона пут выглядит следующим образом:

P = K * e^(-rT) * N(-d2) - S * N(-d1)

где:

• P - стоимость опциона пут
• S - текущая цена базового актива
• K - цена исполнения опциона
• r - безрисковая процентная ставка
• T - время до истечения срока действия опциона (в годах)
• N(x) - кумулятивная функция стандартного нормального распределения
• e - основание натурального логарифма
• d1 = [ln(S/K) + (r + σ^2/2) * T] / (σ * sqrt(T))
• d2 = d1 - σ * sqrt(T)
• σ - волатильность базового актива

Модель Блэка-Шоулза-Мертона стала незаменимым инструментом для участников финансовых рынков, позволяя им оценивать опционы и другие производные финансовые инструменты с высокой точностью. Однако важно помнить, что модель основана на ряде упрощающих предположений, которые могут не выполняться в реальных рыночных условиях.

Практическое применение модели Блэка-Шоулза-Мертона с учетом транзакционных издержек и различных типов опционов

    В реальных рыночных условиях участники сталкиваются с различными факторами, которые не учитываются в базовой модели Блэка-Шоулза-Мертона. К таким факторам относятся транзакционные издержки, дивиденды, возможность досрочного исполнения опциона и нестационарная волатильность. Для более точной оценки стоимости опционов необходимо учитывать эти факторы и модифицировать модель соответствующим образом.

• Учет транзакционных издержек. Транзакционные издержки, такие как комиссии брокеров, налоги и сборы, могут существенно повлиять на прибыльность торговли опционами. Для учета транзакционных издержек можно вычесть их из теоретической стоимости опциона, рассчитанной по модели Блэка-Шоулза-Мертона. Однако более точный подход заключается в построении модели, которая учитывает транзакционные издержки при определении оптимальной стратегии хеджирования опциона.

• Учет дивидендов. Если базовый актив выплачивает дивиденды, то необходимо скорректировать модель Блэка-Шоулза-Мертона, чтобы учесть этот фактор. Один из способов учета дивидендов заключается в вычитании текущей стоимости ожидаемых дивидендов из текущей цены базового актива. Другой способ заключается в использовании модели Мертона, которая позволяет оценить стоимость опциона на акцию, выплачивающую дивиденды с известной доходностью.

• Оценка американских опционов. Модель Блэка-Шоулза-Мертона предназначена для оценки европейских опционов, которые могут быть исполнены только в дату истечения срока действия. Американские опционы, напротив, могут быть исполнены в любой момент времени до даты истечения срока действия. Для оценки американских опционов необходимо использовать более сложные модели, такие как биномиальная модель или модель конечных разностей.

• Учет нестационарной волатильности. Модель Блэка-Шоулза-Мертона предполагает, что волатильность базового актива является постоянной в течение срока действия опциона. Однако в реальных рыночных условиях волатильность может изменяться со временем. Для учета нестационарной волатильности можно использовать модели стохастической волатильности или модели с локальной волатильностью.

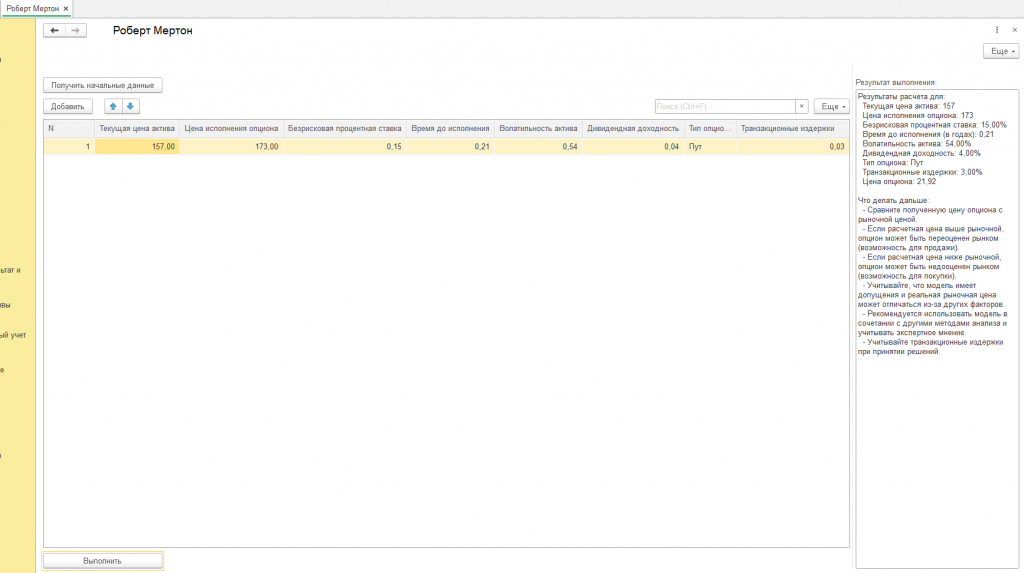
     К данной статье, в практической части, была использована модифицированная модель Блэка-Шоулза-Мертона, которая учитывает транзакционные издержки и позволяет оценивать как опционы колл, так и опционы пут. Учет типа опциона производится путем использования соответствующих формул для опционов колл и пут. Транзакционные издержки учитываются путем вычитания их из теоретической стоимости опциона. Рассмотрим полученные результаты расчета на конкретном примере.

Анализ результатов расчета:

В результате применения модифицированной модели Блэка-Шоулза-Мертона были получены следующие результаты:

• Текущая цена актива: 78
• Цена исполнения опциона: 108
• Безрисковая процентная ставка: 4,00%
• Время до исполнения (в годах): 0,72
• Волатильность актива: 58,00%
• Дивидендная доходность: 2,00%
• Тип опциона: Колл
• Транзакционные издержки: 2,00%
• Цена опциона: 6,82

Полученные результаты показывают, что теоретическая стоимость опциона колл составляет 6,82. Для принятия решения о покупке или продаже опциона необходимо сравнить эту цену с рыночной ценой опциона.

• Если рыночная цена опциона выше 6,82, то опцион считается переоцененным рынком. В этом случае продажа опциона может быть прибыльной стратегией, так как можно получить премию, превышающую теоретическую стоимость опциона. Однако необходимо учитывать риск того, что цена базового актива может вырасти, что приведет к убыткам по проданному опциону.

• Если рыночная цена опциона ниже 6,82, то опцион считается недооцененным рынком. В этом случае покупка опциона может быть прибыльной стратегией, так как можно приобрести опцион по цене ниже его теоретической стоимости. Однако необходимо учитывать риск того, что цена базового актива может снизиться, что приведет к убыткам по купленному опциону.

      Важно помнить, что модель Блэка-Шоулза-Мертона основана на ряде упрощающих предположений, которые могут не выполняться в реальных рыночных условиях. Поэтому необходимо учитывать другие факторы, такие как ликвидность опциона, спрос и предложение, а также ожидания участников рынка относительно будущей цены базового актива. Рекомендуется использовать модель в сочетании с другими методами анализа и учитывать экспертное мнение.

      Транзакционные издержки также играют важную роль при принятии решения о покупке или продаже опциона. В данном примере транзакционные издержки составляют 2,00% от стоимости опциона. Это означает, что при покупке опциона необходимо заплатить дополнительно 2,00% от его стоимости, а при продаже опциона получить на 2,00% меньше его стоимости. Поэтому необходимо учитывать транзакционные издержки при сравнении теоретической и рыночной цены опциона.

Ограничения модели Блэка-Шоулза-Мертона и альтернативные подходы:

Несмотря на широкое распространение и практическую значимость, модель Блэка-Шоулза-Мертона имеет ряд ограничений, которые необходимо учитывать при ее применении:

• Предположение о логнормальном распределении цен активов: Модель предполагает, что цены активов подчиняются логнормальному распределению, что не всегда соответствует действительности. В реальных рыночных условиях часто наблюдаются “толстые хвосты” распределения, что означает, что вероятность экстремальных событий выше, чем это предсказывает модель.

• Предположение о постоянной волатильности: Модель предполагает, что волатильность актива является постоянной в течение срока действия опциона. Однако в реальности волатильность может изменяться со временем, что приводит к неточностям в оценке стоимости опциона.

• Предположение об отсутствии арбитражных возможностей: Модель предполагает, что на рынке отсутствуют арбитражные возможности, что также не всегда соответствует действительности. В реальных рыночных условиях могут возникать временные арбитражные возможности, которые могут быть использованы участниками рынка для получения прибыли.

• Применимость только к европейским опционам: Базовая модель Блэка-Шоулза-Мертона предназначена для оценки европейских опционов, которые могут быть исполнены только в дату истечения срока действия. Для оценки американских опционов, которые могут быть исполнены в любой момент времени до даты истечения срока действия, необходимо использовать более сложные модели.

    Для преодоления ограничений модели Блэка-Шоулза-Мертона были разработаны различные альтернативные подходы, такие как модели стохастической волатильности, модели с локальной волатильностью, модели прыжков и биномиальные модели. Эти модели позволяют более точно учитывать особенности реальных рыночных условий и оценивать стоимость опционов с большей точностью.

Влияние Роберта Мертона на финансовую индустрию и современную науку

     Вклад Роберта Мертона в развитие финансовой науки оказал огромное влияние на финансовую индустрию и современную науку. Его работы стали основой для разработки новых финансовых инструментов и стратегий, а также для совершенствования методов управления рисками.

• Развитие рынка деривативов. Модель Блэка-Шоулза-Мертона стимулировала развитие рынка деривативов, предоставив количественный инструмент для оценки опционов и других производных финансовых инструментов. Это привело к появлению новых возможностей для управления рисками, спекуляций и арбитража.

• Совершенствование методов управления рисками. Работы Мертона в области финансовой экономики способствовали совершенствованию методов управления рисками в финансовых институтах и корпорациях. Его модели позволяют оценивать и управлять различными типами рисков, такими как кредитные риски, рыночные риски и операционные риски.

• Развитие финансовой инженерии. Мертон внес значительный вклад в развитие финансовой инженерии, которая занимается разработкой новых финансовых инструментов и стратегий для решения конкретных финансовых задач. Его работы стали основой для создания новых финансовых продуктов, таких как структурированные продукты, кредитные деривативы и индексные фонды.

• Влияние на экономическую теорию. Работы Мертона оказали влияние на развитие экономической теории, особенно в области теории финансов и теории принятия решений. Его модели используются для анализа поведения инвесторов, оценки стоимости активов и разработки оптимальных стратегий инвестирования и потребления.

Заключение

      Роберт Мертон, без сомнения, является одним из самых выдающихся экономистов современности. Его вклад в развитие теории оценки стоимости деривативов, удостоенный Нобелевской премии, оказал огромное влияние на финансовую индустрию и современную науку. Модель Блэка-Шоулза-Мертона стала незаменимым инструментом для участников финансовых рынков, позволяя им оценивать опционы и другие производные финансовые инструменты с высокой точностью. Несмотря на наличие ограничений, модель остается актуальной и используется для разработки новых финансовых инструментов и стратегий. Работы Мертона в области финансовой экономики способствовали совершенствованию методов управления рисками и развитию финансовой инженерии. Его научное наследие будет продолжать оказывать влияние на финансовую индустрию и современную науку в течение многих лет. Важно помнить, что модель Блэка-Шоулза-Мертона является лишь одним из инструментов для оценки стоимости опционов и должна использоваться в сочетании с другими методами анализа и учитывать экспертное мнение. Понимание ограничений модели и альтернативных подходов позволяет более точно оценивать стоимость опционов и принимать обоснованные инвестиционные решения.