Меня зовут Александр, я программист Python, C#, PHP, 1C в компании Programming Store, а также действующий преподаватель (доцент) ИЖГТУ им. М. Т. Калашникова, кандидат технических наук, читаю курс «Технологии и методы программирования».
Меня зовут Александр, я программист Python, C#, PHP, 1C в компании Programming Store, а также действующий преподаватель (доцент) ИЖГТУ им. М. Т. Калашникова, кандидат технических наук, читаю курс «Технологии и методы программирования».
В данной статье я хотел бы поделиться процессом построения алгоритмов и принципами работы с ними.
Содержание
1. Зачем нужна теория алгоритмов.
2. Процесс построение алгоритма.
3. Массивы. Алгоритмы для работы с массивами.
4. Списки. Алгоритмы для работы со списками
5. Деревья. Алгоритмы работы с деревьями.
6. Хэш-таблица
7. Типизированные файлы (бинарные файлы)
8. Резюме
Зачем нужна теория алгоритмов
Представьте, что вы написали программу, которая отлично работает на небольшом наборе данных. Но что произойдет, если количество данных увеличится в разы или даже на порядки? Скорость работы может упасть, программа начнет «тормозить», а иногда и вовсе зависнет. Именно здесь на помощь приходит анализ алгоритмов.
Кстати, сразу замечу, что если размер набора данных возрастет в два раза, то не факт, что время выполнения программы тоже возрастет в два раза. Эта зависимость может быть не линейной. Например, в случае алгоритма пузырьковой сортировки, время работы увеличится в четыре раза
Таким образом, теория алгоритмов – фундамент эффективного программирования. Понимание алгоритмов позволит вам писать быстрый и надежный код, решать сложные задачи и оптимизировать производительность ваших проектов. В этой статье мы рассмотрим основные алгоритмические структуры данных, такие как массивы, списки, деревья и хэш-таблицы, а также методы их обработки, чтобы вы могли применять эти знания на практике.
Процесс построение алгоритма
Алгоритм – это четкая и конечная последовательность инструкций, направленная на решение определенной задачи. Построение алгоритма – творческий процесс, который обычно включает следующие этапы:
1. Постановка задачи.
Четкое определение проблемы, которую нужно решить. Определение входных данных и ожидаемого результата.
2. Построение модели.
Создание абстрактного представления задачи. Определение сущностей, связей между ними и операций, которые необходимо выполнить. Модель может быть математической, логической или графической. В зависимости от задачи это может быть:
• математическая модель: уравнения, формулы, описывающие поведение системы;
• логическая модель: правила, логические выражения, определяющие условия;
• графическая модель: диаграммы, блок-схемы, отображающие процессы.
3. Разработка алгоритма.
Определение шагов, необходимых для решения задачи на основе построенной модели. Использование блок-схем, псевдокода или языка программирования.
4. Реализация алгоритма.
Перевод алгоритма в код на выбранном языке программирования.
5. Тестирование и отладка.
Проверка правильности работы алгоритма на различных входных данных и исправление ошибок.
6. Анализ алгоритма.
Оценка эффективности алгоритма по времени выполнения и объему используемой памяти.
Построение модели — критический этап. Плохо построенная модель приведет к неэффективному или даже неправильному алгоритму. Примером может служить задача маршрутизации: моделью может быть граф, где города — вершины, а дороги — ребра с весами (расстояние, время).
Массивы. Алгоритмы для работы с массивами
Массив – это структура данных, представляющая собой последовательность элементов одного типа, хранящихся в смежных ячейках памяти.
Характерные алгоритмы для массивов — это, конечно же, поиск элемента. Если массив не сортирован, то поиск идет обычным перебором и сравнением. Если массив отсортирован, то можно применить бинарный поиск, который работает значительно быстрее. Также типичной операцией является поиск в массиве минимума и максимума, вычисление его суммы, среднего арифметического либо иной агрегатной функции, инвертирование массива и поиск дубликатов.
Разберем некоторые из этих алгоритмов подробнее.
Линейный поиск. Это последовательный перебор элементов массива до нахождения искомого элемента. Простой, но неэффективный для больших массивов. В C# такой алгоритм реализует метод массива IndexOf().
Бинарный поиск. Работает только для отсортированных массивов. Делит массив пополам и сравнивает средний элемент с искомым. Эффективен для больших массивов (логарифмическая сложность). В C# этот алгоритм реализован в методе BinarySearch().
Отличие линейного и бинарного поиска можно проиллюстрировать следующими картинками.
Вот линейный поиск, он перебирает все элементы, пока не найдёт искомый или пока не кончится список (массив):
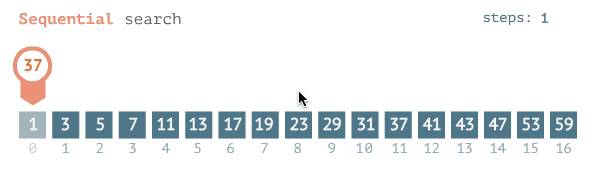
А вот бинарный поиск, он на каждой итерации делит список (массив) на две части, каждый раз сужая область поиска, за счет чего количество итераций сильно уменьшается и алгоритм работает очень быстро:
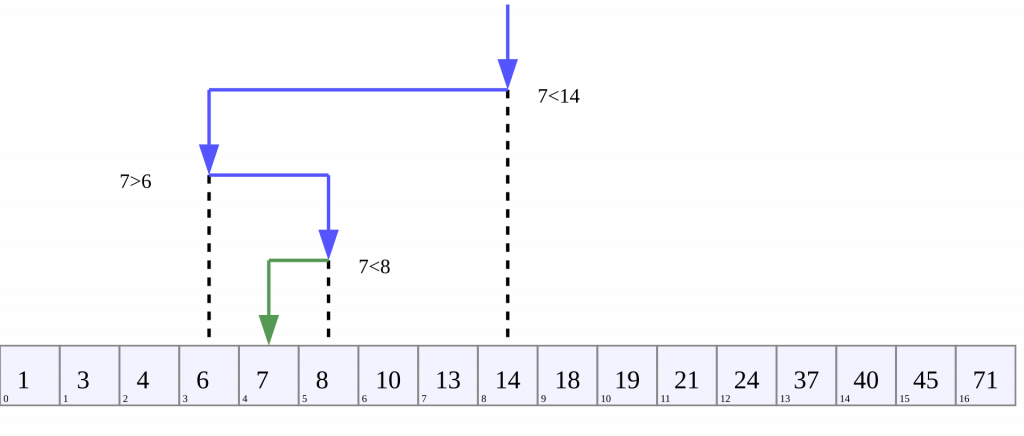
Теперь поговорим о сортировке массивов.
Пузырьковая сортировка. Сравнивает соседние элементы и меняет их местами, если они расположены в неправильном порядке. Простой в реализации, но неэффективный для больших массивов.
Работу этого алгоритма иллюстрирует такая картинка:
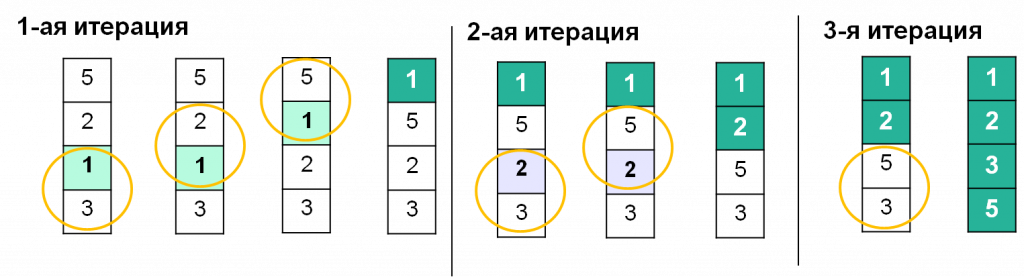
Быстрая сортировка (Quicksort). Выбирает опорный элемент и разделяет массив на две части: элементы меньше опорного и элементы больше опорного. Рекурсивно сортирует каждую часть. Эффективна для большинства случаев.
Этот алгоритм иллюстрирует следующая картинка:
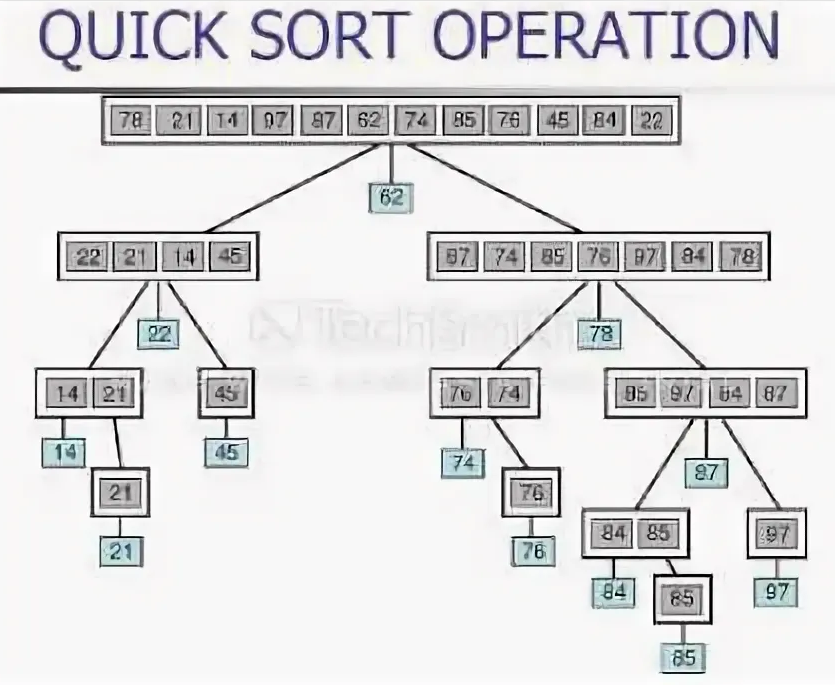
Во многих языках программирования есть встроенная функция быстрой сортировки:
• C#: Array.Sort() (использует различные алгоритмы сортировки, включая Quicksort)
• Python: sorted() (возвращает новый отсортированный список), list.sort() (сортирует список на месте)
Пример реализации (C#):
int[] numbers = { 5, 2, 8, 1, 9 };
Array.Sort(numbers); // Сортировка массива по возрастанию
Console.WriteLine(string.Join(", ", numbers)); // Вывод: 1, 2, 5, 8, 9
Пример реализации (Python):
numbers = [5, 2, 8, 1, 9]
numbers.sort() # Сортировка списка на месте
print(numbers) # Вывод: [1, 2, 5, 8, 9]
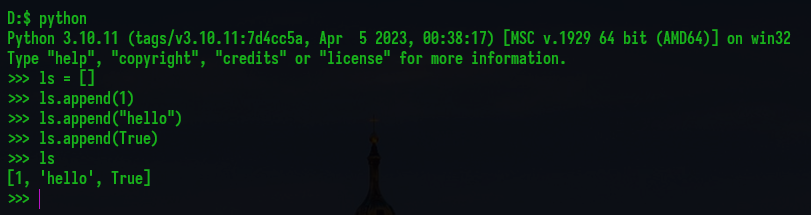
Списки. Алгоритмы для работы со списками
Список (List) – это динамическая структура данных, позволяющая хранить упорядоченную последовательность элементов. В отличие от массивов размер списка может изменяться во время выполнения программы.
Алгоритмы для работы со списками:
• Добавление элемента:
* В конец списка (Append/Add).
* В начало списка (Insert).
* В произвольную позицию (Insert).
• Удаление элемента:
* По значению (Remove/RemoveAt).
* По индексу (RemoveAt).
• Поиск элемента: Линейный поиск (аналогичен массивам).
• Сортировка списка: Аналогично массивам.
• Другие алгоритмы:
* Инвертирование списка.
* Объединение списков.
* Разделение списка.
C#: List<T>
Python: list
Пример реализации (C#):
R03;R03;R03;R03;R03;R03;R03;List<string> names = new List<string>() { "Alice", "Bob", "Charlie" };
names.Add("David"); // Добавление в конец
names.Insert(0, "Eve"); // Добавление в начало
Console.WriteLine(string.Join(", ", names)); // Вывод: Eve, Alice, Bob, Charlie, David
Пример реализации (Python):
names = ["Alice", "Bob", "Charlie"]
names.append("David") # Добавление в конец
names.insert(0, "Eve") # Добавление в начало
print(names) # Вывод: ['Eve', 'Alice', 'Bob', 'Charlie', 'David']
Деревья. Алгоритмы работы с деревьями
Дерево – это иерархическая структура данных, состоящая из узлов (nodes), соединенных ребрами (edges). Один узел является корнем (root) дерева, а остальные узлы являются его потомками (children). Узел, не имеющий потомков, называется листом (leaf).
Алгоритмы работы с деревьями:
• Обходы дерева:
• Прямой обход (Preorder). Посещение корня, затем обход левого поддерева, затем обход правого поддерева.
• Центрированный обход (Inorder). Обход левого поддерева, затем посещение корня, затем обход правого поддерева (используется для отсортированных деревьев).
• Обратный обход (Postorder). Обход левого поддерева, затем обход правого поддерева, затем посещение корня.
• Кроме того, бывает еще и обход дерева в ширину Breadth-First Search, BFS. Посещение узлов по уровням.
Алгоритм начинает с корневого узла (первый уровень) и двигается по всем рёбрам, выходящим из него, перебирая последовательно каждый дочерний элемент (второй уровень). Когда все рёбра проверены, алгоритм переходит на следующий уровень и начинает перебирать дочерние элементы дочерних элементов (элементы третьего уровня) и так далее.
Для реализации алгоритма обхода дерева в ширину используется структура данных очередь. На каждом шаге извлекается из неё элемент, который был добавлен первым, и перебираются все его потомки. Каждый потомок также добавляется в очередь:
• Поиск элемента в дереве:
• Обычно используется для двоичных деревьев поиска (Binary Search Tree, BST).
• Сравнение искомого элемента с текущим узлом.
• Переход в левое поддерево, если искомый элемент меньше, или в правое поддерево, если искомый элемент больше.
• Вставка элемента в дерево: аналогично поиску.
• Удаление элемента из дерева: более сложный алгоритм, требующий перестройки дерева.
Примеры деревьев:
• Двоичное дерево поиска (BST).
• Сбалансированное дерево (AVL-дерево, красно-черное дерево).
• Дерево решений.
Для языков C# и Python нативных средств работы с деревьями нет, поэтому их нужно реализовать самостоятельно.
Реализация деревьев на C# и Python обычно предполагает создание классов для узлов дерева и методов для выполнения операций над деревом. Примеры реализации выходят за рамки данной статьи, но в интернете можно найти множество примеров реализации различных типов деревьев.
Хэш-таблица (она же хэш-карта, ассоциативный массив) - это структура данных, реализующая интерфейс ассоциативного массива, то есть позволяющая хранить пары «ключ-значение» и быстро находить значение по ключу. Хэш-таблицы широко используются в различных областях программирования, благодаря своей высокой эффективности при операциях поиска, вставки и удаления.
Основные принципы работы:
1. Хэш-функция: ключевым элементом хэш-таблицы является хэш-функция. Хэш-функция принимает ключ в качестве входных данных и возвращает хэш-код – целое число, представляющее собой индекс ячейки в массиве (который и является основной структурой хранения в хэш-таблице). Идеальная хэш-функция должна:
• быть детерминированной: для одного и того же ключа всегда возвращать один и тот же хэш-код;
• быстро вычисляться;
• равномерно распределять ключи по всему диапазону хэш-кодов, минимизируя коллизии (см. ниже).
2. Массив (бакеты): данные хранятся в массиве, каждая ячейка которого называется бакетом (bucket). Размер массива часто обозначается как N. Хэш-код, полученный от хэш-функции, используется для определения индекса бакета, в котором будет храниться пара «ключ-значение». Обычно хэш-код берется по модулю N (количество бакетов), чтобы получить индекс в пределах массива.
Вот как такая структура выглядит в памяти компьютера (иллюстрация):
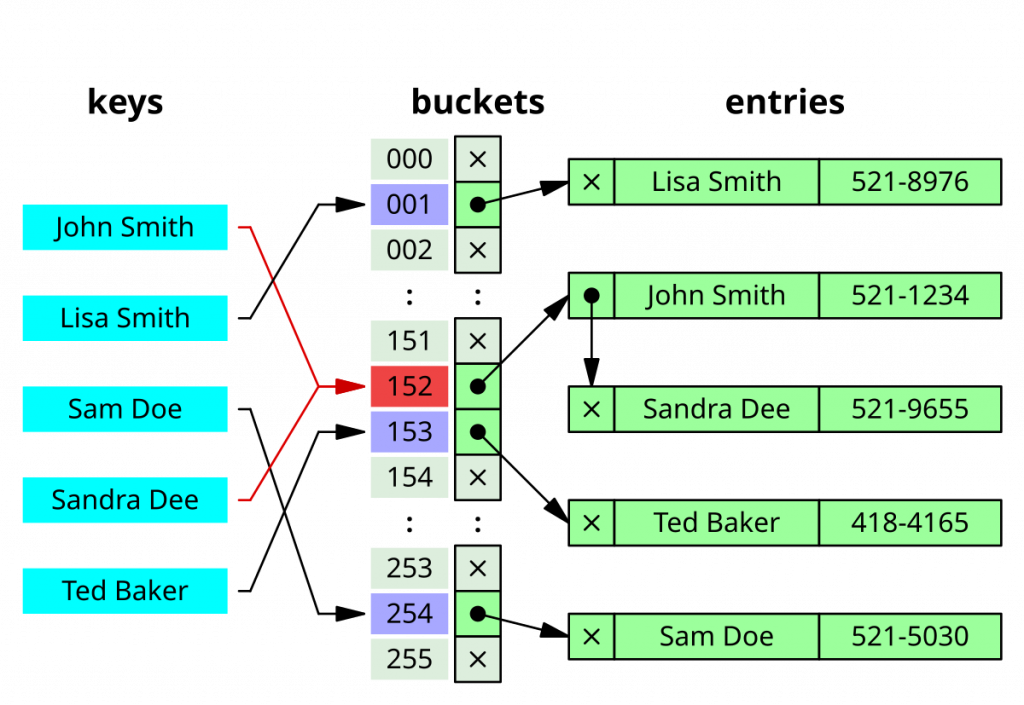
3. Коллизии: поскольку количество возможных ключей обычно намного больше, чем размер массива, коллизии неизбежны. Коллизия возникает, когда два разных ключа отображаются в один и тот же индекс массива (имеют одинаковый хэш-код по модулю N).
Существует несколько способов разрешения коллизий:
• раздельное связывание (Separate Chaining): каждый бакет хранит не одно значение, а список (связанный список или другую структуру данных) пар «ключ-значение», которые имеют одинаковый хэш-код. При поиске элемента в бакете происходит последовательный перебор списка.
• Открытая адресация (Open Addressing): если возникает коллизия, алгоритм ищет свободную ячейку в массиве. Наиболее распространенные методы открытой адресации:
Линейное пробирование (Linear Probing):* Поиск следующей свободной ячейки последовательно.
Квадратичное пробирование (Quadratic Probing):* Поиск свободной ячейки с использованием квадратичной функции.
Двойное хэширование (Double Hashing):* Использование второй хэш-функции для определения шага при поиске свободной ячейки.
Операции:
• Вставка (Insert): вычисление хэш-кода ключа, определение индекса бакета, добавление пары «ключ-значение» в этот бакет (с учетом разрешения коллизий).
• Поиск (Search): вычисление хэш-кода ключа, определение индекса бакета, поиск значения в этом бакете (с учетом разрешения коллизий).
• Удаление (Delete): вычисление хэш-кода ключа, определение индекса бакета, удаление пары «ключ-значение» из этого бакета (с учетом разрешения коллизий).
Характеристики:
• Средняя временная сложность:
• Вставка: O(1)
• Поиск: O(1)
• Удаление: O(1)
• Худшая временная сложность:
• Вставка: O(n) (в случае сильных коллизий, например, при использовании раздельного связывания с длинными списками).
• Поиск: O(n) (в случае сильных коллизий).
• Удаление: O(n) (в случае сильных коллизий).
• Пространственная сложность: O(n), где n – количество элементов, хранящихся в хэш-таблице.
Преимущества:
• высокая скорость доступа к данным: в среднем время доступа к элементам составляет O(1), что делает хэш-таблицы очень эффективными для поиска, вставки и удаления.
• простота реализации: основные принципы хэш-таблиц относительно просты для понимания и реализации.
• гибкость: хэш-таблицы могут хранить ключи и значения различных типов.
Недостатки:
• возможность коллизий: коллизии могут снизить производительность хэш-таблицы до O(n) в худшем случае.
• неупорядоченность: хэш-таблицы не сохраняют порядок элементов. Если вам важен порядок, используйте другие структуры данных, в частности, OrderedDict в Python или SortedDictionary в C#.
• зависимость от хэш-функции: эффективность хэш-таблицы сильно зависит от качества хэш-функции. Плохая хэш-функция может привести к большому количеству коллизий и снижению производительности.
• необходимость перехэширования (Resizing): при достижении определенного порога заполненности (load factor), необходимо увеличивать размер массива (перехэшировать), что может быть дорогостоящей операцией.
Реализация в различных языках:
• Python: встроенный тип данных dict (словарь) реализован как хэш-таблица.
• C#: класс Dictionary<TKey, TValue> реализован как хэш-таблица.
• Java: классы HashMap и Hashtable реализуют хэш-таблицы.
Когда использовать хэш-таблицы:
• когда требуется быстрый поиск, вставка и удаление элементов по ключу;
• когда порядок элементов не важен;
• когда количество элементов заранее неизвестно.
Примеры использования:
• кэширование: хэш-таблицы идеально подходят для кэширования данных, так как обеспечивают быстрый доступ к часто используемым значениям;
• индексирование: в базах данных хэш-таблицы могут использоваться для создания индексов, что позволяет быстро находить записи по определенным полям;
• реализация словарей и ассоциативных массивов: Python dict, C# Dictionary, Java HashMap и т.д.;
• счетчики частот: подсчет количества вхождений различных элементов в наборе данных;
• проверка уникальности: быстрая проверка, существует ли уже элемент в наборе.
Типизированные файлы (бинарные файлы)
Типизированные файлы — это файлы произвольного доступа, структура которых представляет собой последовательность компонентов одного типа. Одна из главных особенностей типизированного файла — возможность прямого обращения к его отдельным компонентам. Это достигается за счёт того, что заранее известен тип компонент файла.
Элементами типизированных файлов могут быть числовые, символьные, булевы, строковые значения, массивы, записи.
В отличие от текстовых файлов в типизированных (бинарных) файлах данные хранятся в двоичном формате, соответствующем их типу данных. Это позволяет более эффективно хранить данные и быстрее выполнять операции чтения/записи.
Алгоритмы для работы с типизированными файлами:
• чтение данных: чтение данных определенного типа (int, float, string, структура) из файла;
• запись данных: запись данных определенного типа в файл;
• позиционирование: перемещение указателя чтения/записи в определенную позицию в файле (для произвольного доступа к данным).
C#: BinaryReader, BinaryWriter, FileStream
Python: open('filename', 'rb'), open('filename', 'wb'), struct module (для упаковки и распаковки данных)
Пример реализации (C#):
using (BinaryWriter writer = new BinaryWriter(File.Open("data.bin", FileMode.Create)))
{
writer.Write(123); // Запись целого числа
writer.Write("Hello"); // Запись строки
}
using (BinaryReader reader = new BinaryReader(File.Open("data.bin", FileMode.Open)))
{
int number = reader.ReadInt32();
string text = reader.ReadString();
Console.WriteLine($"Number: {number}, Text: {text}");
}
Можно записать в бинарный файл целый объект. Правда, при этом он должен быть помечен как сериализуемый, то есть иметь атрибут Serializable.
Сериализация есть и в Python:
import struct
with open("data.bin", "wb") as f:
f.write(struct.pack('i', 123)) # Запись целого числа
f.write("Hello".encode()) # Запись строки (в байтах)
with open("data.bin", "rb") as f:
number = struct.unpack('i', f.read(4))[0] # Чтение целого числа
text = f.read().decode() # Чтение строки (в байтах)
print(f"Number: {number}, Text: {text}")
Сегодня мы рассмотрели важные аспекты анализа алгоритмов и их сложности. Мы узнали, зачем это нужно, как измерять эффективность алгоритмов и как динамические структуры данных могут помочь нам в решении различных задач.
Помните: правильный выбор алгоритма и структуры данных – это залог эффективной и быстрой работы вашей программы.
Вступайте в нашу телеграмм-группу Инфостарт