Анализ безубыточности с помощью Графа затрат

Вводная часть

Что такое безубыточная деятельность экономического субъекта? Понятие безубыточности, в сущности, сводится к простому тезису – доходы экономического субъекта должны превышать его расходы или как минимум равняться этим расходам, когда экономический субъект не получает ни прибыли, ни убытка.

Анализ безубыточности позволяет оценивать альтернативные варианты сценариев хозяйственной деятельности с точки зрения финансового результата и выбирать из них наиболее оптимальные. Остается только понять какими инструментами можно воспользоваться для проведения такого анализа. Далее в статье пойдет речь об использовании Графов затрат для решения данной задачи.

Несколько слов о теоретических основах анализа безубыточности (с замечаниями)

Перед тем, как перейти к примерам анализа безубыточности с помощью Графов затрат, кратко напомним некоторые теоретические положения по данной теме. Практически в любом учебнике по управленческому учету в той или иной степени рассматриваются методы оценки финансово-хозяйственной деятельности с точки зрения ее безубыточности – CVP-анализ (Costs, Volume, Profit), анализ взаимосвязи «затраты–объем–прибыль», операционный анализ, маржинальный анализ и т.п.

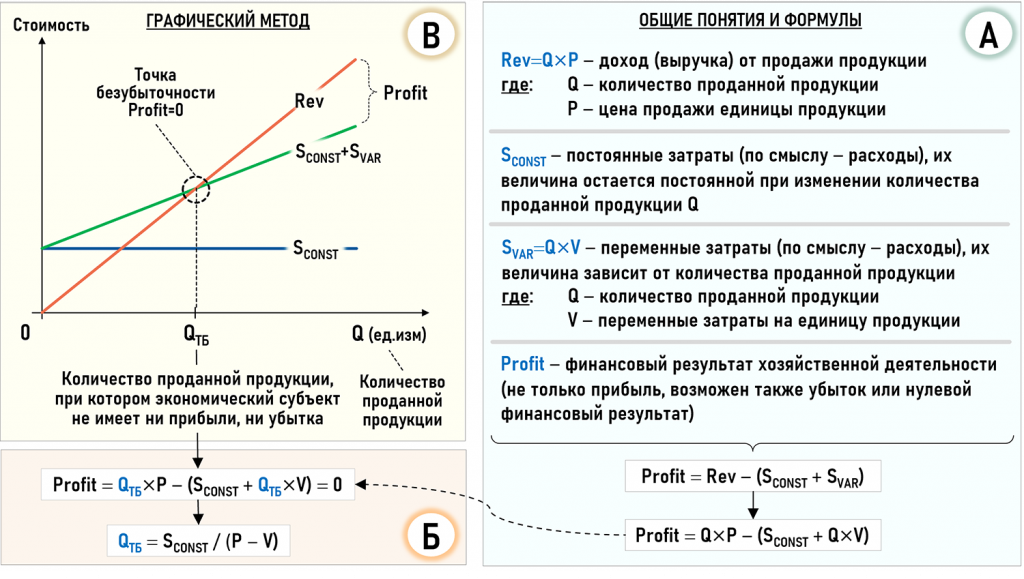
Названия разные, но смысловые различия между ними подчас настолько тонкие (вплоть до тождественности), а инструменты настолько похожи, что для целей данной статьи далее будем говорить просто об анализе безубыточности. Во всех перечисленных выше «анализах» используется ряд общих для них ключевых понятий (и уравнений), покажем их ниже на рисунке, сгруппировав в три блока – А, Б и В.

В блок А сгруппированы такие общие понятия, как доход, постоянные затраты, переменные затраты и финансовый результат, а также связывающие их уравнения, которые настолько очевидны, что не требуют дополнительных комментариев.

В блоке Б показано, как общие уравнения из блока А трансформируются для расчета точки безубыточности (break-even point – BEP), которую еще называют нулевой точкой, порогом рентабельности или порогом равновесия. Точка безубыточности определяет минимально допустимое количество проданной продукции, при котором доходом от ее продажи покрываются все расходы экономического субъекта на его хозяйственную деятельность.

В блоке В показаны графики, иллюстрирующие предполагаемое поведение рассмотренных выше величин при изменении количества проданной продукции. Эти графики также используются для нахождения точки безубыточности так называемым графическим методом. Определение точки безубыточности с помощью уравнений и графиков, представленных в блоках Б и В условно можно отнести к «классическим» вариантам анализа безубыточности, по крайней мере так мы их будем называть далее.

Казалось бы, все логично и понятно, и для проведения анализа безубыточности остается просто воспользоваться данной математической моделью (уравнениями и/или графиками). Но, как всегда, имеются «некоторые нюансы». Говорят, что уравнения любят, чтобы их разглядывали, и по результатам «разглядывания» представленных на рисунке уравнений сразу напрашивается вывод о том, что возможность их практического применения базируется на ряде весьма важных допущений. Рассмотрим некоторые из них.

1. Предполагается, что экономический субъект продает только один (базовый) вид продукции, так как рассмотренные выше уравнения (а также ось абсцисс системы координат для графиков) «работают» только с одной единицей измерения только одного вида продукции. Если же экономический субъект продает несколько видов продукции (многопродуктовое производство), то для использования данных уравнений придется разные виды продукции привести «к общему знаменателю», например, преобразовав количества и единицы измерения всех видов продукции в количество и единицы измерения базового вида продукции или некоей обобщенной единицы измерения опять же «обобщенного» вида продукции.

Проще говоря, если экономический субъект продает разные виды продукции (и услуг), измеряемые, например, в штуках, килограммах, литрах, метрах, комплектах, часах, машино-часах, тонно-километрах и т.п., то все эти единицы измерения необходимо привести к одной обобщенной, пусть даже и условной единице измерения, которую далее можно будет использовать как в уравнениях, так и для оси абсцисс системы координат для графиков. Причем формально одинаковые единицы измерения (например, штуки) разных видов продукции в данном случае также рассматриваются как разные единицы измерения, поскольку у этих видов продукции могут различаться как цены продажи единицы продукции, так и величины переменных затрат на единицу продукции.

2. Предполагается, что запасы готовой продукции и затраты в незавершенном производстве на конец исследуемого периода отсутствуют или считаются настолько несущественными, что ими можно пренебречь. Другими словами предполагается, что все затраты экономического субъекта в исследуемом периоде полностью попадают в готовую продукцию, в незавершенном производстве ничего не остается, а вся произведенная продукция продается. Это следует из того, что представленные выше уравнения и графики «работают» только с доходами и расходами, а затраты и расходы – это разные понятия. Так что для остатков готовой продукции и затрат в незавершенном производстве в этой модели просто нет места. В данном случае термины произведенная продукция и проданная продукция фактически можно считать тождественными.

3. Предполагается, что цена продажи единицы продукции максимально «устойчива», а проще говоря, она остается неизменной при продаже любого количества продукции. Никакие изменения рыночной ситуации, скидки и/или наценки за объем партии проданной продукции, наличие особых условий оплаты (сроки, этапы и т.п.) на цену продажи единицы продукции не влияют. Считается, что выполнение этого условия упрощает модель, позволяя легко прогнозировать поведение величины дохода при изменении количества проданной продукции, поскольку в данном случае эти величины связаны между собой линейной зависимостью.

4. Предполагается, что при производстве продукции не могут изменяться никакие характеристики производства (эффективность, производительность и т.п.), кроме количества выпускаемой продукции. Также остается неизменной и стоимость ресурсов для производства единицы продукции. Это позволяет считать, что величины постоянных затрат и переменных затрат на единицу продукции остаются неизменными для любого количества выпускаемой продукции. Это также упрощает модель, поскольку в этом случае обеспечивается линейный характер зависимости величины переменных затрат от количества проданной продукции.

Данный перечень основных допущений, собственно, и позволяет использовать такой простой «классический» вариант модели (уравнения и графики) для проведения анализа безубыточности. Однако допущения – это все-таки только предположения, истинность которых не обязательно должна быть доказана фактами. И в данном случае даже с первого взгляда понятно, что каждое из этих допущений хотя и упрощает модель для анализа безубыточности, но одновременно достаточно сильно искажает фактическое положение дел, и как следствие значительно ограничивает возможности широкого практического применения анализа безубыточности, по крайней мере в его «классическом» варианте.

Понятно, что в хозяйственной реальности экономические субъекты, производящие исключительно один вид продукции, встречаются не так уж и часто, как и варианты хозяйственной деятельности с полным отсутствием запасов готовой продукции и/или затрат в незавершенном производстве на конец периода. Цена за единицу продукции тоже редко остается неизменной для любого количества проданной продукции и условий ее продажи. Характеристики производства тоже обычно не остаются неизменными при увеличении количества производимой продукции, как и стоимость потребленных при этом ресурсов.

Что можно предпринять для того, чтобы сделать математическую модель для анализа безубыточности более актуальной условиям хозяйственной реальности? Для начала выясним – перечисленные выше допущения относятся к изначальным дефектам самой идеи анализа безубыточности или эти ограничения вызваны другими причинами? Очевидно, что к самой по себе идеи анализа безубыточности трудно предъявить какие-либо претензии, поскольку в ее основе лежит понятное желание экономического субъекта о превышении его доходов над расходами или как минимум об их равенстве. Претензии здесь можно предъявить только к «классическому» варианту практической реализации этой идеи, основанному на перечисленных выше допущениях.

Первое, что бросается в глаза при изучении данной темы в учебниках по управленческому учету, это слишком упрощенное отношение к такому ключевому понятию экономики, как экономический субъект. Создается впечатление, что все «богатого внутреннего мира» экономического субъекта особо никого не интересует, априори предлагается рассматривать экономический субъект как некий черный ящик. Например, в «классических» вариантах уравнений используется величина переменных затрат на единицу продукции. Откуда она берется? Обычно просто задается, иногда с дополнительной расшифровкой в виде списка входящих в нее затрат. При этом затраты не разделяются на первичные и вторичные, не поясняется как эти затраты попадают в себестоимость продукции, какие внутренние потоки затрат в этом участвуют, как они связаны с потоками затрат других видов продукции и как эти потоки затрат влияют друг на друга, об этом речь вообще не идет.

Понятно, что значения постоянных затрат и переменных затрат на единицу продукции обычно берутся не с потолка … наверное, но «внутренняя жизнь» экономического субъекта довольно сложна и для ее описания требуется адекватная математическая модель, которой в свою очередь для работы желательно иметь достоверные данные, полученные контролируемым способом. А иначе получается, что в «классическом» варианте уравнений (на выходе черного ящика) каким-то образом просто сразу задаются желаемые стоимости постоянных и переменных затрат (фактически расходов), при этом исключая из рассмотрения источники их появления – первичные затраты, внутренние маршруты движения потоков затрат (не только переменных, но и постоянных), их взаимосвязи с потоками затрат других видов продукции и/или услуг.

По мнению автора, от этих допущений (ограничений) можно если и не избавиться совсем, то существенно ослабить их влияние на построение математической модели для проведения анализа безубыточности. Для этого просто нужно ввести в математическую модель возможность расчета величин постоянных и переменных затрат с помощью Графа затрат, что в значительной степени может расширить область применения такой модели на практике. Далее будут рассмотрены примеры использования Графов затрат для проведения анализа безубыточности хозяйственной деятельности экономического субъекта.

Математическая модель для поиска сценария безубыточности

Сразу уточним, что поскольку далее в примере речь пойдет о многопродуктовом производстве (два вида проданной продукции), то искать мы будем не точку безубыточности, а сценарий безубыточности, поскольку при изменении количеств обоих видов проданной продукции могут меняться и другие параметры производственной программы.

Рассмотрим пример расчета сценария безубыточности для экономического субъекта, в организационной структуре которого выделены:

Цех1 – производит Продукцию1 (измеряемую в кг), весь объем которой в исследуемом периоде продается покупателям

Цех2 – производит Продукцию2 (измеряемую в кг), весь объем которой в исследуемом периоде продается покупателям

Цех3 – производит Продукцию3 (измеряемую в кг), которая используется в производстве Цехом1 и Цехом2, также на конец периода предусмотрен нормативный остаток Продукции3 на складе, равный количеству производимой за период Продукции1

Офис – административный персонал, стоимость управленческих услуг полностью включается в расходы исследуемого периода (direct-costing), количество (измеряемое в часах) управленческих услуг остается неизменным для любого количества проданной продукции (постоянные затраты)

Транспорт – транспортный цех, оказывает транспортные услуги (измеряемые в часах) остальным подразделениям. Для упрощения примера предполагается, что количества транспортных услуг для подразделений остаются постоянными при изменении количества проданной продукции (постоянные затраты)

Ремонт – ремонтный цех, производит ремонтные работы (измеряемые в часах) для производственных цехов и транспортного цеха. Для упрощения примера предполагается, что количества ремонтных работ для подразделений остаются постоянными при изменении количества проданной продукции (постоянные затраты)

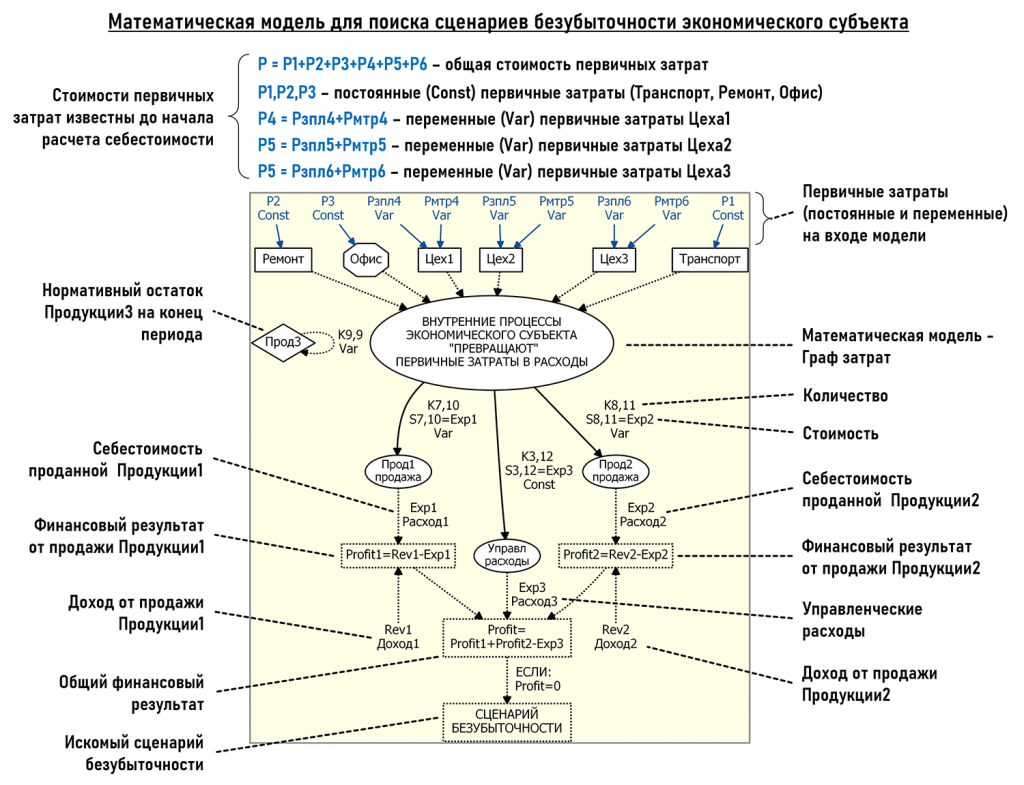
Рассмотрим обобщенную модель для проведения анализа безубыточности хозяйственной деятельности данного экономического субъекта.

На рисунке видно, что на «вход» экономического субъекта, то есть на «входы» его подразделений поступают первичные постоянные (Const) затраты и первичные переменные (Var) затраты. В данном примере их сразу удалось разделить, так как мы предположили, что количества управленческих услуг (Офис), транспортных услуг (Транспорт) и ремонтных работ (Ремонт) остаются постоянными при изменении количества проданной продукции.

Это сделано исключительно для упрощения примера, поскольку основной целью статьи является знакомство с математической моделью для анализа безубыточности на основе Графа затрат, так что лишние сложности здесь не нужны, главное понять принцип работы модели. Первичные переменные затраты для цехов дополнительно разделены на материальные затраты (мтр) и затраты на оплату труда (зпл), это поможет далее в процессе проведения анализа безубыточности.

Общий алгоритм работы данной модели можно описать следующим образом:

• на «входы» подразделений поступают первичные постоянные и переменные затраты
• далее они попадают в Граф затрат и по своим маршрутам доходят до расходов, то есть до себестоимости проданной Продукции1 и Продукции2, а также до управленских расходов Exp3 (direct-costing)
• где и «встречаются» с доходами от продажи продукции Rev1 и Rev2
• формируя финансовые результаты продажи каждого вида продукции Profit1 и Profit2
• а также общий финансовый результат Profit=Profit1+Profit2–Exp3
• если Profit=0, то это и будет искомый сценарий безубыточности

Это общее описание работы модели, но из него сразу понятно, что основная трудоемкость при проведении численного эксперимента по поиску сценария безубыточности будет связана с необходимостью многократного расчета себестоимости проданной продукции для различных параметров производственной программы. Другими словами, придется много раз решать СЛАУ. Выбор же алгоритма изменения цены продажи единицы продукции (а значит и дохода) и расчет финансовых результатов каких-либо особых сложностей в этой модели представлять не должны.

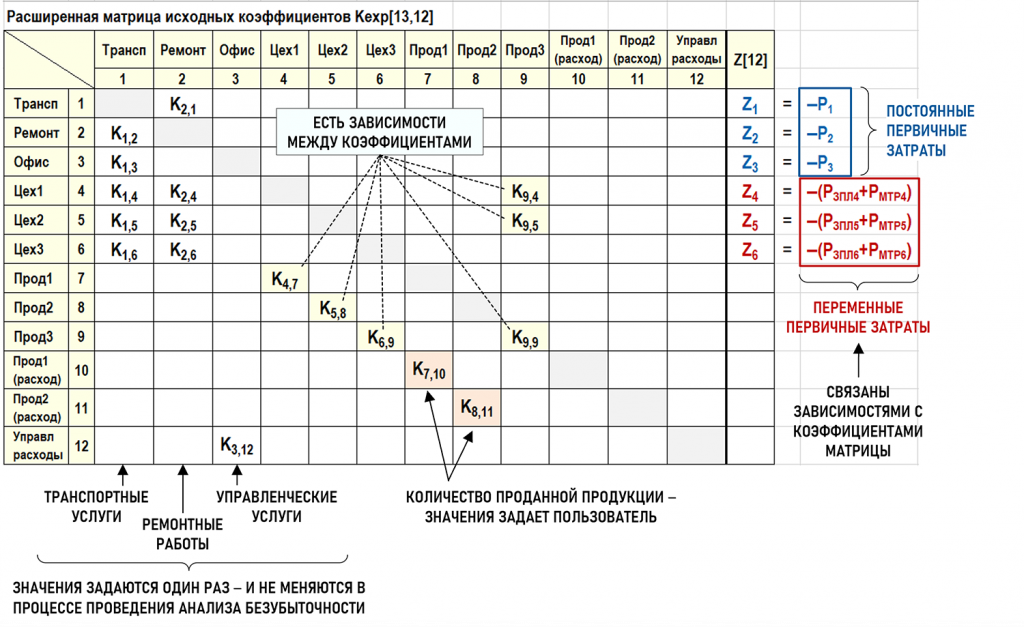
Поэтому в первую очередь далее уделим внимание фрагменту модели, в котором производится расчет себестоимости проданной продукции. Конкретизируем этот фрагмент, представив его в виде расширенной матрицы исходных коэффициентов (предполагается, что читатель знаком с данным видом матриц).

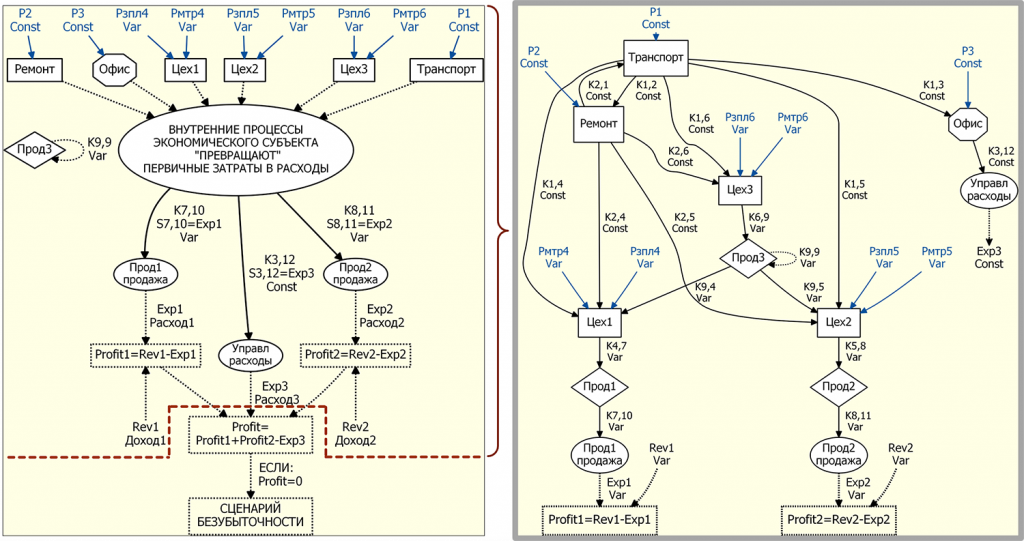
Также «расшифруем» этот фрагмент модели в графическом виде.

В процессе численного эксперимента можно задавать значения (в простейшем случае – вручную) исходных коэффициентов и первичных затрат, определяя в результате себестоимость любого количества проданной Продукции1 и Продукции2, а задав цену ее продажи, можно определить соответствующие финансовые результаты. Но гораздо проще проводить численный эксперимент в случае, если хотя бы часть исходных коэффициентов будет связана между собой какими-либо зависимостями. Это позволит уменьшить число задаваемых вручную значений исходных коэффициентов, поскольку значения остальных исходных коэффициентов будут определяться автоматически.

Для установления зависимостей между исходными коэффициентами необходим дополнительный анализ модели, посмотрим, как это может выглядеть на примере нашей расширенной матрицы исходных коэффициентов.

Поскольку вся произведенная Продукция1 и Продукция2 должна быть продана в исследуемом периоде, то сразу можно установить равенство значений для пар коэффициентов К4,7=К7,10 и К5,8=К8,11.

Поскольку условиями задачи было определено, что количество транспортных услуг остается постоянным при любом количестве проданной продукции, то значения коэффициентов в столбце Транспорт можно задать один раз и далее в численных экспериментах считать их неизменными. Аналогичная ситуация и со значениями коэффициентов в столбце Ремонт и в столбце Офис.

Все количество произведенной Продукции3 распределяется между Цехом1, Цехом2 и остатком Продукции3 на конец периода. Это значит, что количество произведенной Продукции3 (К7,10) равно сумме значений коэффициентов в столбце Прод3. Кроме того известно, что нормативный остаток Продукции3 на конец периода (К9,9) должен быть равен количеству производимой за период Продукции1 (К4,7).

Допустим также, что из системы нормативно-справочной информации (НСИ) экономического субъекта известно, что для производства одной единицы Продукции1 необходима одна единица Продукции3, это говорит о равенстве значений коэффициентов К9,4=К4,7. А для производства единицы Продукции2 необходимы две единицы Продукции3, то есть можно определить значение коэффициента К9,5= К5,8×2.

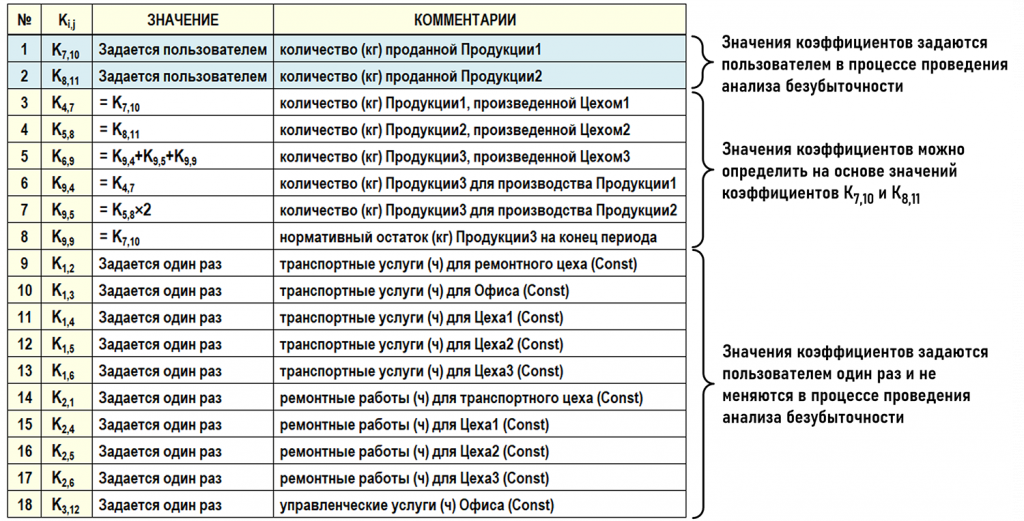
Подведем итоги первого этапа нашей аналитической работы. В первоначальном варианте в рассмотренной модели на каждом этапе численного эксперимента было бы необходимо задавать вручную значения 18-ти исходных коэффициентов. После анализа ситуации выяснилось, что значения 10-ти из них задаются только один раз и не меняются в процессе проведения численного эксперимента, а задав значения коэффициентов К7,10 и К8,11, значения оставшихся 6-ти коэффициентов получаются автоматически. Очевидно, что с таким вариантом модели работать гораздо удобнее. Сведем в таблицу полученные результаты.

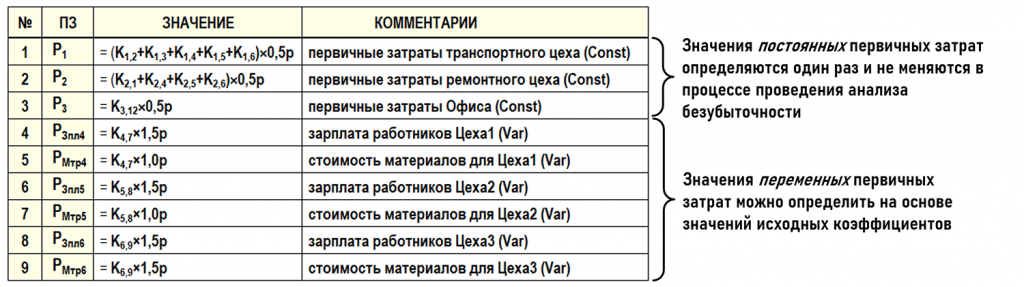
Теперь осталось разобраться со стоимостями первичных затрат, которые формируют правый столбец расширенной матрицы исходных коэффициентов. Для этого опять можно обратиться к системе НСИ экономического субъекта. Предположим, что каждый час работы транспортного цеха требует 0,5р первичных затрат (например, заработной платы и материальных затрат).

Этот показатель касается только первичных затрат и его несложно определить опытным путем и внести в систему НСИ. Умножив общее количество транспортных услуг на 0,5р получим общую стоимость первичных затрат транспортного цеха в исследуемом периоде. Аналогичную работу можно проделать и с остальными значениями первичных затрат, смысл действий здесь понятен, поэтому не будем их описывать подробно. Сведем в таблицу формулы для определения величин постоянных и переменных первичных затрат на основе значений исходных коэффициентов.

Итак, расширенная матрица исходных коэффициентов подготовлена для проведения численного эксперимента по поиску сценария безубыточности. Теперь можно только один раз задать значения 10-ти исходных коэффициентов в столбцах Транспорт, Ремонт и Офис, а далее на всех этапах численного эксперимента они останутся неизменными. Для определения значений остальных 8-ми исходных коэффициентов достаточно будет задавать значения К7,10 и К8,11, поскольку значения оставшихся 6-ти исходных коэффициентов будут определяться автоматически, как и стоимости первичных затрат.

Пример поиска сценария безубыточности

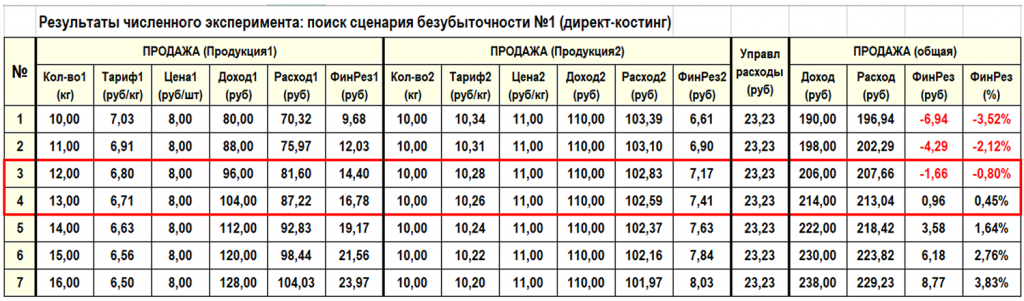
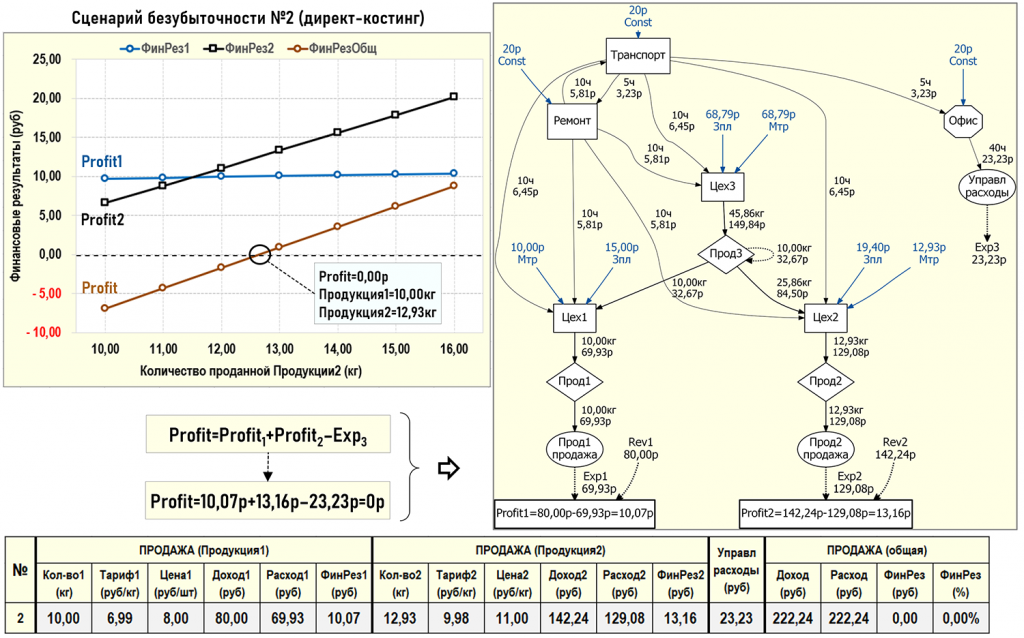
Для начала рассмотрим простой пример поиска сценария безубыточности. В данном численном эксперименте будем изменять только количество проданной Продукции1 в диапазоне [10кг...16кг] с шагом 1кг, оставив неизменным количество (10кг) проданной Продукции2. Цена продажи Продукции1 равна 8р/кг, цена продажи Продукции2 равна 11р/кг. Результаты численного эксперимента сведем в следующую таблицу.

На 4-ом этапе численного эксперимента общий финансовый результат поменял знак с «–» на «+», то есть сценарий безубыточности нужно искать в диапазоне значений проданной Продукции1 [12кг...13кг]. Далее можно вручную уменьшить шаг поиска решения и продолжить численный эксперимент в найденном диапазоне, а можно (и лучше) воспользоваться одним из методов оптимизации.

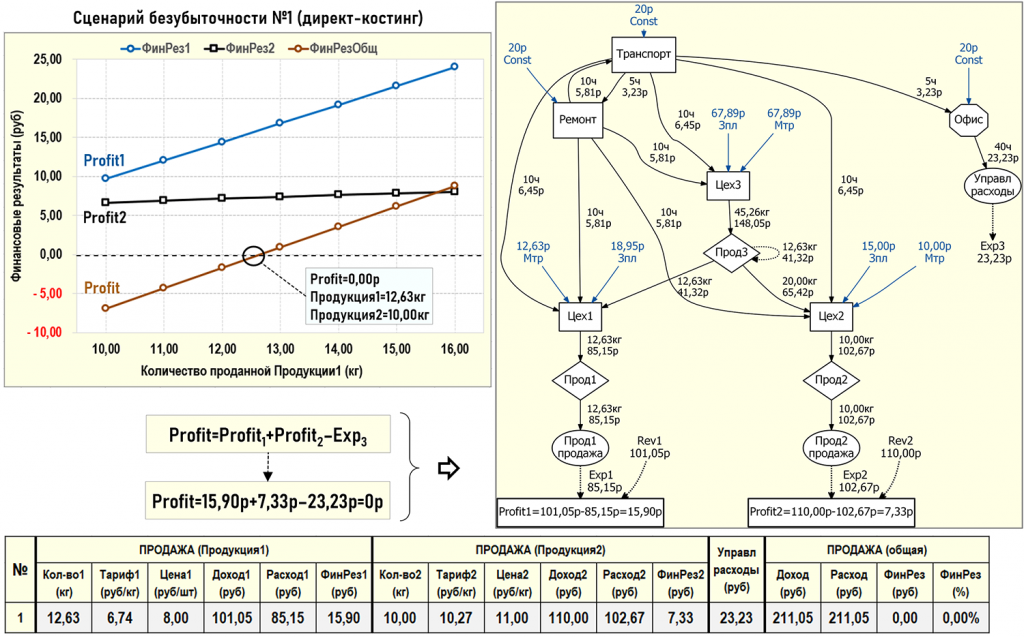
Например, данная задача решалась в Excel и для поиска сценария безубыточности была использована надстройка Поиск решения, в которой был выбран метод обобщенного понижающего градиента (ОПГ). В процессе поиска решения изменялось количество проданной Продукции1 (К7,10) пока не было с приемлемой точностью достигнуто 0-вое значение общего финансового результата Profit. Результат поиска сценария безубыточности представлен ниже на рисунке (время поиска решения менее 1с).

Также на рисунке представлены графики, иллюстрирующие изменение значений финансовых результатов Profit1, Profit2 и Profit в зависимости от количества проданной Продукции1. Пересечение графика Profit с 0-лем по оси ординат определяет искомый сценарий безубыточности.

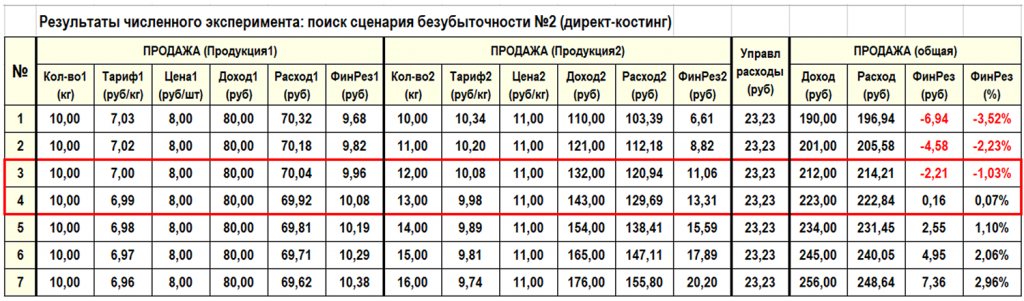
Проведем еще один численный эксперимент, в котором будем изменять только количество проданной Продукции2 в диапазоне [10кг...16кг] с шагом 1кг, оставив неизменным количество (10кг) проданной Продукции1. Цены продажи Продукции1 и Продукции2 также остались равны 8р/кг и 11р/кг соответственно. Результаты численного эксперимента сведем в следующую таблицу.

Опять на 4-ом этапе численного эксперимента общий финансовый результат поменял знак с «–» на «+», то есть сценарий безубыточности нужно искать в диапазоне значений проданной Продукции2 [12кг...13кг].

Опять воспользуемся методом ОПГ, для поиска решения изменялось количество проданной Продукции2 (К8,11) пока не было с приемлемой точностью достигнуто 0-вое значение общего финансового результата Profit. Результат поиска сценария безубыточности представлен ниже на рисунке (время поиска решения также оказалось менее 1с).

Как видим, решение простых задач, когда при поиске сценария безубыточности для многопродуктового производства изменяется количество только одного вида продукции, не должно вызывать особых проблем. Теперь усложним условия задачи.

Поиск множества сценариев безубыточности

Поскольку экономический субъект продает два вида продукции (многопродуктовое производство), то можно предположить, что для разных комбинаций количеств этих видов проданной продукции можно получить разные варианты сценариев безубыточности. Проверим это предположение с помощью численного эксперимента.

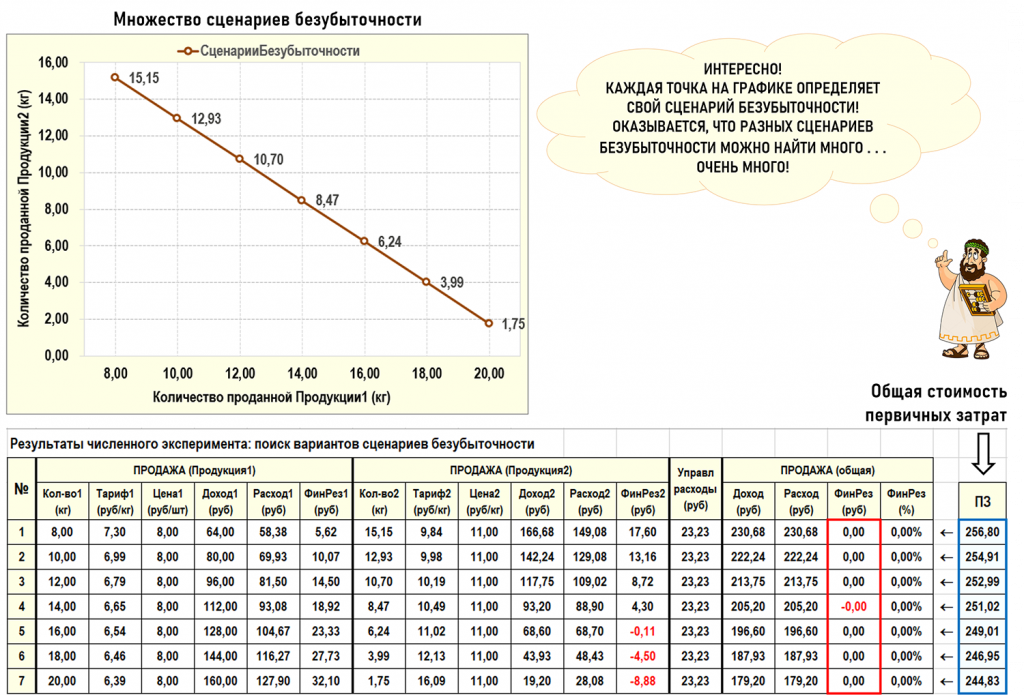
Будем изменять количество проданной Продукции1 в диапазоне [8кг...20кг] с шагом 2кг, и на каждом шаге будем искать (методом ОПГ) количество проданной Продукции2, при котором будет достигнут сценарий безубыточности. Результаты численного эксперимента представлены ниже на рисунке.

Как видим, результаты численного эксперимента подтвердили предположение о том, что даже всего для двух видов проданной продукции можно найти множество вариантов сценариев безубыточности. В частности, это означает, что поиск нулевого финансового результата является здесь только частью задачи, поскольку возможен учет и других факторов для выбора искомого сценария безубыточности.

Например, 7-ой сценарий безубыточности выполняется при минимальном значении первичных затрат, что может оказаться решающим для выбора именно этого сценария безубыточности. Но могут оказывать влияние и другие факторы – потребности рынка, договоренности с контрагентами и т.д. В любом случае понятно, что в случае многопродуктового производства сама по себе задача поиска сценария безубыточности является только частью более объемной задачи, связанной с выбором оптимального сценария безубыточности из множества альтернативных вариантов, поскольку необходимо учитывать влияние на этот выбор и других факторов, помимо достижения нулевого общего финансового результата.

Выводы

В рассмотренных в начале статьи «классических» вариантах анализа безубыточности используются достаточно простые математические модели – уравнения и/или графики. Эта «простота», безусловно, привлекательна и вполне понятно желание учетных специалистов использовать именно эти математические модели. Но будем откровенны, эта простота опирается на слишком уж жесткие допущения, слишком серьезно приходится подстраивать хозяйственную реальность под эти «классические» уравнения и/или графики, чтобы ими можно было реально широко пользоваться на практике.

Модель для анализа безубыточности на основе Графа затрат снимает значительную часть «жесткости» этих допущений, позволяя включить в процесс анализа безубыточности внутренние процессы экономического субъекта, выраженные с помощью потоков затрат, что позволяет, например, без особых сложностей искать сценарии безубыточности для многопродуктовых производств. Также данная модель не требует наличия строго линейных зависимостей величин доходов и расходов от количества проданной продукции. В примерах для простоты мы использовали именно такой вид зависимости, но на практике эти зависимости могут принимать в модели любой вид – нелинейный, кусочно-непрерывный и т.п.

IT-технологии очень быстро меняют (должны менять) учетную деятельность, перспективы профессии учетного специалиста существенно зависят от его способности адаптироваться к этим изменениям. Развитие IT-технологий позволяют «привлекать» в учетную деятельность все больше математических моделей разной степени сложности, использовать различные численные методы, в нашем случае это численные методы решения СЛАУ и оптимизации. Эти численные методы с успехом применяются на практике в разных областях деятельности как минимум с середины прошлого века, поэтому достаточно сложно найти разумные аргументы против их использования в рассматриваемой предметной области (микроэкономике) и, в частности, в математической модели для анализа безубыточности.