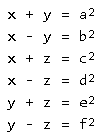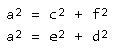Function zNumber(Re,Im) Export
arr=new array();
arr.Add(Re);
arr.Add(Im);
return arr;
EndFunction
Function zMult(a,b) Export
arr=new array();
arr.Add(a[0]*b[0]-a[1]*b[1]);
arr.Add(a[0]*b[1]+a[1]*b[0]);
return arr;
EndFunction
Аргументы функции - два комплексных числа, возвращаемое значение двумерный массив. Следующая функция позволяет возвести комплексное число в целую степень.
Function zPower(z,p) Export
if p=0 then
arr=new array;
arr.Add(1);
arr.Add(0);
return arr;
endif;
if p=1 then
return z;
endif;
if (p%2)=0 then
t=zPower(z,p/2);
return zMult(t,t);
endif;
return zMult(zPower(z,p-1),z);
EndFunction
В приведенном коде мы пытаемся сократить требуемое количество операций умножения, заменяя четные степени возведением в квадрат. А вот еще одна элементарная функция, которая возвращает число сопряженное данному.
Function zConjugate(z) Export
arr=new array();
arr.Add(z[0]);
arr.Add(-z[1]);
return arr;
EndFunction
- 65=1*1+8*8
- 65=4*4+7*7
- 5 =1*1+2*2
- 13=2*2+3*3
Function zGenerateVar(z,p) Export
arr=new array;
zCon=zConjugate(z);
arr.Add(zPower(z,p));
for i=1 to (p-1) do
arr.Add(zMult(zPower(z,i),zPower(zCon,p-i)));
enddo;
arr.Add(zPower(zCon,p));
return arr;
EndFunction
Функция РазложитьНаПростыеМножители(вхЧисло,ПростыеЧисла)
тЧисло=новый ОписаниеТипов("Число",,,новый КвалификаторыЧисла(19,0));
разложение=новый ТаблицаЗначений;
разложение.Колонки.Добавить("Множитель",тЧисло);
разложение.Колонки.Добавить("Степень",тЧисло);
если ПростыеЧисла.Найти(вхЧисло)<>Неопределено тогда
нСтр=разложение.Добавить();
нСтр.Множитель=вхЧисло;
нСтр.Степень=1;
возврат разложение;
конецесли;
Граница=(вхЧисло-вхЧисло%2)/2;
для каждого число из ПростыеЧисла цикл
если число > Граница тогда
прервать;
конецесли;
если вхЧисло%число=0 тогда
нСтр=разложение.Добавить();
нСтр.Множитель=число;
нСтр.Степень=1;
н=число*число;
пока вхЧисло%н=0 цикл
нСтр=разложение.Добавить();
нСтр.Множитель=число;
нСтр.Степень=1;
н=н*число;
конеццикла;
конецесли;
конеццикла;
разложение.Свернуть("Множитель","Степень");
возврат разложение;
КонецФункции
Decompose=РазложитьНаПростыеМножители(i,PrimeNumber);
arr.Clear();
Q=1; test=0;
for each row in Decompose do
n=row.Множитель;
p=row.Степень;
if n=2 then
z=zNumber(1,1);
vc=new array;
vc.Add(zPower(z,p));
arr.Add(vc);
else
find=vt.Find(n,"N");
if find.a=0 then
if p%2=1 then
test=0;
break;
endif;
Q=Q*n;
for j=2 to p do
Q=Q*n;
enddo;
else
test=test+1;
z=zNumber(find.a,find.b);
arr.Add(zGenerateVar(z,p));
endif;
endif;
enddo;
Function zSquare(arr,level,mult,Q)
if level = arr.Count() then
z=mult[0];
imax=arr.Count()-1;
for i=1 to imax do
z=zMult(z,mult[i]);
enddo;
z0=z[0]*z[0];
z1=z[1]*z[1];
if z0*z1>0 then
row=GaussPairs.Add();
if z0>z1 then
row.a=Q*z0;
row.b=Q*z1;
else
row.a=Q*z1;
row.b=Q*z0;
endif;
endif;
return true;
endif;
for each z in arr[level] do
mult[level]=z;
zSquare(arr,level+1,mult,Q);
enddo;
EndFunction
Аргументы функции это:
- массив с вариантами arr;
- переменная level говорит о том с каким элементом данного массива мы работаем на текущем шаге;
- mult - массив в нем мы собираем все множители разложения;
- назначение переменной Q мы объяснили в предыдущем абзаце.
Найдите целые числа x > y > z > 0 такие, что x + y, x - y, x + z, x -z, y + z, y-z все являются квадратами целых чисел.
Введем обозначения: