Задача, рассматриваемая в статье, приводится здесь с разрешения ее автора Ish_2. Собственно задача была сформулирована в ходе обсуждения вопроса "Реально написать хитрый запрос" в посте (79) примерно так:
Дана таблица, содержащая три колонки: номенклатура-набор (X), номенклатура-элемент (Y), количество элементов в наборе (Z). В строчках этой таблицы записаны тройки (X, Y, Z):
Всего таблица содержит 61 элемент ("0", А0, ..., А9, Б0, ... , Б9, ... , Е0, ... , Е9) и 510 строк:
(0, А0, 2) (0, А1, 2) (0, А2, 2) (0, А3, 2) (0, А4, 2) (0, А5, 2) (0, А6, 2) (0, А7, 2) (0, А8, 2) (0, А9, 2)
(А0, Б0, 2) (А0, Б1, 2) (А0, Б2, 2) (А0, Б3, 2) (А0, Б4, 2) (А0, Б5, 2) (А0, Б6, 2) (А0, Б7, 2) (А0, Б8, 2) (А0, Б9, 2)
(А1, Б0, 2) (А1, Б1, 2) (А1, Б2, 2) (А1, Б3, 2) (А1, Б4, 2) (А1, Б5, 2) (А1, Б6, 2) (А1, Б7, 2) (А1, Б8, 2) (А1, Б9, 2)
...
(Д9, Е0, 2) (Д9, Е1, 2) (Д9, Е2, 2) (Д9, Е3, 2) (Д9, Е4, 2) (Д9, Е5, 2) (Д9, Е6, 2) (Д9, Е7, 2) (Д9, Е8, 2) (Д9, Е9, 2).
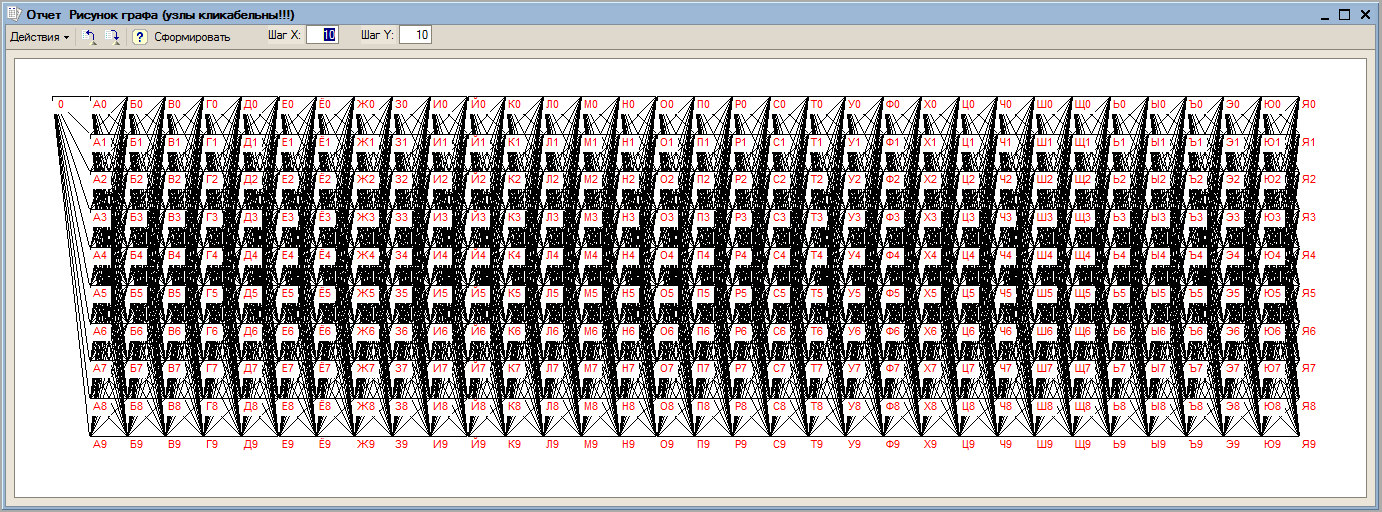
Каждая строка таблицы (X, Y, Z) интерпретируется следующим образом: объект X содержит элемент Y в количестве Z. Наглядно эта таблица представляется следующим графом (фиг1). Все дуги на фиг1 направлены слева направо и имеют вес, равный двум.

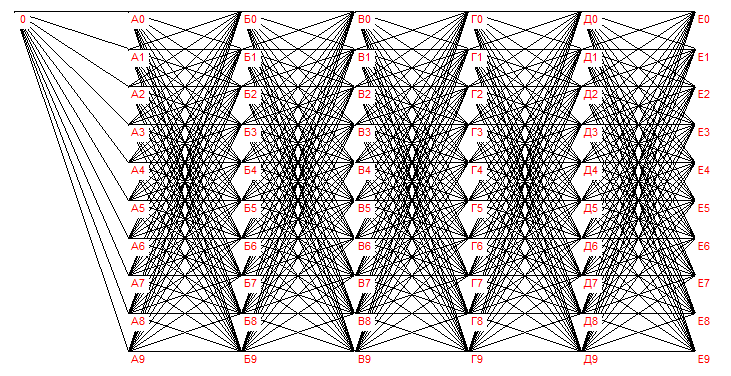
Требуется построить программу, способную посчитать: сколько элементов Е0, Е1, Е2, Е3, Е4, Е5, Е6, Е7, Е8, Е9 содержится в объекте «0». Конечно, программа должна решать подобные задачи в общем случае для всех подобных таблиц. Тогда данный пример будет тестом скорости работы программы, а также правильности алгоритма путем сравнения с очевидным ответом (6 400 000, 6 400 000, … , 6 400 000). В этом общем случае программа также должна исключать ошибочные связи типа Е9 – 0, Д0 – Б9 и другие «обратные» связи, приводящие к «зацикливанию».
Сравнение строк 11 (А0-Б0-2) и 21 (А1-Б0-2) позволяет сделать принципиально важный вывод: структура, описываемая таблицей, не является деревом! Элемент Б0 имеет более одного владельца! Необходимость такой структуры при составлении сборочных спецификаций легко объяснить: если четыре колеса входят в спецификацию автомобиля, а два таких же колеса в спецификацию прицепа, то заводится не две разных, а одна единая спецификация колеса. В результате шина как элемент колеса входит в состав автомобиля с прицепом двумя различными способами: в составе колеса в составе автомобиля и в составе колеса в составе прицепа.
В тестовом примере элемент Е9 входит в состав элемента «0» сто тысячью (100 000) различных способов! Вот тут-то некоторые программисты и делают принципиальную ошибку: они считают, что для подсчета числа вхождений Е9 нужно перечислить все 100 000 способов. (На самом деле это тоже самое, что вычислять 10 х 10 х 10 х 10 х 10 х 10 миллионом сложений единиц!) Источником этой ошибки, видимо, является известный отчет о разузловании, строчки которого соответствуют путям вхождения атомарных деталей в готовое изделие. Отчет для наглядности представляется в виде дерева. В данном случае это дерево отчета будет иметь миллион конечных вершин. Видимо, тут и возникает желание получить результат поставленной задачи группировкой этих путей по виду их конечных элементов. Как же по-другому? – А вот как:
1. Исходная задача разузлования заданного узла разбивается на более простые задачи разузлования отдельных узлов, причем в этих простых задачах считается, что результат разузлования подчиненных узлов уже известен. Тогда результат разузлования узла получается как сумма результатов разузлования подчиненных узлов, взятых с коэффициентом количества для каждого подчиненного узла. Если обозначить результат разузлования узла j как Q(j) = (q1j, q2j, … , qNj), где qij обозначает, что узел j транзитивно содержит узел i qij раз, и если как gkl обозначить количество узлов i в спецификации узла k, то получаем простую формулу подсчета результата разузлования узла k
Q(k) = ∑ i=1,N G’(i) * Q(i) = ∑ i=1,N gki * qij. (1)
2. Результат разузлования каждого узла запоминается, чтобы не вычисляться заново. Поэтому в решении тестовой задачи будет всего 51 операция вида (1).
3. Порядок обхода вершин графа, начиная с заданного, определяется рекурсией. Дважды в один и тот же узел для расчетов алгоритм не входит!
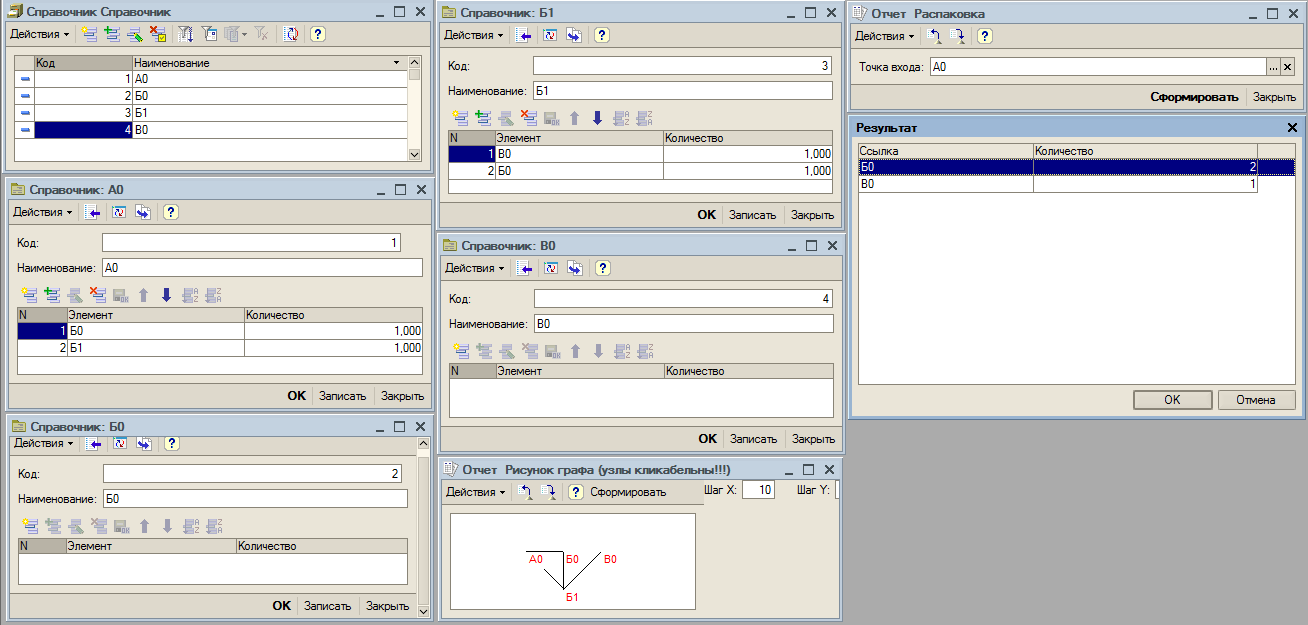
Вот конфигурация справочника, в котором хранится таблица (фиг2)
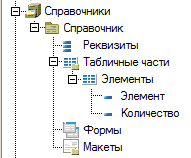
А вот код самой программы (фиг3)

Приведен весь исходный код. Никакого другого кода в решении нет и он не требуется.
Для работы с относительно небольшими структурами достаточно использовать массивы.
В данном случае используется массив массивов Матрица. Измерениями будет номер вершины графа. Для простоты считаем, что коды вершин начинаются с единицы и не содержат пропусков. Это позволяет рассчитать индекс при обращении к массиву как ё = Ссылка.Код – 1. В результате Матрица[ё] будет содержать разузлование узла Ссылка. Если Матрица[ё][0] = Неопределено, значит, этой вершиной еще не занимались. Сначала разузлование обнуляется //процедура Обнулить()//, затем к нему в цикле прибавляются разузлования подчиненных узлов //определяемые рекурсивно процедурой Распаковать()// с соответствующим весом //процедура Добавить()//. После разузлования подчиненных узлов отмечаем единицей текущий узел //Матрица[ё][ё] = 1//. Этой единицей данный узел будет с точки зрения вышележащих уровней.
Если разузлование находится в процессе расчета //Матрица[ё][0] <> Неопределено//, но не закончено, то Матрица[ё][ё] = 0. Это дает возможность проверить зацикливание. Правда диагностический вывод «слабоват» - мы отмечаем только вершину, в которую попали в результате «зацикливания».
Запрос в начале работы программы нужен только для построения таблицы, куда потом будут помещены результаты работы метода, для определения терминальных узлов, а также для определения количества узлов, которое также определяет размерность массива.
Для того, чтобы работать со структурами, не помещающимися в массив или сильно разреженными, нужно хранить промежуточные разузлования в массиве не как вложенные массивы, а как таблицы значений и переписать процедуры Обнулить() и Добавить(). Выполнение, возможно, даже не замедлится. Опытным путем можно попробовать установить, что и для каких размерностей лучше.
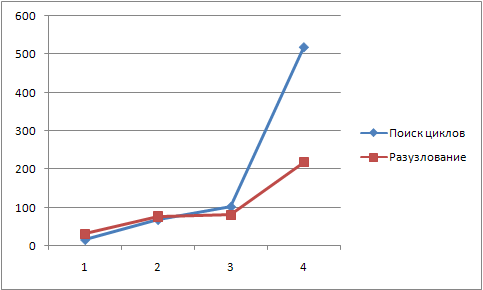
Сейчас тестовая задача выполняется примерно 0,122 секунды (использовалась платформа 8.1 и ноутбук). При этом «неправильные» методы дают на два-три порядка большие значения!
Сформировав структуру степени 10 из 33 уровней (331 вершина), получим время разузлования всего 3,666 секунды!
К статье прилагается конфигурация, содержащая справочник описанной структуры и отчет с исходным кодом решения (в варианте использования массива). Кроме того, конфигурация содержит обработку, позволяющую формировать тестовые структуры по заданному алфавиту и степени графа (числа ветвей в разветвлении). Там же имеется отчет, позволяющий нарисовать структуру графа, тип которого рассматривается в статье.
Если никто не вспомнит, где уже встречалось такое решение, мне будет нетрудно перевести его на 77. Там всего лишь несколько более длинный код. Также возможно будет интересным показать, как решается эта задача с использованием техники «одного запроса».
Вступайте в нашу телеграмм-группу Инфостарт