Разумеется, значительно легче отвечать на вопрос, если ты заранее знаешь ответ. В этом и кроется причина популярности сервисов, которые предлагают список возможных тестов и задач. Не знаю, встречалась ли такая задача на собеседовании, но расширить свой багаж не будет лишним. Необходимо найти выражение для суммы квадратов N первых положительных целых чисел, используя Excel. Формула эта давно известна, но вряд ли большинство людей держат ее в памяти. Выводится она с помощью следующего равенства:
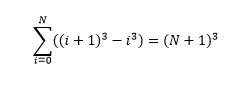
Что интересно, Ричард Фейнман будучи школьником решил задачу нахождения суммы степеней последовательных целых чисел и очень расстроился, когда узнал, что тоже самое сделал Бернулли за триста лет до него.
В задании надо эту формулу подобрать. Итак, открываем Excel, строим следующую таблицу.
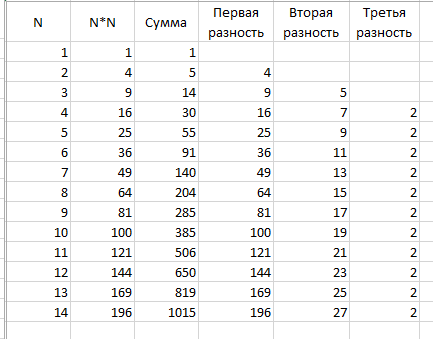
В первой колонке число, во второй его квадрат, в третьей идет сумма квадратов. В колонке Первая разность хранится разность соседних ячеек из колонки Сумма. Это квадраты числа из первой колонки, так оно и должно быть, это очевидно. В колонке Вторая разность отображается разность соседних ячеек из колонки Первая разность. Это нечетные числа, и это говорит о том, что квадрат любого числа, есть сумма последовательных нечетных чисел. Теперь несложно догадаться, что находится в колонке Третья разность. Тот факт, что все значения в этой колонке одинаковые, говорит нам о том, что зависимость выражения для суммы квадратов от верхнего предела N есть многочлен третьей степени. И это действительно так.

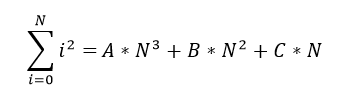
В общем случае в формуле должен присутствовать свободный член, но так как при N=0 сумма равна нулю, то он отсутствует. Первое следствие из данной формулы - сумма делится на число N. Проверяем по нашей таблице и убеждаемся, что это не так. Ошибка в формуле ? Нет, формула верна. Все дело в том, что наше первоначальное предположение справедливо, если только все числа A,B и C целые. А это, по-видимому, не так. Верным будет следующее утверждение - сумма умноженная на целое число делится на N. И это число находится простым перебором, оно равно 6.
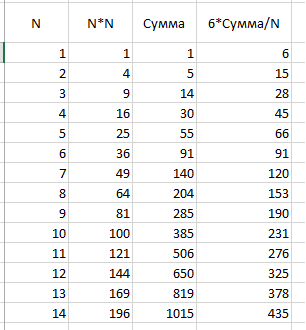
Ну и заключительный шаг. Разложим число из колонки 6*Сумма/N на два множителя. Первые числа небольшие и сделать это нетрудно.
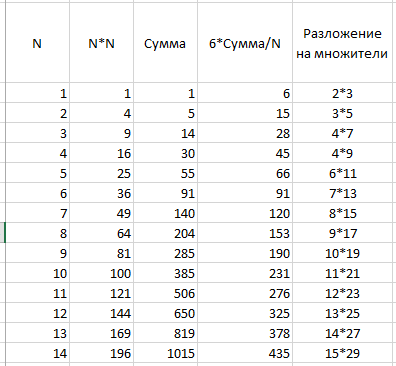
Уже после первых трех строк становится понятна итоговая зависимость.
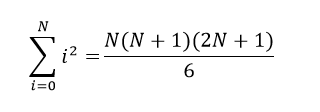
Ну и ответ на вопрос "Какое это имеет отношение к 1С ?". Дело в том, что периодически я сталкиваюсь с ситуацией, когда на собеседовании задают вопросы, которые предполагают не кодирование в "лоб", ибо это приведет к тому, что время выполнения задачи станет неразумно большим, а применение, зачастую, элементарного математического аппарата, что позволяет достигнуть значительного ускорения. Согласитесь, что цикл от единицы до миллиарда для нахождения суммы квадратов будет выполняться очень долго.
Вступайте в нашу телеграмм-группу Инфостарт