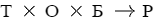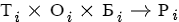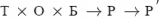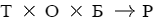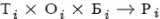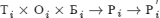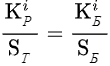Содержание
Введение
Проведем следующий эксперимент. Скопируйте код ниже в консоль выполнения. В этом коде использованы два алгоритма распределения: с отнесением погрешности на максимальный коэффициент и рекурсивный с уменьшением базы. Возмем сумму распределения меньше суммы базовых коэффициентов. В первом алгоритме в результате распределения на последнем коэффициенте получилось число больше исходного значения, что нарушает базовое ограничение модели распределения.
Физически это можно представить так: пусть есть некоторое количество вещества, разложенного по компонентам в долях. Необходимо получить разложения вещества для меньшего общего количества. Если в результате получится превышение в какой-то доле исходного вещества, то физически такое распределение сделать не удасться.
На этом примере иллюстрируется важность ограничения по базе. Если распределяемая сумма меньше или равна сумме коэффициентов, то в результате распределения для коэффициентов также должно соблюдаться условие: результат не должен превышать исходное значение. Для распределения суммы больше исходного значения такого ограничения нет, но ожидается, что распределение погрешности будет равномерным, но это уже предмет другого исследования.
Базовые ограничения модели реализуются через виды распределения.
Пример кода на сравнение алгоритмов распределения
// Инициализация
Коэффициенты = ОбщийКлиентСервер.JSONВОбъект("[1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 3]");
Сумма = РаботаСМассивом.Преобразовать(Коэффициенты, "Накопитель + Элемент", 0, 0);
РаспределяемаяСумма = Сумма - 0.08;// распределяемая сумма меньше суммы коэффициентов
// Получение результата распределения
РезультатСОтнесениемНаМакс = ОбщегоНазначения
.РаспределитьСуммуПропорциональноКоэффициентам(РаспределяемаяСумма, Коэффициенты, 2);
РезультатСУменьшениемБазы = РаботаСМассивом.РаспределитьСумму(РаспределяемаяСумма, Коэффициенты, 2);
// Вывод результата
Сообщить(СтрШаблон("Сумма: %1, РаспределяемаяСумма: %2", Сумма, РаспределяемаяСумма));
Сообщить(ОбщийКлиентСервер.ОбъектВJSON(Коэффициенты));
Сообщить(ОбщийКлиентСервер.ОбъектВJSON(РезультатСОтнесениемНаМакс));
Сообщить(ОбщийКлиентСервер.ОбъектВJSON(РезультатСУменьшениемБазы));
Сравнение результатов алгоритмов распределения
Распределение
Виды распределения
Модель распределения поддерживает виды распределения: по порядку, по базе и полное. Первые два ограничены коэффициентами базы. Это означает, что в результате распределения полученные коэффициенты будут меньше либо равны исходным. Полное распределение не имеет такого ограничения и позволяет получить результат в пропорции:
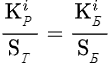
, где K - коэффициент, S - сумма, Т - таблица, Р - результат, Б - база, i - шаг
Попробовать различные варианты распределения можно в демо обработке "Демо диаграмма распределения":
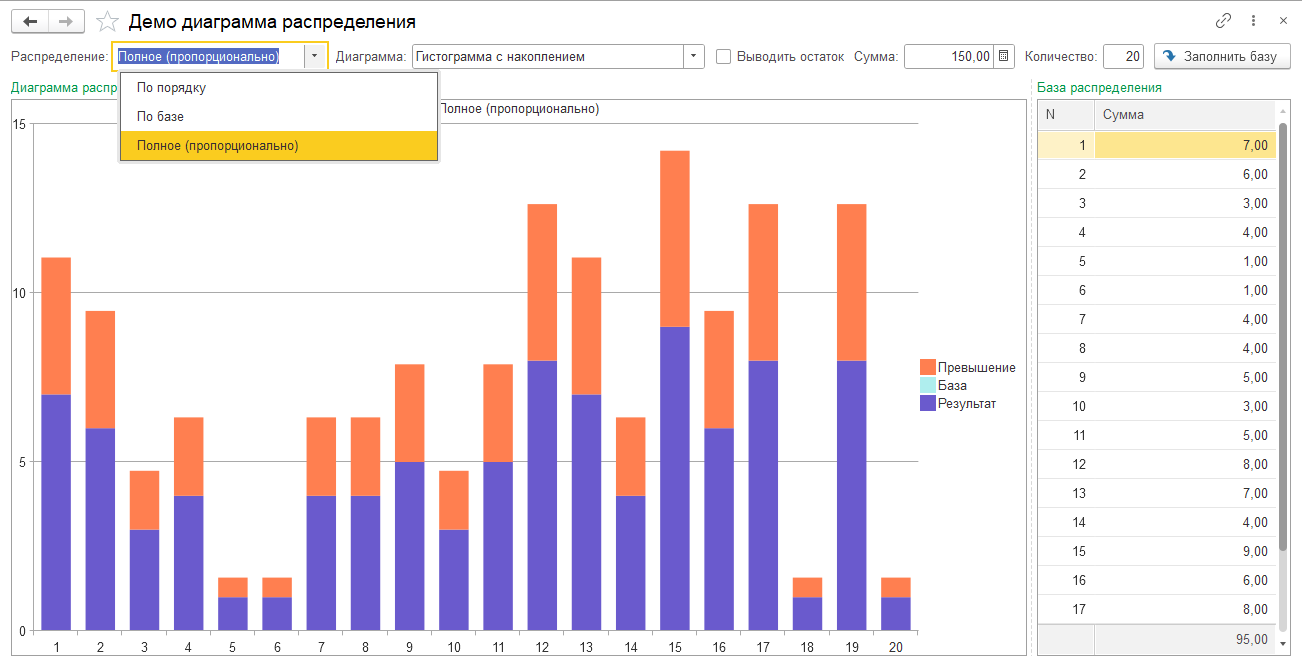
Демо диаграмма распределения
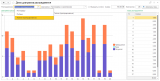
На следующих диаграммах показаны три варианта распределения для случаев: сумма распределения не превышает сумму базовых коэффициентов и когда превышает:
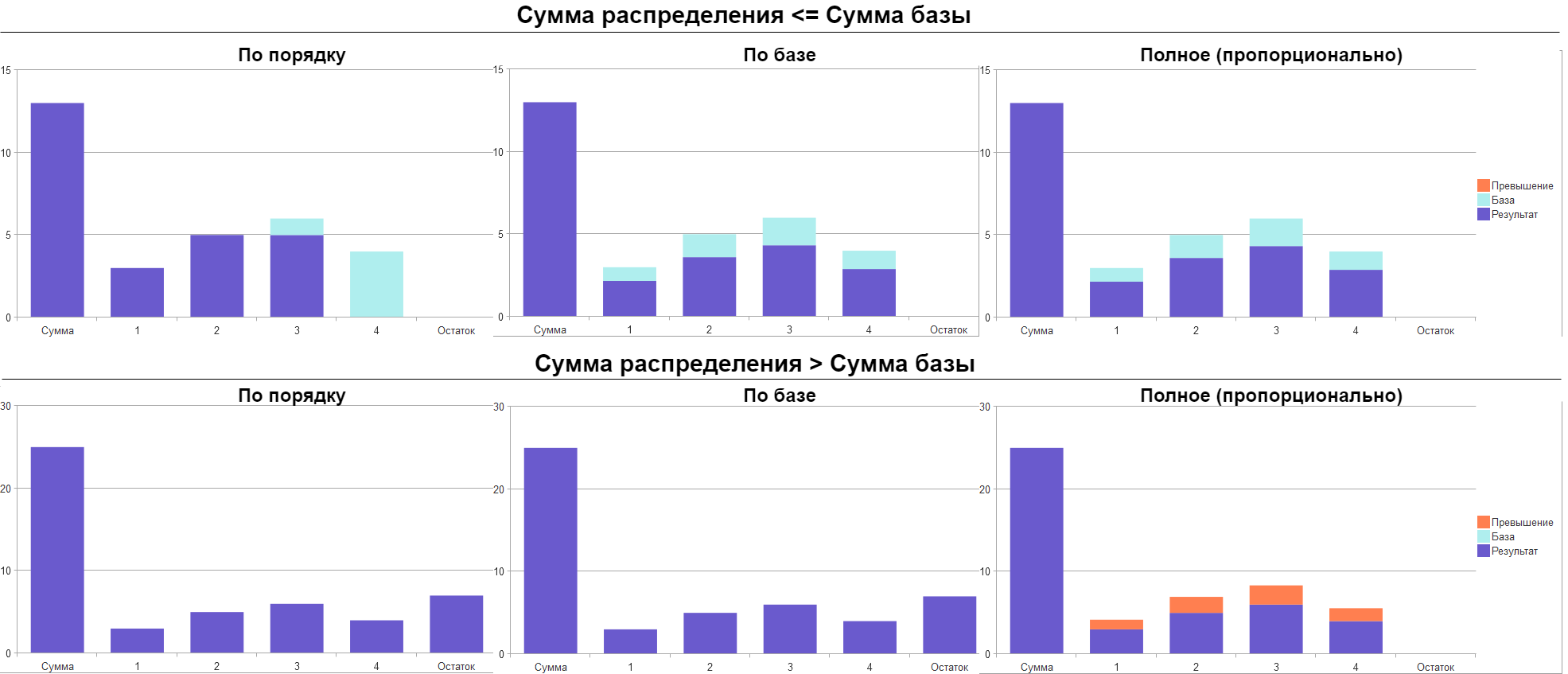
Варианты распределения
По порядку
Суть следующего распределения в подборе сумм из базовых коэффициентов в заданном порядке. При таком виде распределения превышение результата над базовыми коэффициентами не допускается при любом соотношении сумм.
Такой вид распределения подходит для задач: списание лимитов, подбор партий, подбор накладных для возврата, зачет авансов.
По базе
Результат такого распределения получается пропорционально коэффициентам базы. Ни при каком соотношении сумм превышение над базовыми коэффициентами также не допускается.
Примеры использования: реклассификация, конвертация.
Полное
Если сумма распределения не ограничена базой, но находится в пропорциональной зависимости, то применяется полное распределение.
Пример использования: распределение затрат пропорционально площади.
Связь таблицы с базой
Отношение
Понятие отношения является важным элементом модели распределения. По сути это соединение таблицы распределения с базой через промежуточную таблицу. Отношение позволяет для одной строки таблицы предложить несколько вариантов базы.
Например заявка на расходование денежных средства должна разложиться по БДДС. В БДДС помимо бюджета по статьям расхода заложены также непредвиденные расходы. Если лимитов по статье заявки не хватает, то возможно они есть по статье непредвиденные расходы. В таком сценарии распределения требуется отношение, которое соединит каждую строку заявки с лимитами по статье расхода и с лимитами по статье непредвиденных расходов. При этом приоритет непредвиденных расходов будет ниже, чем по указанной статье из заявки.
Другой пример. Заявка на расходование средств проходит по программе финансирования. Есть соответствие между статьями БДДС и бюджета финансирования. Это соответствие описывается через отношение статей БДДС и статей финансового бюджета.
Еще один пример. Заявка распределена по бюджету финансирования по статьям. На этапе проведения списания по выписке движения детализируются до уровня очереди кредитной линии, где каждая статья бюджета финансирования разложена по номерам очередей.
В первых двух примерах отношения не уникальны, т.к. для разных строк таблицы распределения может быть определена одна строка базы распределения (статья непредвиденные расходы, статья бюджета финансирования). В последнем примере проиходит уточнение и оно уже однозначное. В этом случае будет уникальное отношение.
Построение отношения
Существует практически универсальный подход к построению таблицы отношения. По сути это объединение запросов по порядку применения отношений: 1-ый приоритет, 2-й и т.д. Для каждого запроса объединения необходимо соединить измерения таблицы и значения измерений базы.
В рассмотренном примере разложения заявки по статьям БДДС отношение будет состоять из 2-х запросов: по статьям заявки и по статье непредвиденные расходы.
Конструирование таблицы отношения
;// ЗАПРОС ПАКЕТА. ВТ_ОТНОШЕНИЕ
МодельЗапроса.ЗапросПакета().Поместить("ВТ_ОТНОШЕНИЕ")
.Выбрать()
.Источник("ВТ_ТАБЛИЦА")
.Источник("ВТ_БАЗА")
.ВнутреннееСоединение("ВТ_ТАБЛИЦА", "ВТ_БАЗА")
.Связь("Статья")
.Поле("1", "Порядок")
.Поле("ВТ_ТАБЛИЦА.Статья", "СтатьяТаблица")
.Поле("ВТ_БАЗА.Статья", "СтатьяБаза")
.ОбъединитьВсе()
.Источник("ВТ_ТАБЛИЦА")
.Поле("2", "Порядок")
.Поле("ВТ_ТАБЛИЦА.Статья", "СтатьяТаблица")
.Поле("&СтатьяНепредвиденныеРасходы", "СтатьяБаза")
;
Если же имеет место распределение вначале по статьям в заявке, указанных в списании, затем по всем оставшимся статьям, которые не расшифрованы (указана общая сумма без детализации), то в таком случае у нас получается отношение с разным количеством связей. 1-й приоритет - связь по статье и заявке, 2-й приоритет - связь только по заявке (по всем оставшимся статьям). Такое отношение можно смоделировать, если убрать связь таблицы и базы (перемножение вариантов).
Конструирование таблицы отношения с переменным количеством связей
;// ЗАПРОС ПАКЕТА. ВТ_ОТНОШЕНИЕ
МодельЗапроса.ЗапросПакета().Поместить("ВТ_ОТНОШЕНИЕ")
.Выбрать()
.Источник("ВТ_ТАБЛИЦА")
.Источник("ВТ_БАЗА")
.ВнутреннееСоединение("ВТ_ТАБЛИЦА", "ВТ_БАЗА")
.Связь("Статья")
.Поле("1", "Порядок")
.Поле("ВТ_ТАБЛИЦА.Статья", "СтатьяТаблица")
.Поле("ВТ_БАЗА.Статья", "СтатьяБаза")
.ОбъединитьВсе()
.Источник("ВТ_ТАБЛИЦА")
.Источник("ВТ_БАЗА")
.Поле("2", "Порядок")
.Поле("ВТ_ТАБЛИЦА.Статья", "СтатьяТаблица")
.Поле("ВТ_БАЗА.Статья", "СтатьяБаза")
;
В общем задача построения отношения вполне решается на формальном уровне. Осталось только придумать как это можно описать в модели распределения в будущих версиях.
Переопределение результата
Задача переопределения результата формально выглядит так:
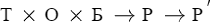
, где Т - таблица, О - отношение, Б - база, Р - результат, Р` - переопределенный результат
Если алгоритм распределения разложить на шаги i
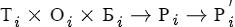
, то на каждом шаге распределения можно встроить свой алгоритм переопределения результата.
В примере "С ограничениме через отношение" для обычного распределения по порядку очереди весь результат будет соотнесен с 1-ой очередью. Если же ввести ограничение на распределение в 0.5, то результат` уже будет содержать распределение по 1-ой и 2-ой очередям:

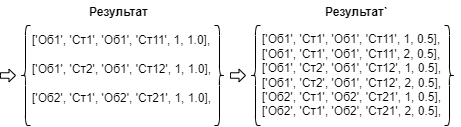
Пример "С ограничением через отношение"
Обычно результат распределения доступен после выполнения команды "Распределить":
// Подготовка данных
...
// Описание схемы модели распределения
...
МодельРаспределения.Распределить();
// Обработка результата распределения
...
Если же требуется переопределить результат, то вместо оператора "Распределить" необходимо использовать оператор "Следующий". После вызова этого оператора происходит вычисление очередного результата распределения и становятся доступными значения текущих данных итераторов: ИтераторТаблицы, ИтераторОтношения, ИтераторБазы.
Пример встраивания в алгоритм распределения ограничения по сумме
//МодельРаспределения.Распределить();// не используем!!!
Пока МодельРаспределения.Следующий() Цикл
...
// Доступные итераторы на шаге распределения
СтрокаТаблицы = МодельРаспределения.ИтераторТаблицы.ТекущиеДанные;
СтрокаОтношения = МодельРаспределения.ИтераторОтношения.ТекущиеДанные;// доступен только если есть отношение
СтрокаБазы = МодельРаспределения.ИтераторБазы.ТекущиеДанные;
// Строка результата на шаге распределения
СтрокаРезультата = МодельРаспределения.СтрокаРезультата;
// Переопределение результата распределения на шаге с учетом дополнительного ограничения
Если СтрокаРезультата.Сумма > 0.5 Тогда
СтрокаРезультата.Сумма = 0.5;
КонецЕсли;
...
КонецЦикла;
Конструктор модели распределения
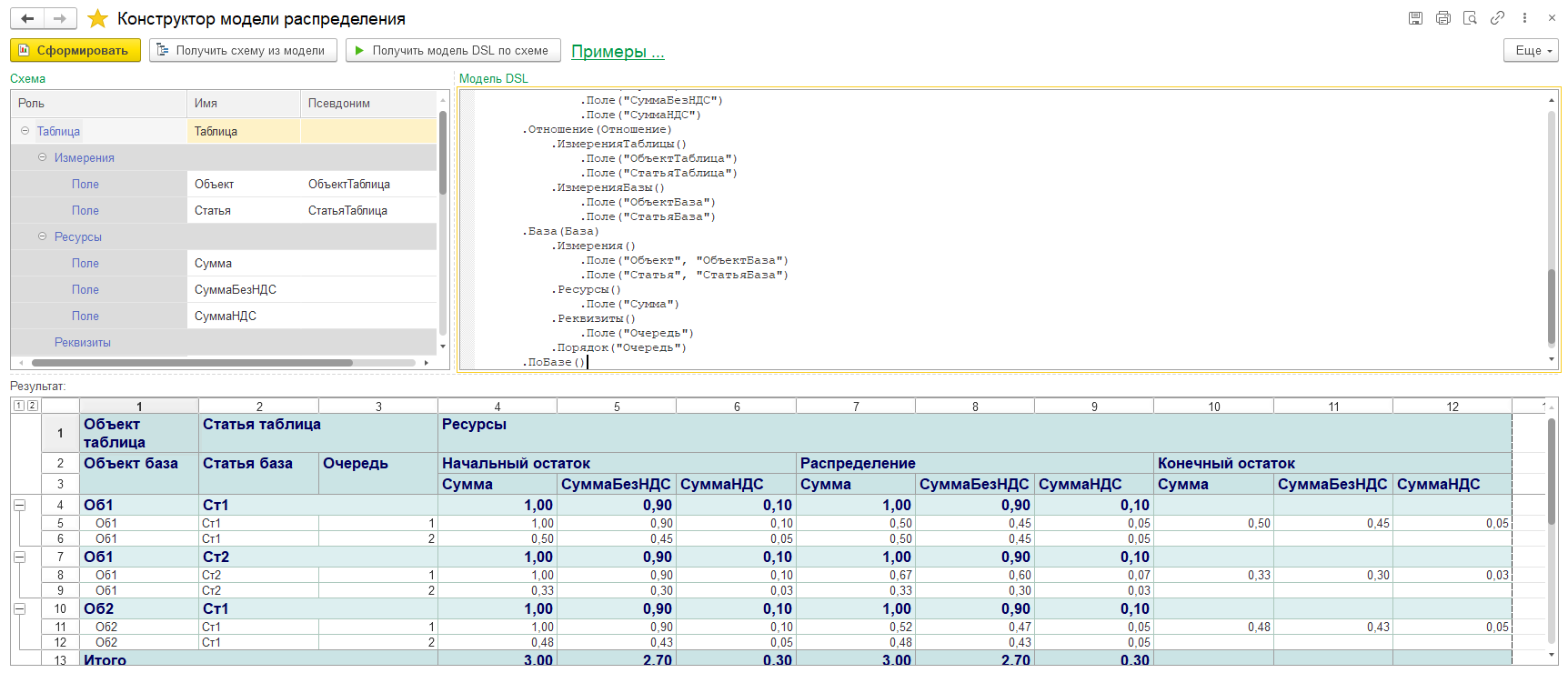
Интерфейс конструктора модели распределения
Конструктор выполняет следующие задачи: генерирует код модели DSL на основе визуального конструирования схемы, позволяет получить визуальное представление схемы из кода модели, формирует отчет по результату распределения из модели.
Для освоения конструктора предлагаю загрузить пример из меню "Примеры...". После загрузки примера выполните команду "Сформировать". Теперь у вас есть отчет по результату распределения и код модели. В коде модели есть также код инициирования таблицы распределения, отношения и базы.
Общий порядок работы с конструктором может быть таким:
- загрузить пример
- сформировать отчет по распределению
- проанализировать код модели и полученный результат по отчету
Код модели DSL состоит из разделов:
- Подготовка тестовых таблиц
- Модель DSL
Раздел "Подготовка тестовых таблиц"
Этот раздел нужен для моделирования распределения на данных. В разделе описываются таблицы модели:
- таблица распределения,
- таблица отношения (при необходимости),
- таблица базы распределения
Формат описания таблиц может быть любым: JSON, Таблица значений, Данные формы коллекция, имя временной таблицы. Все перечисленные типы допустимы для использования в модели DSL. Самый простой и наглядный вариант описания таблицы - в формате JSON. В реальном коде вы можете выбрать любой другой удобный тип из перечисленных выше.
Код модели DSL. Раздел "Тестовые таблицы"
///////////////////////////////////////////////////////////////////////
// Тестовые таблицы
///////////////////////////////////////////////////////////////////////
Таблица = "
|{
| 'Колонки': {'Объект': 'СТРОКА(50)', 'Статья': 'СТРОКА(50)', 'Сумма': 'ЧИСЛО(15, 2)', 'СуммаБезНДС': 'ЧИСЛО(15, 2)', 'СуммаНДС': 'ЧИСЛО(15, 2)'},
| 'Строки': [
| ['Ор2', 'Ко6', 5.31, 3.33, 1.98],
| ['Ор6', 'Ко9', 11.62, 6.28, 5.34],
| ['Ор2', 'Ко5', 11.78, 9.84, 1.94],
| ]
|}";
База = "
|{
| 'Колонки': {'Объект': 'СТРОКА(50)', 'Статья': 'СТРОКА(50)', 'Очередь': 'ЧИСЛО(1)', 'Сумма': 'ЧИСЛО(15, 2)'},
| 'Строки': [
| ['Ор2', 'Ко6', 1, 7.22],
| ['Ор1', 'Ко9', 2, 0.66],
| ['Ор3', 'Ко6', 3, 1.53],
| ]
|}";
Генератор тестовых данных
Генератор тестовых данных используется в команде "Получить модель DSL по схеме" для раздела "Подготовка тестовых данных".
Общий принцип генерируемых данных: все колонки таблиц - текстовые, ресурсы - числовые. Если используются доп. ресурсы, то генерируются значения доп. ресурсов, затем вычисляется значение основного ресурса как сумма по доп. ресурсам.
Тестовые таблицы, приведенные выше, получены с использованием генератора случайных данных. В примере исправлено:
- тип колонки "Очередь" со "СТРОКА(50)" на "ЧИСЛО(1)",
- значения колонки Очередь исправлены на числовые,
- значения измерений в первой строке базы приведены к значениям в первой строке таблицы - нужно чтобы таблица могла распределиться по базе
Если ручных исправлений не делать, то велика вероятность при проверке получить следующее сообщение:
Сообщение, свидетельствующее о том, что таблица не может быть распределена по базе
Раздел "Модель DSL"
Модель распределения представляет собой DSL для описания схемы распределения. Общая структура описания схемы на DSL:
- Таблица/Отношение/База
- Измерения/Ресурсы/Реквизиты
- Поле
- ...
- Порядок
- Измерения/Ресурсы/Реквизиты
- ПоБазе/ПоПорядку/Полное
Код модели DSL. Раздел "Модель DSL"
///////////////////////////////////////////////////////////////////////
// Модель DSL
///////////////////////////////////////////////////////////////////////
МодельРаспределения = Общий.МодельРаспределения()
.Таблица(Таблица)
.Измерения()
.Поле("Объект")
.Поле("Статья")
.Ресурсы()
.Поле("Сумма")
.Поле("СуммаБезНДС")
.Поле("СуммаНДС")
.База(База)
.Измерения()
.Поле("Объект")
.Поле("Статья")
.Ресурсы()
.Поле("Сумма")
.Реквизиты()
.Поле("Очередь")
;
Отчет по результату распределения
Отчет формируется следующим образом. В результат распределения добавляются колонки "Начальный остаток" и "Конечный остаток" для каждого из ресурсов. На каждом шаге распределения в добавленные колонки сохраняются значения ресурсов до распределения и после.
Полученная таблица распределения используется в качестве источника данных для отчета СКД. В отчет в поля группировок добавлены поля таблицы и базы распределения, а в качестве ресурсов - ресурсы из модели распределения. На выходе получается отчет по остаткам и оборотам из таблицы результата распределения.
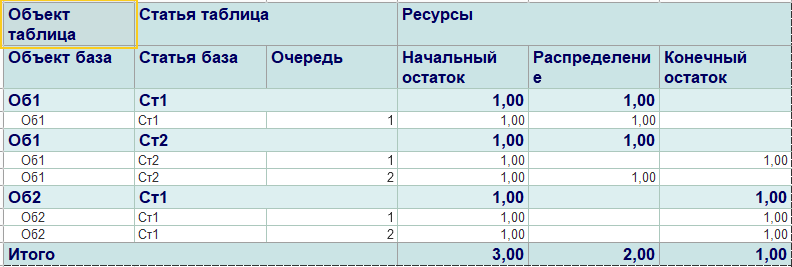
Отчет по результату распределения
Поставка
Разработка проекта ведется в EDT с использованием платформы 8.3.23.
Подсистемы: KASL.Модели.МодельРаспределения, KASLДемо._ДемоМодельРаспределения
Зависимости: БСП, Модель запроса, АТД массив.
"Конструктор" можно попробовать в демо базе в разделе "Библиотека подсистем КА". Демо обработку "Диаграмма распределения" можно найти в разделе "Библиотека подсистем КА Демо".
Проект выложен на github: distribution-model, distribution-model-constructor.
PS. Это продолжение темы Модель распределения суммы по базе.