Содержание
- В чем вопрос?
- Повысим ставки
- Расчет суммы кредита в консоли кода
- Подсчет итогов
- Математический подход
- Да здравствует ChatGPT!
- Сумма предела
- PS.
В чем вопрос?
Как-то ко мне обратилась жена со странным вопросом: как рассчитать сумму кредита такую, чтобы из него же и заплатить проценты за него? На первый взгляд это был абсурд, но моя жена кандидат экономических наук, и было бы недальновидно ее обвинять в глупости :).
Ок, подумал я, попробую помоделировать. Допустим, мы хотим взять кредит 100 рублей под 10% годовых в банке Б1, затем возьмем кредит на проценты 10 рублей у банка Б2, затем в банке Б3 возьмем кредит на 1 рубль и заплатим ему 10 копеек :)). Т.е. получается берем кредит на общую сумму 111 рублей, платим 10 копеек за проценты и радуемся жизни! Эврика, моя жена взломала систему! :))
Повысим ставки
Что-то я мелочусь так? Хочу взять 1 млн и не платить проценты по нему. Считать столбиком мне уже лень, составлю программу. Программу буду писать на Пи... - ой, нет, я люблю 1С.
Наверное, здесь нужна рекурсия. Что-то типа: Сумма кредита => Сумма процентов в банке Б1; Cумма кредита = Cумма процентов Б1 => Cумма процентов в банке Б2 и т.д.
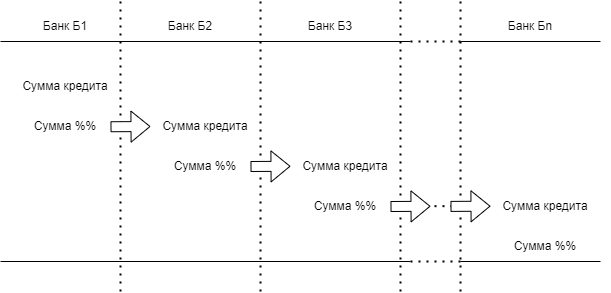
Писать буду в консоли кода. Обычно рекурсия подразумевает вызов функции из той же функции. Использование функций в консоли проблематично. Однако любую рекурсию также можно представить в виде цикла с аккумулятором. По сути рекурсивный вызов использует в качестве аккумулятора данные стека, а в цикле эту роль может выполнять обычный массив.
Расчет суммы кредита в консоли кода
Реализация алгоритма:
// Исходные данные
СуммаКредитаНачальная = 1000000;
Процент = 0.1;
// Инициализация рекурсии
СуммаКредита = СуммаКредитаНачальная;
МассивРезультатов = Новый Массив;
// Рекурсия в цикле
Для й = 1 По 100 Цикл
СуммаПроцентов = Окр(Процент * СуммаКредита, 2);
Если СуммаПроцентов = 0 Тогда
Прервать;
КонецЕсли;
МассивРезультатов.Добавить(Новый Структура("СуммаКредита, Процент, СуммаПроцентов", СуммаКредита, Процент, СуммаПроцентов));
СуммаКредита = СуммаПроцентов;
КонецЦикла;
Вывести результат можно в виде JSON. Я использую для этого собственную функцию, Вы можете скачать одну из моих демо баз и запустить в ней консоль, либо используйте собственный вариант.
Сообщить(ОбщийКлиентСервер.ОбъектВJSON(МассивРезультатов));
Результат:
[
{
"СуммаКредита": 1000000,
"Процент": 0.1,
"СуммаПроцентов": 100000
},
{
"СуммаКредита": 100000,
"Процент": 0.1,
"СуммаПроцентов": 10000
},
{
"СуммаКредита": 10000,
"Процент": 0.1,
"СуммаПроцентов": 1000
},
{
"СуммаКредита": 1000,
"Процент": 0.1,
"СуммаПроцентов": 100
},
{
"СуммаКредита": 100,
"Процент": 0.1,
"СуммаПроцентов": 10
},
{
"СуммаКредита": 10,
"Процент": 0.1,
"СуммаПроцентов": 1
},
{
"СуммаКредита": 1,
"Процент": 0.1,
"СуммаПроцентов": 0.1
},
{
"СуммаКредита": 0.1,
"Процент": 0.1,
"СуммаПроцентов": 0.01
}
]
Из результата видно, что для кредита в 1 млн рублей достаточно получить кредит в восьми банках и проценты платить не нужно!
Подсчет итогов
Давайте разбираться дальше. А что получается с итоговыми суммами: сумма кредита, сумма процентов? Уж извините, но я воспользуюсь возможностями абстрактного массива для подсчета сумм:
СуммаПроцентов = РаботаСМассивом.АТДМассив(МассивРезультатов)
.Отобразить("Элемент.СуммаПроцентов")
.Преобразовать("Накопитель + Элемент", 0, 0)
;
СуммаКредита = РаботаСМассивом.АТДМассив(МассивРезультатов)
.Отобразить("Элемент.СуммаКредита")
.Преобразовать("Накопитель + Элемент", 0, 0)
;
ЭффективныйПроцент = Окр(СуммаПроцентов / СуммаКредитаНачальная, 3);
Результат:
Шагов: 8, Сумма кредита: 1 111 111.1, Сумма процентов: 111 111.11, Эффективный процент: 0.111
По результату процент по кредиту стал больше. Ну и ладно, зато проценты платить не нужно.

Математический подход
"Все эти алгоритмы оставь себе, а мне нужна формула" - жена не оценила моего предыдущего подвига :).
Что ж, давайте порассуждаем индуктивно. Чтобы посчитать сумму процентов, нужно просуммировать суммы процентов по каждому кредиту всех банков:
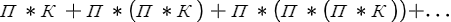
, где П - процент, К - кредит. Перепишем математически:
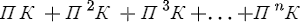
На вид это степенной ряд. Показательная функция на графике выглядит вполне себе сходимой:
Математику я люблю, но мозги уже не те...
Да здравствует ChatGPT!
Я> выведи предел бесконечного ряда: a + a^2 + a^3 + a^4 и т.д., где 2, 3, 4 - это x
ChatGPT> Чтобы найти предел бесконечного ряда a + a^2 + a^3 + a^4 + ... , где 2, 3, 4 и так далее - это значения переменной x, нам следует рассмотреть два случая в зависимости от значения основания "a":
1. Если основание "a" больше единицы (a > 1), то для нахождения предела ряда мы можем использовать формулу суммы бесконечно убывающей геометрической прогрессии. Формула для суммы такой прогрессии имеет вид:
S = a / (1 - a),
где S - сумма прогрессии, а "a" - основание прогрессии. Однако, для того чтобы эта формула была применима, требуется условие 0 < a < 1. Иначе говоря, основание "a" должно быть в интервале между 0 и 1.
2. Если основание "a" меньше единицы (a < 1), то ряд будет сходиться к определенному значению в зависимости от значения "a" и переменной "x". В этом случае мы можем найти предел ряда аналитически, используя формулу для суммы геометрической прогрессии:
S = a / (1 - a),
где S - сумма ряда.
Важно отметить, что для обоих случаев предел будет существовать только при выполнении условия 0 < a < 1. В противном случае, ряд будет расходиться или иметь неконечное значение.
Чартжпт - сила! А если так:
Я> выведи предел бесконечного ряда: a*b + a^2*b + a^3*b + a^4*b и т.д., где 2, 3, 4 - это x
ChatGPT> Для нахождения предела бесконечного ряда a*b + a^2*b + a^3*b + a^4*b + ... , где 2, 3, 4 и так далее - это значения переменной x, мы можем применить формулу суммы бесконечно убывающей геометрической прогрессии.
В данном случае, каждый элемент ряда имеет вид a^x * b, где "a" - это основание, а "b" - это постоянный множитель.
Формула для суммы бесконечного ряда геометрической прогрессии, где |a| < 1, имеет вид:
S = a*b / (1 - a),
где S - сумма ряда.
Таким образом, предел этого бесконечного ряда будет равен a*b / (1 - a), при условии, что |a| < 1. Если условие не выполнено (то есть |a| >= 1), то ряд будет расходиться или иметь неконечное значение.
А как докажешь?
Я> выведи по шагам сумму предела
ChatGPT> Хорошо, выведем пошагово сумму предела бесконечного ряда a + a^2 + a^3 + a^4 + ...
Для начала, обозначим сумму данного ряда как S. То есть,
S = a + a^2 + a^3 + a^4 + ...
Затем умножим обе части уравнения на a:
aS = a^2 + a^3 + a^4 + a^5 + ...
Вычтем это новое уравнение из первого:
S - aS = a
S(1 - a) = a
Получили уравнение:
S = a / (1 - a)
Таким образом, получили сумму S предела бесконечного ряда:
S = a / (1 - a)
Это является явной формулой для суммы данного ряда. Обратите внимание, что данная формула справедлива только при условии, что |a| < 1.
Ну просто прелесть, вкалывают роботы! :)
Сумма предела
Итого наша формула предела будет выглядеть так:

В моем случае это будет:
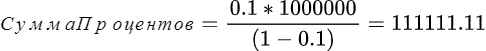
Итого нужно взять 1 111 111.11 рублей и, не платя процентов, пользоваться весь год 1 млн рублей.
PS.
Конечно, чудес в реальной жизни не бывает и за все нужно платить. Вот что думает по этому поводу ИИ:
Я> если взять кредит, а на проценты взять еще кредит и еще, то при одинаковой процентной ставке сумма уплаты стремится к нулю. В чем здесь подвох?
ChatGPT> Подобная стратегия брать кредиты для покрытия процентов по другим кредитам является примером пирамиды долгов, которая теоретически может показаться выгодной, но на практике несет серьезные риски.
Основной подвох заключается в том, что когда вы берете новый кредит для погашения процентов по предыдущему, ваш общий долг только увеличивается. В конечном итоге, вы оказываетесь в ситуации, когда нужно погашать все больше и больше долга за счет новых кредитов, и всё это при одинаковой процентной ставке.
Помимо этого, банки и кредитные организации часто взимают дополнительные комиссии и условия при предоставлении кредитов, так что вам придется не только вернуть основной долг, но и оплатить эти дополнительные расходы.
Еще одним риском является возможность возникновения финансовых трудностей. В случае, если у вас не будет достаточных средств для погашения кредитов, вы можете оказаться в серьезном долговом кризисе, который может негативно сказаться на вашей финансовой стабильности и иметь долгосрочные последствия.
Всегда рекомендуется рассматривать взятие кредитов с осторожностью и ответственностью. Лучше всего учитывать свои возможности и способности, чтобы на долгосрочной основе не находиться в ситуации, где вы столкнетесь с нестабильностью и растущими долгами.
Я> но таким образом можно добиться того, что проценты будут оплачены участниками пирамиды, а платить придется только тело кредита
ChatGPT> Хотя на первый взгляд может показаться, что такая стратегия позволяет оплатить только тело кредита с помощью процентов, оплачиваемых другими кредитами, на самом деле это неправильное предположение. Здесь следует учитывать несколько важных факторов:
1. Неограниченное усложнение: Предположим, вы продолжаете брать новые кредиты, чтобы покрыть проценты по предыдущим. Эта стратегия имеет неограниченный потенциал усложнения. В конечном итоге вы можете столкнуться с огромным количеством кредитов и невозможностью покрыть все проценты, что приведет к финансовому краху.
2. Платежи и комиссии: При каждом новом кредите, который вы берете, банки и кредитные организации взимают платежи и комиссии. Эти дополнительные расходы будут накапливаться, и в конечном итоге вы окажетесь в долгу больше, чем при начале этой стратегии.
3. Кредитная история: Если вы не в состоянии своевременно выплачивать кредиты или надолго оказываетесь в долгу, это может серьезно повлиять на вашу кредитную историю. В результате вы можете столкнуться с проблемами при получении будущих кредитов или с более высокой процентной ставкой.
4. Юридические последствия: Использование обманных стратегий погашения кредитов может нарушать законы и правила финансового регулирования. Если вы будете пойманы в таком мошенничестве, это может привести к юридическим последствиям, штрафам или даже уголовной ответственности.
В итоге, подобная пирамида долгов является неправомерной и непредсказуемой стратегией, которая может серьезно навредить вашей финансовой стабильности и иметь долгосрочные негативные последствия. Рекомендуется всегда быть ответственным заемщиком, соблюдать условия кредитных договоров и избегать подобных манипуляций.
В общем, не смог я выудить у ИИ, в чем здесь подвох. И тут уж, извините, пришлось своим умом доходить, чего и Вам желаю!
Спасибо, что дочитали :)
Вступайте в нашу телеграмм-группу Инфостарт