Представим себе ситуацию, в которой аналитик данных, вооруженный знаниями эконометрии и инструментом в виде платформы 1С:Предприятие, сталкивается с задачей построения модели, описывающей зависимость некоторой целевой переменной от нескольких факторов. Целевая переменная может представлять собой, например, объем продаж, количество клиентов или любой другой показатель, изменение которого необходимо прогнозировать и контролировать. В качестве факторов могут выступать различные экономические индикаторы, маркетинговые активности, сезонные колебания или другие переменные, которые, предположительно, влияют на целевую переменную.
Первоначальная стадия работы заключается в сборе и подготовке данных. Аналитик формирует массивы данных, содержащие значения целевой переменной и соответствующих факторов за определенный период времени. Важно отметить, что данные должны быть очищены от выбросов и пропусков, а также приведены к единому формату для обеспечения корректности дальнейшего анализа. Этот этап требует внимательности и аккуратности, поскольку ошибки в данных могут существенно повлиять на результаты моделирования.
Затем наступает этап выбора подходящей эконометрической модели. В данном случае, речь идет о множественной регрессии, которая позволяет оценить влияние нескольких факторов на целевую переменную одновременно. Однако, прежде чем применять эту модель, необходимо убедиться в выполнении ряда предпосылок, таких как линейность связи между переменными, отсутствие мультиколлинеарности (сильной корреляции между факторами) и гомоскедастичность (постоянство дисперсии ошибок). Нарушение этих предпосылок может привести к смещенным и неэффективным оценкам.
Чтобы учесть возможную нелинейность связей, аналитик решает включить в модель не только сами факторы, но и их квадраты. Это позволяет захватить эффекты, когда влияние фактора на целевую переменную меняется с ростом его значения. Например, если речь идет о маркетинговых инвестициях, то на начальном этапе увеличение инвестиций может приводить к значительному росту продаж, но затем, по мере насыщения рынка, отдача от инвестиций может снижаться. Включение квадратичного члена позволяет учесть этот эффект убывающей отдачи.
После выбора модели наступает этап оценки ее параметров. Аналитик использует функционал платформы 1С:Предприятие для вычисления коэффициентов регрессии, которые показывают силу и направление влияния каждого фактора на целевую переменную. Важным элементом оценки является проверка статистической значимости коэффициентов. Для этого используются p-значения, которые показывают вероятность того, что наблюдаемый эффект является случайным. Если p-значение меньше определенного уровня значимости (обычно 0.05 или 0.1), то коэффициент считается статистически значимым, и можно сделать вывод о наличии реальной связи между фактором и целевой переменной.
Помимо оценки значимости отдельных коэффициентов, необходимо оценить общее качество модели. Для оценки качества модели используется R-квадрат, который показывает, какую долю общей изменчивости (дисперсии) целевой переменной объясняет модель. Чем ближе R-квадрат к 1, тем лучше модель соответствует данным. Однако, следует учитывать, что R-квадрат имеет тенденцию увеличиваться при добавлении в модель новых факторов, даже если эти факторы слабо связаны с целевой переменной. Для учета этого эффекта и предотвращения переобучения модели используется скорректированный R-квадрат, который учитывает количество факторов в модели и штрафует за излишнюю сложность.
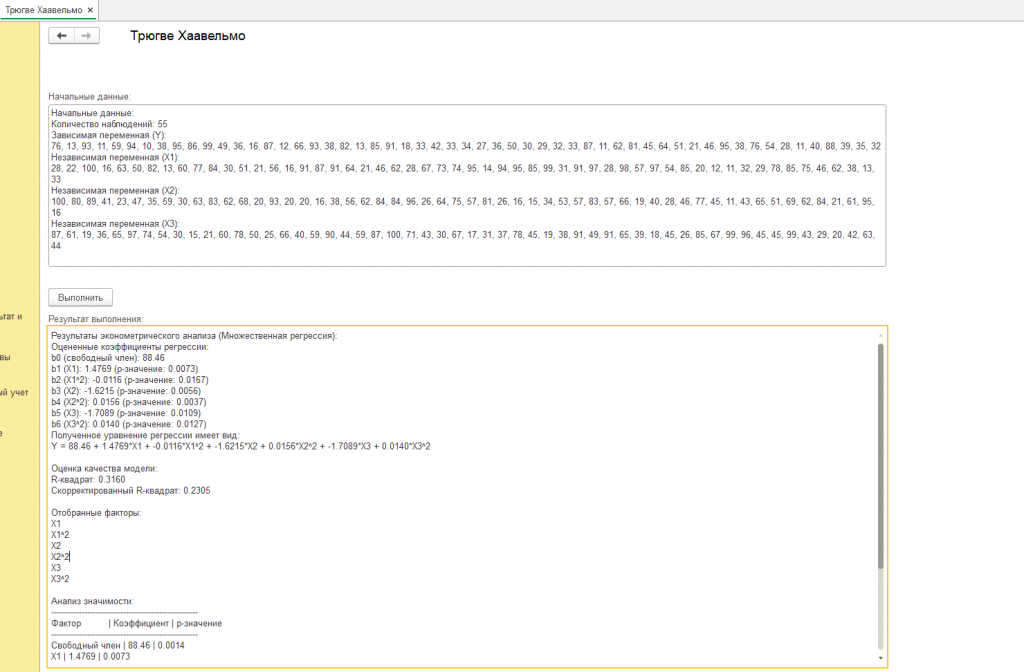
Предположим, что после проведения эконометрического анализа аналитик получает следующие результаты. Модель включает в себя три фактора (X1, X2, X3), а также их квадраты. Все факторы оказываются статистически значимыми на уровне 5%, а R-квадрат составляет 0.3160. Это означает, что модель объясняет около 32% дисперсии целевой переменной.
На первый взгляд, такой R-квадрат может показаться не очень высоким. Однако, важно учитывать, что в реальных экономических задачах достижение высокого R-квадрата не всегда возможно и не всегда является самоцелью. Главное, чтобы модель была полезна для принятия управленческих решений. В данном случае, модель позволяет оценить влияние каждого фактора на целевую переменную и прогнозировать ее изменение при изменении значений факторов.
Анализируя коэффициенты регрессии, аналитик может выявить, какие факторы оказывают наибольшее влияние на целевую переменную, а какие – наименьшее. Он также может определить, является ли влияние факторов положительным или отрицательным. Эта информация может быть использована для разработки стратегий по управлению целевой переменной.
Например, если фактор X1 оказывает положительное влияние на продажи, то можно рассмотреть возможность увеличения инвестиций в этот фактор. С другой стороны, если фактор X2 оказывает отрицательное влияние, то необходимо выяснить причины этого влияния и принять меры по его нейтрализации.
Включение квадратичных членов в модель позволяет выявить нелинейные эффекты. Например, если коэффициент при квадрате фактора X1 является отрицательным, то это означает, что влияние X1 на целевую переменную снижается с ростом X1. Это может указывать на наличие эффекта убывающей отдачи.
Важно помнить, что построенная модель является лишь упрощенным представлением реальности. Она не может учесть все факторы, влияющие на целевую переменную. Поэтому, результаты моделирования необходимо интерпретировать с осторожностью и учитывать контекст конкретной ситуации.
Аналитик должен постоянно следить за изменениями в окружающей среде и корректировать модель при необходимости. Он также должен использовать другие инструменты анализа, такие как визуализация данных и экспертные оценки, для получения более полной картины.
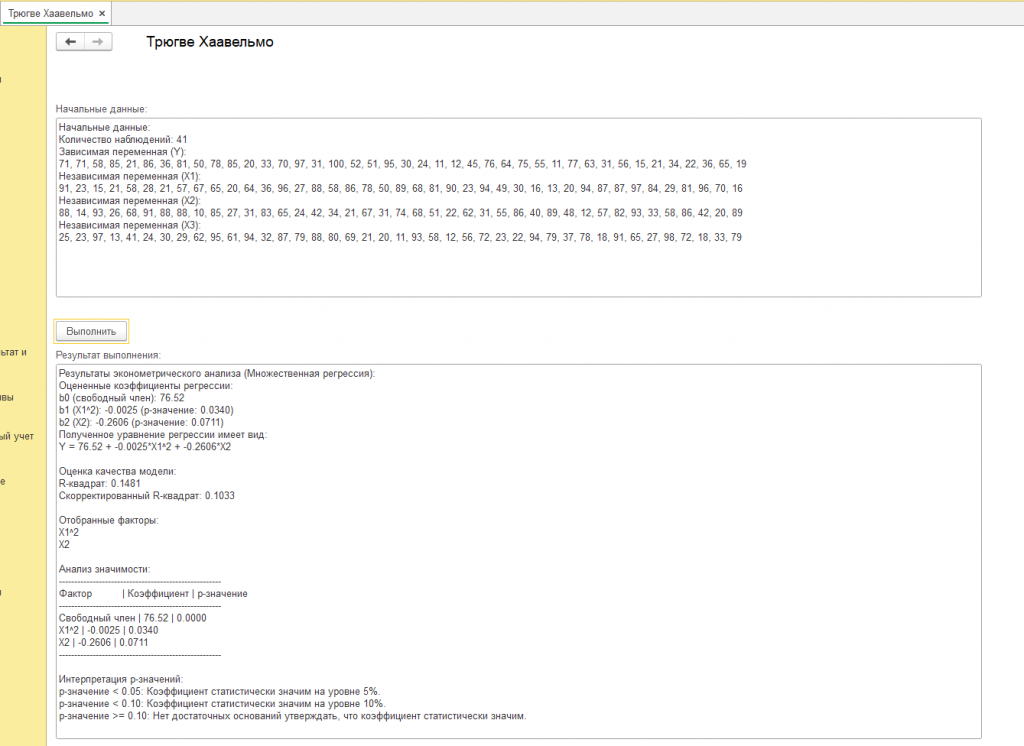
Рассмотрим второй пример, "результат" написанной обработки 1с 8.3 с начальными данными сгенерированными случайными числами для "Трюгве Хаавельмо" (см. скриншот с подписью "пример 2").

Итак, давайте разберем полученные результаты простым языком, без сложных терминов. Представьте, что мы пытаемся понять, что влияет на некоторую величину "Y", например, на продажи мороженого. У нас есть три фактора: "X1", "X2" и "X3" (например, температура воздуха, количество рекламы и день недели). Мы собрали данные и построили математическую модель, чтобы выяснить, как эти факторы влияют на "Y".
Наша модель показывает, что величина "Y" в среднем равна 75.91, когда факторы "X1", "X2" и "X3" равны нулю. Но, конечно, факторы редко бывают нулевыми, поэтому посмотрим, как они меняют эту величину.
Фактор "X1" влияет на "Y" не напрямую, а через свой квадрат ("X1 в квадрате"). Это означает, что влияние "X1" на "Y" нелинейное, то есть меняется по мере увеличения "X1". Коэффициент при "X1 в квадрате" равен 0.0023. Это небольшое положительное число. Можно представить, что небольшое изменение "X1" почти не влияет на "Y", но с ростом "X1" влияние становится более заметным. Важно, что мы достаточно уверены в этом влиянии, так как "p-значение" равно 0.0381, что меньше 0.05. Это означает, что с большой вероятностью эта связь реальна, а не случайна.
Фактор "X2" напрямую влияет на "Y". Коэффициент равен -1.2198. Это означает, что с ростом "X2" величина "Y" уменьшается. Но здесь уверенность чуть меньше, так как "p-значение" равно 0.0664, что больше 0.05, но меньше 0.10. Это говорит о том, что влияние "X2" на "Y" скорее всего есть, но мы не можем быть уверены в этом на 100%. Возможно, это влияние случайно.
Интересно, что на "Y" влияет не только "X2", но и его квадрат ("X2 в квадрате"). Коэффициент при "X2 в квадрате" равен 0.0108. Это положительное число, которое компенсирует отрицательное влияние "X2" на больших значениях. Это означает, что на маленьких значениях "X2" увеличение "X2" уменьшает "Y", но на больших значениях увеличение "X2" начинает увеличивать "Y". Точно так же, как и с "X2" уверенности в влиянии не много, так как "p-значение" равно 0.0701.
Теперь о том, насколько хорошо наша модель описывает реальность. Есть такая штука, как "R-квадрат", которая показывает, какую часть изменений "Y" объясняют наши факторы. В нашем случае "R-квадрат" равен 0.1285. Это означает, что наша модель объясняет только около 13% изменений "Y". Это очень мало! Можно сказать, что наша модель не очень хорошо описывает то, что происходит на самом деле.
Еще одна штука - "Скорректированный R-квадрат", который учитывает количество факторов в нашей модели. Он равен 0.0762, что еще меньше, чем "R-квадрат". Это говорит о том, что добавление факторов не сильно улучшило модель.
Что делать дальше? Самое главное - не полагаться на эту модель для принятия решений, так как значения массивов заполнены генератором случайных чисел. Она слишком плохо описывает реальность. Нужно искать другие факторы, которые влияют на "Y", или использовать другие методы построения модели.
А теперь перейдем к теории, если было непонятно.
Вероятностная революция в эконометрике: Наследие Трюгве Хаавельмо
Трюгве Хаавельмо, выдающийся норвежский экономист и лауреат Нобелевской премии по экономике 1989 года, оставил неизгладимый след в развитии эконометрики, совершив подлинную революцию в методологии экономического анализа. Его вклад выходит далеко за рамки простого применения статистических методов к экономическим данным; он заключался в фундаментальном переосмыслении самой природы экономических связей и введении вероятностного подхода, который позволил эконометрике стать полноценной научной дисциплиной. До Хаавельмо, эконометрика часто рассматривалась как набор инструментов для подтверждения или опровержения заранее сформулированных экономических теорий, а акцент делался на детерминированных моделях, которые не учитывали неизбежную неопределенность и случайность, присущие экономическим явлениям. Хаавельмо же предложил рассматривать экономические модели как вероятностные конструкции, отражающие не точные законы, а скорее тенденции и вероятности, управляющие поведением экономических агентов. Этот сдвиг парадигмы имел далеко идущие последствия для методологии, практики и интерпретации эконометрических исследований.
Одним из ключевых положений, выдвинутых Хаавельмо, является необходимость четкого разграничения между теоретическими моделями и эмпирическими данными. Он утверждал, что экономические теории, как правило, являются упрощенными представлениями реальности, основанными на определенных предположениях и абстракциях. Эмпирические данные, напротив, отражают сложную и многогранную реальность, в которой действует множество факторов, не всегда учитываемых в теоретических моделях. Задача эконометрики, по мнению Хаавельмо, состоит в том, чтобы установить связь между этими двумя мирами – между упрощенными теоретическими конструкциями и сложной эмпирической реальностью. Эта связь должна быть установлена с помощью вероятностных методов, которые позволяют учитывать неопределенность и случайность, присущие экономическим данным. Вместо того, чтобы стремиться к точному соответствию между теорией и данными, эконометрика должна оценивать вероятность того, что наблюдаемые данные согласуются с предсказаниями теоретической модели. Такой подход позволяет избежать ложных выводов и более реалистично оценивать применимость экономических теорий.
Хаавельмо подчеркивал важность построения экономических моделей на основе четких и явных предпосылок. Он критиковал практику использования ad hoc моделей, которые строились без достаточного теоретического обоснования и которые часто приводили к противоречивым и ненадежным результатам. По его мнению, экономические модели должны быть основаны на строгих аксиомах и принципах, которые отражают фундаментальные законы экономики. Эти аксиомы должны быть четко сформулированы и явно указаны в модели. Только в этом случае можно будет оценить адекватность модели и интерпретировать ее результаты. Кроме того, Хаавельмо отмечал, что предпосылки модели должны быть реалистичными и соответствовать наблюдаемым экономическим данным. Если предпосылки модели сильно противоречат реальности, то результаты моделирования будут ненадежными и бесполезными.
Вклад Хаавельмо в развитие теории идентификации также имеет огромное значение для эконометрики. Проблема идентификации возникает, когда невозможно однозначно оценить параметры экономической модели на основе имеющихся данных. Это может происходить, например, когда существует несколько различных моделей, которые одинаково хорошо согласуются с данными. В этом случае невозможно определить, какая из моделей является правильной. Хаавельмо разработал ряд методов, позволяющих определить, является ли модель идентифицируемой, и если да, то как правильно оценить ее параметры. Его работы в этой области стали основой для дальнейших исследований в теории идентификации и оказали значительное влияние на практику эконометрического моделирования.
Важно отметить, что работа Хаавельмо оказала влияние не только на эконометрику, но и на экономическую науку в целом. Его идеи о вероятностной природе экономических связей и о необходимости четкого разграничения между теорией и данными стали общепризнанными и широко используются в экономических исследованиях. Он также подчеркивал важность использования математических методов для формализации экономических теорий и для анализа экономических данных. Его работы способствовали повышению научного уровня экономических исследований и внесли значительный вклад в развитие экономической науки.
Развитие теории идентификации: От Хаавельмо к современным вызовам
Теория идентификации, фундамент которой заложил Трюгве Хаавельмо, является краеугольным камнем современной эконометрики. Она решает принципиальный вопрос: можно ли вообще, имея определенный набор данных и модель, однозначно оценить параметры этой модели? Если модель не идентифицируема, то никакое количество данных не позволит нам получить надежные оценки, что делает дальнейший анализ бессмысленным. Хаавельмо, осознавая эту фундаментальную проблему, разработал первые систематические методы для определения идентифицируемости моделей. Его работы стали отправной точкой для обширных исследований, которые продолжаются и в настоящее время, решая все более сложные задачи, возникающие в современной эконометрике. Развитие теории идентификации тесно связано с эволюцией экономических моделей и доступностью данных. По мере усложнения моделей и увеличения объема доступных данных, возникают новые проблемы идентификации, требующие новых подходов и методов.
Одним из важнейших достижений в теории идентификации после Хаавельмо стало развитие методов идентификации структурных моделей. Структурные модели, в отличие от редуцированных форм, стремятся отразить причинно-следственные связи между экономическими переменными. Они основаны на экономических теориях и описывают поведение экономических агентов, а также технологические и институциональные ограничения. Идентификация структурных моделей является более сложной задачей, чем идентификация редуцированных форм, поскольку требует учета эндогенности переменных. Эндогенность возникает, когда одна или несколько переменных в модели одновременно определяются другими переменными в модели. В этом случае обычные методы оценки, такие как метод наименьших квадратов, дают смещенные и несостоятельные результаты. Для решения проблемы эндогенности используются различные методы, такие как метод инструментальных переменных, метод максимального правдоподобия и метод обобщенных моментов.
Важным направлением исследований в теории идентификации является разработка методов идентификации моделей с нелинейными ограничениями. Нелинейные ограничения возникают, когда параметры модели связаны между собой нелинейными уравнениями. Такие ограничения часто встречаются в моделях, основанных на экономических теориях, таких как теория рациональных ожиданий и теория динамической оптимизации. Идентификация моделей с нелинейными ограничениями является сложной задачей, поскольку требует использования численных методов и сложных алгоритмов оптимизации. Однако, прогресс в вычислительной технике и разработка новых алгоритмов позволили значительно продвинуться в этой области.
Современная эконометрика также сталкивается с проблемой идентификации в условиях высокой размерности. Высокая размерность возникает, когда количество переменных в модели превышает количество наблюдений. В этом случае обычные методы оценки становятся неэффективными, поскольку приводят к переобучению модели. Переобучение означает, что модель хорошо описывает имеющиеся данные, но плохо прогнозирует новые данные. Для решения проблемы высокой размерности используются различные методы регуляризации, такие как L1-регуляризация (lasso) и L2-регуляризация (ridge regression). Эти методы добавляют штраф к функции потерь, который ограничивает сложность модели и предотвращает переобучение.
Развитие теории идентификации также связано с появлением новых типов данных, таких как данные панельных наблюдений и данные социальных сетей. Данные панельных наблюдений содержат информацию о нескольких экономических агентах (например, домохозяйствах или фирмах) за несколько периодов времени. Данные социальных сетей содержат информацию о взаимосвязях между экономическими агентами. Использование этих типов данных требует разработки новых методов идентификации, которые учитывают специфические особенности данных.
Вероятностный подход Хаавельмо и современная макроэконометрика: Моделирование ожиданий и неопределенности
Вероятностный подход, предложенный Трюгве Хаавельмо, оказал глубокое влияние на современную макроэконометрику, особенно в контексте моделирования ожиданий и неопределенности. Традиционные макроэкономические модели часто предполагали, что экономические агенты обладают совершенной информацией и рациональными ожиданиями, то есть их ожидания относительно будущего состояния экономики в точности соответствуют предсказаниям модели. Однако, такая предпосылка является нереалистичной и противоречит наблюдаемым данным. В реальном мире экономические агенты сталкиваются с неопределенностью и неполной информацией, и их ожидания часто оказываются ошибочными. Вероятностный подход Хаавельмо позволяет более реалистично моделировать ожидания и неопределенность, учитывая, что экономические агенты формируют свои ожидания на основе имеющейся у них информации и с учетом вероятности различных сценариев развития экономики.
Современная макроэконометрика использует различные методы для моделирования ожиданий и неопределенности. Одним из наиболее распространенных методов является использование моделей с рациональными ожиданиями, в которых экономические агенты формируют свои ожидания, используя всю доступную информацию и зная структуру модели. Однако, в отличие от традиционных моделей с рациональными ожиданиями, современные модели учитывают, что экономические агенты могут иметь ограниченные вычислительные возможности и не могут обрабатывать всю доступную информацию. Это приводит к тому, что их ожидания могут отклоняться от предсказаний модели. Для моделирования этих отклонений используются различные методы, такие как модели с обучающимися агентами и модели с ограниченной рациональностью.
Модели с обучающимися агентами предполагают, что экономические агенты формируют свои ожидания, используя адаптивные алгоритмы обучения. Эти алгоритмы позволяют им корректировать свои ожидания на основе прошлых ошибок. Со временем агенты могут научиться правильно предсказывать будущее состояние экономики, но этот процесс обучения может быть медленным и не всегда приводит к рациональным ожиданиям. Модели с ограниченной рациональностью, напротив, предполагают, что экономические агенты используют упрощенные правила принятия решений, которые не всегда приводят к оптимальным результатам. Эти правила могут быть основаны на интуиции, опыте или социальных нормах. Использование упрощенных правил позволяет агентам экономить на вычислительных затратах, но может приводить к систематическим ошибкам в их ожиданиях.
Другим важным направлением в современной макроэконометрике является моделирование неопределенности. Неопределенность может быть связана с различными факторами, такими как политические риски, технологические изменения и изменения в мировой экономике. Для моделирования неопределенности используются различные методы, такие как модели с марковскими переключениями и модели с байесовской неопределенностью. Модели с марковскими переключениями предполагают, что экономика может находиться в разных режимах, характеризующихся разными значениями параметров. Переход между режимами происходит случайным образом, и экономические агенты не знают заранее, в каком режиме находится экономика. Модели с байесовской неопределенностью предполагают, что экономические агенты имеют неопределенные знания о значениях параметров модели. Они формируют свои ожидания на основе распределения вероятностей, которое отражает их степень уверенности в значениях параметров.
Вероятностный подход Хаавельмо также оказал влияние на развитие методов оценки макроэкономических моделей. Традиционные методы оценки, такие как метод наименьших квадратов, часто дают ненадежные результаты при применении к макроэкономическим данным. Это связано с тем, что макроэкономические данные часто характеризуются высокой степенью автокорреляции и гетероскедастичности. Для решения этих проблем используются различные методы, такие как метод обобщенных моментов и байесовские методы оценки. Метод обобщенных моментов позволяет оценить параметры модели, минимизируя расхождения между теоретическими и эмпирическими моментами данных. Байесовские методы оценки позволяют учесть априорные знания о значениях параметров модели и получить более точные оценки.
Критика и переосмысление: Наследие Хаавельмо в контексте современных дебатов об эконометрической методологии
Несмотря на огромный вклад Трюгве Хаавельмо в эконометрику, его работы не избежали критики и переосмысления в контексте современных дебатов об эконометрической методологии. Критика направлена на различные аспекты его подхода, включая предпосылки о рациональности экономических агентов, акцент на математической формализации и игнорирование контекстуальных факторов. Переосмысление наследия Хаавельмо происходит в рамках более широкого движения за более реалистичную, контекстуально-чувствительную и плюралистическую эконометрику. Это движение подчеркивает важность использования различных методов и подходов, а также учета социальных, политических и институциональных факторов, которые могут влиять на экономические явления.
Одним из основных пунктов критики является предпосылка о рациональности экономических агентов, которая лежит в основе многих эконометрических моделей, вдохновленных работами Хаавельмо. Критики утверждают, что эта предпосылка является нереалистичной и не учитывает когнитивные ограничения, эмоции и социальные влияния, которые могут влиять на поведение экономических агентов. Альтернативные подходы, такие как поведенческая экономика, предлагают более реалистичные модели поведения, которые учитывают эти факторы. Однако, включение поведенческих факторов в эконометрические модели может быть сложным, поскольку требует разработки новых методов и инструментов.
Другой пункт критики связан с акцентом Хаавельмо на математической формализации. Критики утверждают, что чрезмерная математизация может приводить к игнорированию содержательных аспектов экономических явлений и к упрощению сложных социальных процессов. Они подчеркивают важность использования качественных методов, таких как интервью и этнографические исследования, для получения более глубокого понимания экономических явлений. Однако, качественные методы также имеют свои ограничения, такие как субъективность и сложность обобщения результатов.
Кроме того, критике подвергается игнорирование контекстуальных факторов в эконометрических моделях. Критики утверждают, что экономические явления не происходят в вакууме, а зависят от конкретных социальных, политических и институциональных условий. Поэтому, эконометрические модели должны учитывать эти контекстуальные факторы, чтобы быть релевантными и полезными. Однако, включение контекстуальных факторов в модели может быть сложным, поскольку требует сбора и анализа большого количества информации.
Переосмысление наследия Хаавельмо происходит в рамках более широкого движения за более плюралистическую эконометрику. Плюрализм в эконометрике означает использование различных методов и подходов, а также признание легитимности различных точек зрения. Плюралистическая эконометрика признает, что не существует единого “правильного” способа анализа экономических явлений, и что различные методы и подходы могут быть полезны в разных контекстах. Плюрализм также означает учет социальных, политических и институциональных факторов, которые могут влиять на экономические явления.
Современные дебаты об эконометрической методологии также включают дискуссии о роли ценностей и идеологии в эконометрических исследованиях. Критики утверждают, что эконометрические исследования не являются нейтральными, а отражают ценности и идеологию исследователей. Поэтому, важно осознавать собственные ценности и идеологические предубеждения и учитывать их при проведении эконометрических исследований.
В заключение, наследие Трюгве Хаавельмо является предметом критики и переосмысления в контексте современных дебатов об эконометрической методологии. Критика направлена на предпосылки о рациональности, акцент на математической формализации и игнорирование контекстуальных факторов. Переосмысление наследия Хаавельмо происходит в рамках более широкого движения за более реалистичную, контекстуально-чувствительную и плюралистическую эконометрику. Несмотря на критику, вклад Хаавельмо в эконометрику остается огромным и неоспоримым. Его работы заложили основы для современной эконометрики и продолжают вдохновлять экономистов и эконометристов во всем мире. Современные дебаты об эконометрической методологии позволяют лучше понять сильные и слабые стороны подхода Хаавельмо и разрабатывать более совершенные методы анализа экономических явлений.
Важно помнить, что эконометрика является не только наукой, но и искусством. Она требует от исследователя не только знаний математики и статистики, но и интуиции, креативности и способности критически мыслить. Эконометрические модели являются лишь инструментами, которые помогают нам понимать экономический мир, но они не являются заменой здравого смысла и критического мышления.
Проверено на следующих конфигурациях и релизах:
- 1С:ERP Управление предприятием 2, релизы 2.5.20.85
Вступайте в нашу телеграмм-группу Инфостарт