Теоретических основ представленных алгоритмов в этой статье также не будет. Тех, кого этот момент заинтересовал, отсылаю к соответствующей литературе по вычислительным методам (практически в любой книге с разной степенью точности и понятности есть этот материал) или к Википедии. Как и в любых численных методах, следует уделять внимание вопросам выбора узлов и шага, начального приближения, обеспечения требуемой точности вычислений, а также применимости и целесообразности выбора того или другого метода.
Итак, рассмотрим задачу оптимизации на отрезке [2;7] функции: F(x) = sin(x) + 1/x
Функция Функция_3(х)
Возврат Окр(sin(х)+(1/х), 10);
КонецФункции
Вызов расчетных функций:
Процедура ВыполнитьРасчет()
Х_нач = 4;
Шаг = 0.001*Х_нач;
Точность = 0.0001*Х_нач;
Сообщить("Метод парабол = " + РассчитатьМетодомПарабол(Х_нач, Шаг, Точность));
Х_нач = 2;
Х_кон = 7;
Точность = 0.00001;
Сообщить("Метод золотого сечения = " + РассчитатьМетодомЗолотогоСечения(Х_нач, Х_кон, Точность));
КонецПроцедуры
Обратите внимание, что в методе парабол точность и шаг сделаны как функции от начального приближения.
Метод парабол:
Функция РассчитатьМетодомПарабол(Х_нач, Шаг, Точность)
Хц = Х_нач;
Флаг = Истина;
Пока Флаг = Истина Цикл
Хл = Хц - Шаг;
Хп = Хц + Шаг;
Хмин = 0.5*((Функция_3(Хл)*(Хп+Хц) - 2*Функция_3(Хц)*(Хп+Хл) + Функция_3(Хп)*(Хц+Хл)))
/(Функция_3(Хл)-2*Функция_3(Хц)+Функция_3(Хп));
Если МодульМ(Хмин-Хц) < Точность Тогда
Прервать;
КонецЕсли;
Хц = Хмин;
КонецЦикла;
Возврат Окр(Хмин, 10);
КонецФункции
Метод золотого сечения:
Функция РассчитатьМетодомЗолотогоСечения(a, b, Точность)
K = 1.618; // 0.5*(1 + Pow(5, 0.5));
Флаг = Истина;
Пока Флаг = Истина Цикл
Хл = b - (b-a)/K;
Хп = a + (b-a)/K;
Если Функция_3(Хл) >= Функция_3(Хп) Тогда
a = Хл;
Иначе
b = Хп;
КонецЕсли;
Если МодульМ(b-a) < Точность Тогда
Прервать;
КонецЕсли;
КонецЦикла;
Возврат Окр(0.5*(a+b), 10);
КонецФункции
Вспомогательная функция получения модуля:
Функция МодульМ(Числ)
Если Числ<0 Тогда
Возврат (Числ * (-1));
Иначе
Возврат (Числ);
КонецЕсли;
КонецФункции
Результат вычислений:
Метод парабол = 4,7566019087
Метод золотого сечения = 4,7566045089
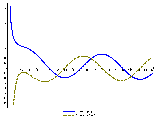
P.S. В картинках к публикации есть изображение графика рассмотренной функции (синяя сплошная линия), а также графика её производной (пунктирная зеленоватая линия). Видно, что на рассматриваемом участке наша функция достигает локального экстремума как раз примерно в той точке, значения которой были вычислены.