1. Задача
Суть решаемой задачи заключается в следующем:
Имеются вопросы теста 1С: Профессионал, поделенные, как правило, на 14 разделов. В каждом разделе заключено конкретное количество различных вопросов. На каждый вопрос имеется 5 (для определенности) вариантов ответов, один из которых является правильным. Прохождение теста заключается в выборе одного варианта ответа на каждый из 14 вопросов. Вопросы для каждого теста выбираются случайным образом - по одному из каждого раздела. По окончании прохождения теста испытуемому сообщается только количество правильных ответов. Какие именно ответы были правильными, не раскрывается. Требуется построить алгоритм, позволяющий определить правильные ответы на все вопросы тестов путем многократного прохождения теста методом проб и ошибок без какого-либо анализа сути вопросов.
2. Немного теории
В основе байесовской модели лежит понятие распределения вероятностей. Оно определяет вероятность каждого из возможных исходов некоторого "случайного" события. Например, бросание игрального кубика характеризуется распределением вероятностей (1/6, 1/6, 1/6, 1/6, 1/6, 1/6), а правильность выбранного "вслепую" варианта ответа описывается распределением (1/5, 1/5, 1/5, 1/5, 1/5). Исходное распределение вероятностей, называемое априорным, может впоследствии уточняться при поступлении дополнительной информации о событии. Например, если стало известно, что число, выпавшее при бросании кубика, четное, то уточненным распределением вероятностей будет распределение вероятностей (0, 1/3, 0, 1/3, 0, 1/3). Уточненное распределение вероятностей называется апостериорным, а процесс расчета апостериорного распределения на основе дополнительной информации и на основе априорного распределения называется байесовским выводом. Вывод производится на основе формулы условной вероятности или формулы Байеса:
Р( А | Б) = Р( АБ ) / Р( Б ) = Р( Б | А ) Р( А ) / Р( Б ),
где А - исследуемое событие, Б - зависимое событие, которое оказывается произошедшим в свете полученной дополнительной информации.
В одной этой формуле и заключается вся суть байесовской модели.
В следующий раз апостериорное распределение, полученное на предыдущем шаге, считается уже априорным и с получением следующей порции информации оно опять пересчитывается. До тех пор пока не будет достигнута максимальная определенность, например, распределение вероятностей не выродится в единичный вектор вида ( ..., 0, 1, 0, ...), что означает, что вероятен один единственный исход исследуемого события.
Мера неопределенности по ходу обучения может оцениваться формулой для расчета энтропии:
Σj = 1,n | - Pj log(Pj) |
В процессе обучения эта мера должна снижаться, что характеризует прогресс обучения.
3. Алгоритм решения
В рассматриваемой задаче исходная неопределенная ситуация характеризуется распределениями вероятностей правильности каждого варианта ответа на каждый из вопросов. Первоначально все варианты ответа на каждый вопрос считаются равновероятно правильными, а неопределенность максимальна.
Количество правильных ответов K пройденного теста (событие Б) естественно зависит от того, какие ответы были выбраны и какова была вероятность, что они правильные. Если число К становится известно (событие Б произошло), то из априорных распределений легко рассчитать знаменатель в формуле Байеса (вероятность события Б). Это будет сумма вероятностей всех комбинаций ответов, в которых К вопросов выбрано правильно, а (14 - К) - неправильно. Числителем для каждого вопроса пройденного теста будет сумма вероятностей тех комбинаций, в которых выбранный ответ на этот вопрос правильный (вероятность совместной реализации А и Б). Зная числитель и знаменатель, легко пересчитать апостериорную вероятность того, что выбранный вариант ответа на соответствующий вопрос действительно правильный. Вероятности для оставшихся вариантов ответов пересчитываются пропорционально их старым значениям с учетом условия равенства суммы вероятностей единице.
В итоге алгоритм решения заключается в последовательном прохождении тестов, в каждом из которых на основе априорных вероятностей выбираются ответы на предложенные вопросы, а после получения информации о количестве правильных ответов пересчитываются распределения вероятностей правильности ответов по формуле Байеса. До тех пор пока полученные распределения вероятностей не станут однозначно определять правильные ответы.
4. Подробности реализации
Более конкретно на языке системы "1С: Предприятие" для работы алгоритма необходимо определить таблицу значений, число строк в которой равно общему числу имеющихся вопросов во всех разделах теста. Сами вопросы в таблице хранить не нужно, их содержание значения не имеет. Если возможно пять вариантов ответа, то в таблице нужно завести пять колонок с именами Р1 - Р5 числового типа достаточной точности для представления вероятностей. Например, типа Число(10, 9). Первоначально все ответы равновероятны, поэтому все колонки заполняются значением 0,2 (= 1 / 5). Также в таблице заводится колонка "НомерТеста" для отметки вопросов текущего теста, колонка номера выбранного ответа и служебная колонка "Числитель" для расчета числителя формулы Байеса. В результате прохождения теста соответствующие строки отмечаются номером текущего теста, заполняется номер выбранного ответа, а также становится известным число правильных ответов.
Для выбора варианта ответа и пересчета вероятностей Р1 - Р5 в выбранных по номеру текущего теста строках таблицы используется следующая процедура:
Процедура Тестирование(ПараметрыТестирования)
ГСЧ = Новый ГенераторСлучайныхЧисел();
ПравильныхОтветов = 0;
Код = "";
Для НомерВопроса = 0 По Отчет.ЧислоВопросовТеста - 1 Цикл
НомерВарианта = ГСЧ.СлучайноеЧисло(0, Отчет.ЧислоВариантовОдногоВопроса - 1);
ВопросТеста = Отчет. Вопросы[НомерВопроса * Отчет.ЧислоВариантовОдногоВопроса + НомерВарианта];
ВопросТеста.НомерТеста = ПараметрыТестирования.НомерТеста;
ВопросТеста.ВыбранныйОтвет = ВыборПоВероятности(ВопросТеста, ГСЧ);
ВопросТеста.Числитель = 0;
ПравильныхОтветов = ПравильныхОтветов + (ВопросТеста.ВыбранныйОтвет = ВопросТеста.ПравильныйОтвет); //только для подсчета!!!
Код = "0" + Код + "1"
КонецЦикла;
ПараметрыТестирования.ЧислоПравильныхОтветов = ПравильныхОтветов;
Знаменатель = 0;
Код = Сред(Код, ПравильныхОтветов + 1, Отчет.ЧислоВопросовТеста); // инициализация перебора комбинаций расположения правильных ответов
ВопросыТеста = Отчет.Вопросы.НайтиСтроки(Новый Структура("НомерТеста", ПараметрыТестирования.НомерТеста));
Пока СтрЧислоВхождений(Код, "1") = ПравильныхОтветов Цикл // перебор комбинаций
ВероятностьКомбинации = 1;
Для Сч = 0 По Отчет.ЧислоВопросовТеста - 1 Цикл
ВероятностьПравильностиОтвета = ВопросыТеста[Сч]["Р" + ВопросыТеста[Сч].ВыбранныйОтвет];
ВероятностьКомбинации = ВероятностьКомбинации * ?(Сред(Код, Сч + 1, 1) = "1", ВероятностьПравильностиОтвета, 1 - ВероятностьПравильностиОтвета)
КонецЦикла;
Для Сч = 0 По Отчет.ЧислоВопросовТеста - 1 Цикл
ВопросыТеста[Сч].Числитель = ВопросыТеста[Сч].Числитель + ?(Сред(Код, Сч + 1, 1) = "1", ВероятностьКомбинации, 0)
КонецЦикла;
Знаменатель = Знаменатель + ВероятностьКомбинации;
Код = СледующийКод(Код)
КонецЦикла;
Для Каждого Вопрос ИЗ ВопросыТеста Цикл // пересчет вероятностей
ЭнтропияДо = Энтропия(Вопрос);
УсловнаяВероятность = Вопрос.Числитель / Знаменатель;
БылаВероятность = Вопрос["Р" + Вопрос.ВыбранныйОтвет];
Если БылаВероятность = 1 Тогда
ПараметрыТестирования.Энтропия = ПараметрыТестирования.Энтропия + 0 - ЭнтропияДо;
Продолжить
КонецЕсли;
Вопрос["Р" + Вопрос.ВыбранныйОтвет] = 1;
Для Ответ = 1 По Отчет.ЧислоВариантовОтвета Цикл
Если Ответ <> Вопрос.ВыбранныйОтвет Тогда
Вопрос["Р" + Ответ] = Вопрос["Р" + Ответ] * (1 - УсловнаяВероятность) / (1 - БылаВероятность);
Вопрос["Р" + Вопрос.ВыбранныйОтвет] = Вопрос["Р" + Вопрос.ВыбранныйОтвет] - Вопрос["Р" + Ответ]
КонецЕсли
КонецЦикла;
ПараметрыТестирования.Энтропия = ПараметрыТестирования.Энтропия + Энтропия(Вопрос) - ЭнтропияДо;
КонецЦикла
КонецПроцедуры
В качестве вспомогательной здесь используется функция генерации всех возможных строк из "0" и "1" заданной длины в порядке увеличения количества "1". Задав в качестве начального кода строку вида "000...111", содержащую число единиц, соответствующую числу правильных ответов, можно получить все комбинации расположения правильных ответов в тесте.
Функция СледующийКод(Код)
Возврат Прав(СтрЗаменить(Код, "1", "0") + Лев("1" + Код, Найти(Код, "0"))
+ ?(Найти(Код, "01"), "0", "") + Сред(Код, Найти(Код + "01", "01") + 2), СтрДлина(Код))
КонецФункции
Для четырех знаков эта простая функция порождает последовательность "0000", "0001", "0010", "0100", "1000", "0011", "0101", "1001", "0110", "1010", "1100", "0111", "1011", "1101", "1110", "1111", "0000" и так далее.
5. Практическая проверка
К статье приложена обработка "Угадайка правильных ответов теста" для испытания алгоритма. В обработке можно задать число вопросов теста, число различных вопросов в разделе, число возможных ответов на один вопрос. Случайным образом генерируется номер правильного ответа на каждый вопрос. Обработка не обращается напрямую к этой информации, а получает только количество правильных ответов. При этом обработка шаг за шагом сужает неопределенность в отношении правильности разных вариантов ответов и в конечном итоге определяет правильные ответы на все вопросы в соответствии с предложенным алгоритмом. Это можно увидеть на Фиг.1 для задачи небольшой размерности с параметрами: 6 вопросов по два варианта в разделе и пять вариантов ответа на каждый вопрос.
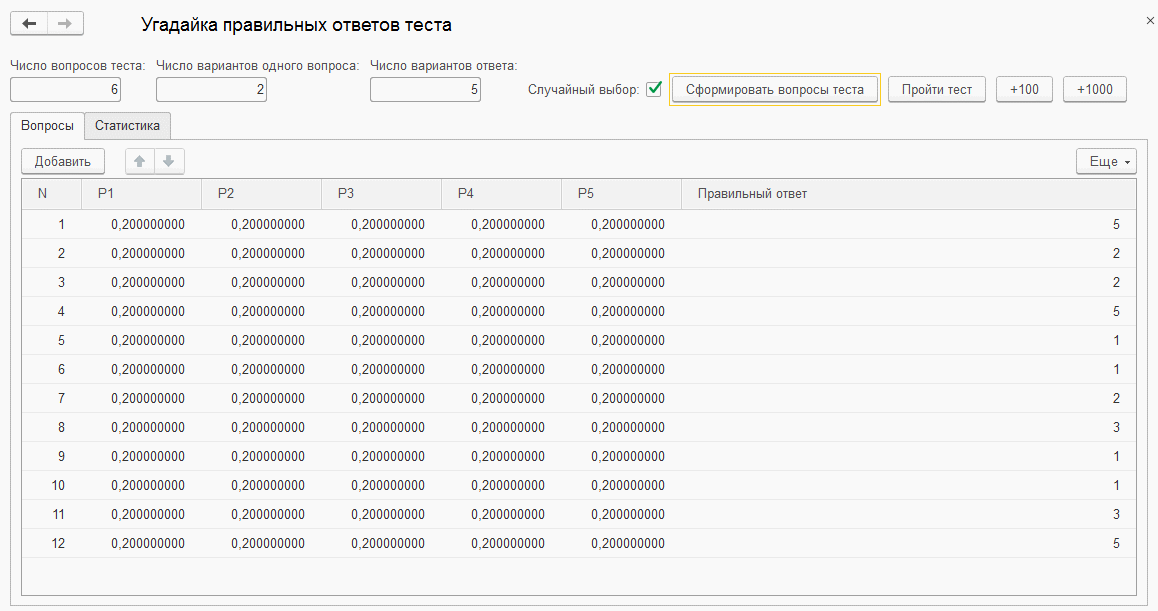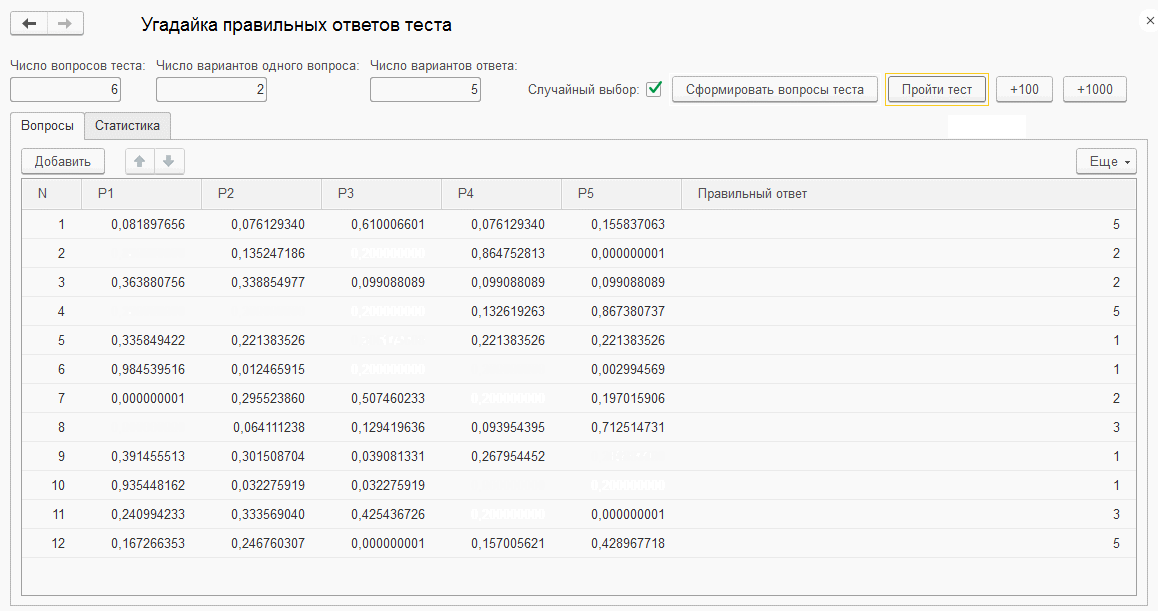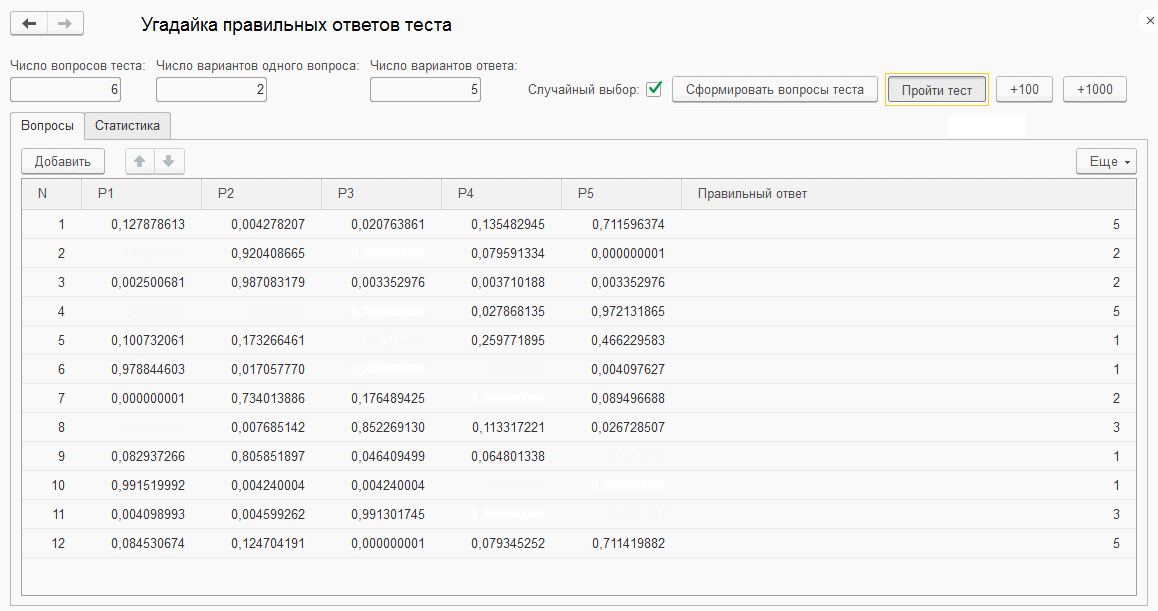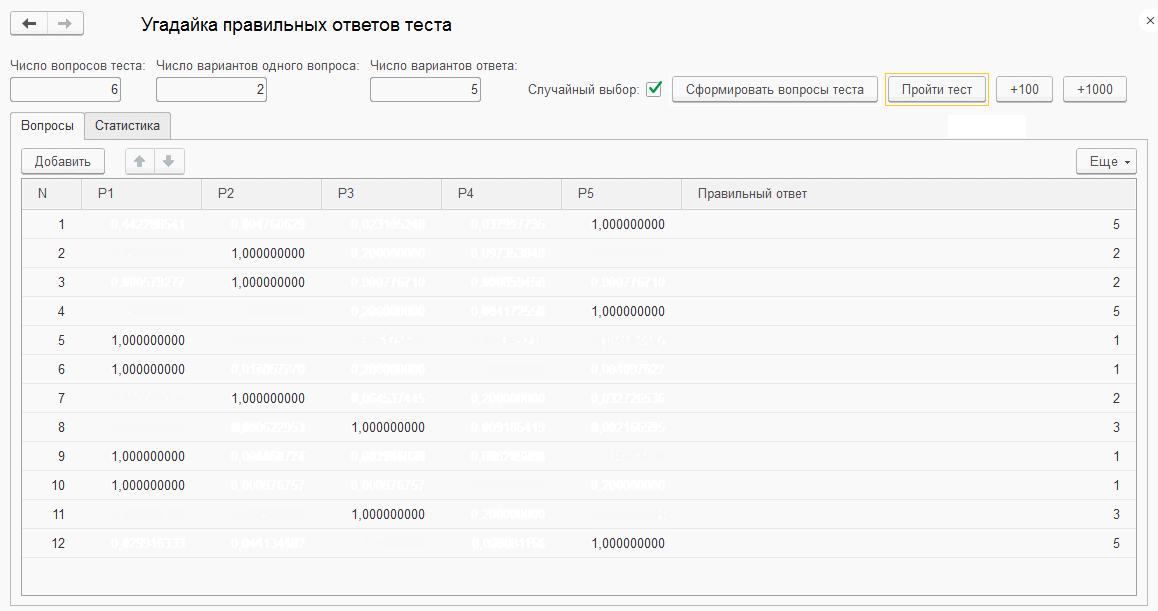
Для 14-ти вопросов, 50 вопросов в каждом разделе, 5-ти вариантах ответов обработке необходимо примерно 2500 прохождений теста для завершения обучения. Это не так уж много, учитывая, что в конечном итоге определяются правильные ответы на каждый из 700 вопросов теста с пятью вариантами ответов на каждый вопрос.
На Фиг.2 изображен постепенный рост количества правильных ответов в обработке по мере прохождения обучения.
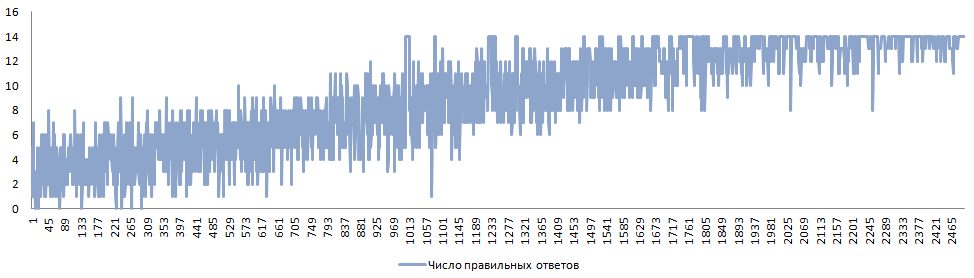
На Фиг.3 изображено соответствующее постоянное и равномерное снижение энтропии в определенности правильности разных вариантов ответов на вопросы по мере обучения.
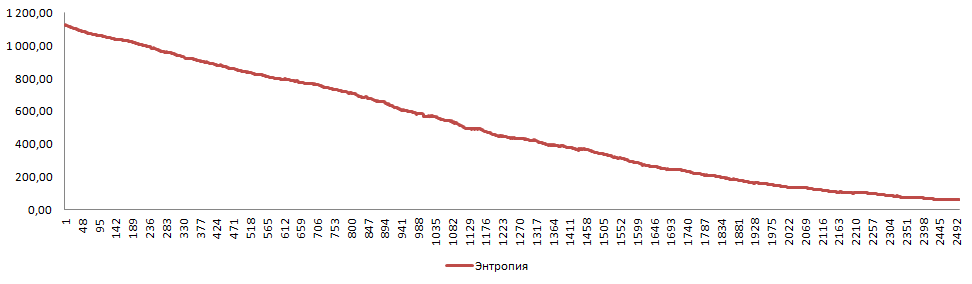
Отдельно стоит сказать о стратегии выбора ответов в тесте. Ответы в предложенной обработке выбираются случайным образом пропорционально априорным вероятностям (есть галочка в настройках). То есть используется рандомизированная стратегия. Выбор ответа по максимальной вероятности оказывается немного хуже, особенно на финальной стадии, когда ответы на многие вопросы уже известны.
6. Выводы
Как видно, байесовская модель точно подошла к решаемой задаче и позволила получить решение с минимальными затратами времени и других вычислительных ресурсов.
Это значит, что несмотря на то, что сейчас внимание исследователей и заинтересованной общественности приковано в основном к нейронным сетям, последние не всегда являются "серебряной пулей", а классические модели еще рано выкидывать на свалку. Тем более, что ажиотаж вокруг нейронных сетей может закончится так же внезапно, как начался, с исчерпанием круга решаемых ими задач [ ссылка ]. Кстати, нейросетевые модели прекрасно комбинируются с байесовским выводом в нейробайесовских моделях, пропагандируемых, например, Ветровым [ ссылка ].
Эта замечательная задача была придумана Максимом Б (Xershi) и предложена им в ходе обсуждения реальных практических задач для нейронных сетей. Решение, найденное в ходе обсуждения, показалось настолько поучительным, что была высказана просьба и получено согласие использовать эту задачу для публикации найденного решения.