Об игре
История Game of Life началась даже не с Джона Конвея, а с Джона фон Неймана - основоположника сегодняшней компьютерной архитектуры (архитектура фон Неймана, в противоположность гарвардской архитектуре). В процессе доказательства существования самовоспроизводящихся машин он смоделировал автомат, работающий на клеточной доске. Радикально упростив этот автомат, Джон Конвей получил набор правил, которые и стали основой для игры "Жизнь".
Правила из Википедии:
- Место действия игры — размеченная на клетки плоскость, которая может быть безграничной, ограниченной или замкнутой.
- Каждая клетка на этой поверхности имеет восемь соседей (окрестность Мура), окружающих её, и может находиться в двух состояниях: быть «живой» (заполненной) или «мёртвой» (пустой).
- Распределение живых клеток в начале игры называется первым поколением. Каждое следующее поколение рассчитывается на основе предыдущего по таким правилам:
- в пустой (мёртвой) клетке, с которой соседствуют три живые клетки, зарождается жизнь;
- если у живой клетки есть две или три живые соседки, то эта клетка продолжает жить; в противном случае (если живых соседей меньше двух или больше трёх) клетка умирает («от одиночества» или «от перенаселённости»).
- Игра прекращается, если
- на поле не останется ни одной «живой» клетки;
- конфигурация на очередном шаге в точности (без сдвигов и поворотов) повторит себя же на одном из более ранних шагов (складывается периодическая конфигурация)
- при очередном шаге ни одна из клеток не меняет своего состояния (частный случай предыдущего правила, складывается стабильная конфигурация)
Несмотря на достаточно простые правила, существует великое множество интересных конфигураций, возникающих в процессе игры:
- Устойчивые фигуры: фигуры, которые остаются неизменными
- Долгожители: фигуры, которые долго меняются, прежде чем стабилизироваться;
- Периодические фигуры: фигуры, у которых состояние повторяется через некоторое число поколений, большее 1;
- Двигающиеся фигуры: фигуры, у которых состояние повторяется, но с некоторым смещением;
- Ружья: фигуры с повторяющимися состояниями, дополнительно создающие движущиеся фигуры;
- Паровозы: двигающиеся фигуры с повторяющимися состояниями, которые оставляют за собой другие фигуры в качестве следов;
- Пожиратели: устойчивые фигуры, которые могут пережить столкновения с некоторыми двигающимися фигурами, уничтожив их;
- Отражатели: устойчивые или периодические фигуры, способные при столкновении с ними движущихся фигур поменять их направление;
- Размножители: конфигурации, количество живых клеток в которых растёт как квадрат количества шагов;
Очевидно, что максимальная скорость распространения популяции - 1 клетка за 1 ход (по горизонтали, вертикали или диагонали). Логично, что она получила название скорость света.
Удивительно, но игра имеет отношение к самым разным наукам: квантовой физике, электротехнике, химии, даже биологии - у некоторых ящериц окраска чешуек формируется по похожим принципам.
Нельзя не упомянуть об эмблеме хакеров, содержащей в себе планер - двигающуюся фигуру.
Эта фигура за каждые 4 хода смещается на 1 клетку по диагонали. Таким образом планер двигается со скоростью 1/4 скорости света.
С помощью планеров можно конструировать счётчики, логические вентили И, ИЛИ, НЕ. С использованием планеров можно доказать, что «Жизнь» в качестве вычислительной машины является полной по Тьюрингу.
О реализации
Первая проблема, с которой сталкивается любой, кто собрался реализовать эту игру - поле. Так как прямоугольное поле имеет границы, то как должна развиваться колония клеток на границе? Есть два подхода - первый: считать, что за границей поля нет и не может быть живых клеток, и второй: соединить противоположные края, превратив прямоугольник в тор. Обычно используется второй вариант - планер, вылетев за нижний край, вернется сверху.
Основных подходов к реализации алгоритмов тоже два.
Первый подход заключается в создании двумерного массива по размеру поля, элемент массива соответствует клетке поля. Автор этих строк когда-то использовал в качестве такого массива видеопамять VGA. Очевидно, что а) при таком подходе поле ограничено доступной памятью, б) алгоритм игры содержит обход по двумерному массиву, его производительность значительно падает при увеличении поля, в) обычно скорость выполнения почти не зависит от заполненности поля. Второй подход вместо массива для поля предполагает массив для клеток. Элемент массива содержит координаты клетки. Потенциально с помощью такого подхода можно иметь в игре "бесконечное" поле. Но в этом случае а) скорость и объем необходимой памяти зависит от количества клеток в популяции, б) появляется проблема быстрого поиска клеток по координатам.
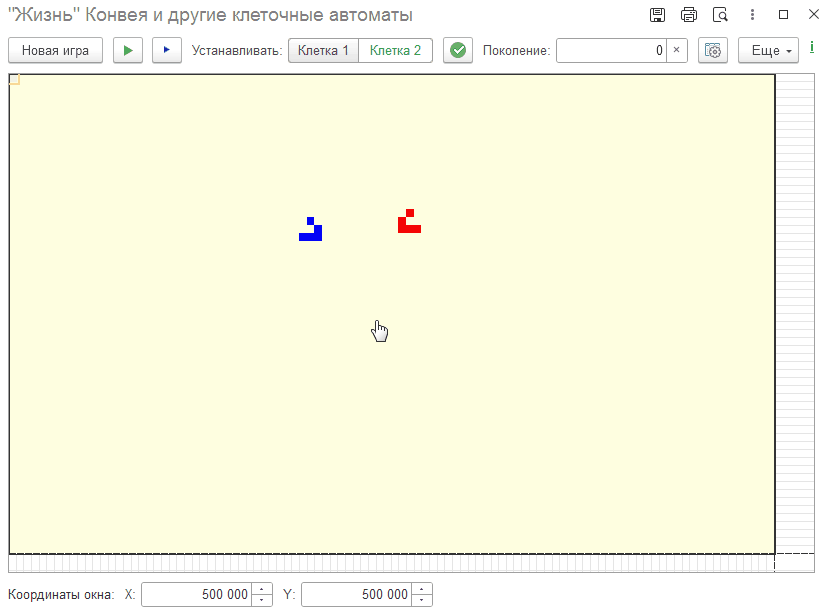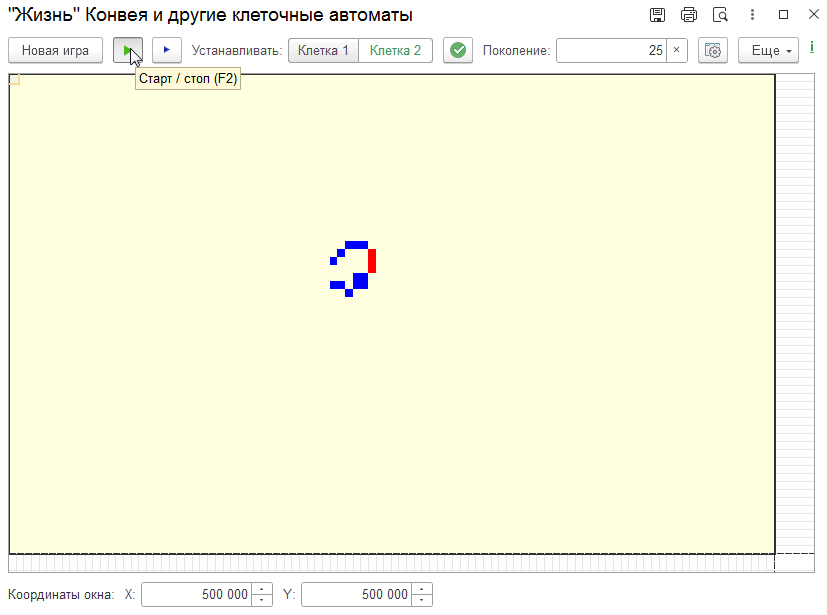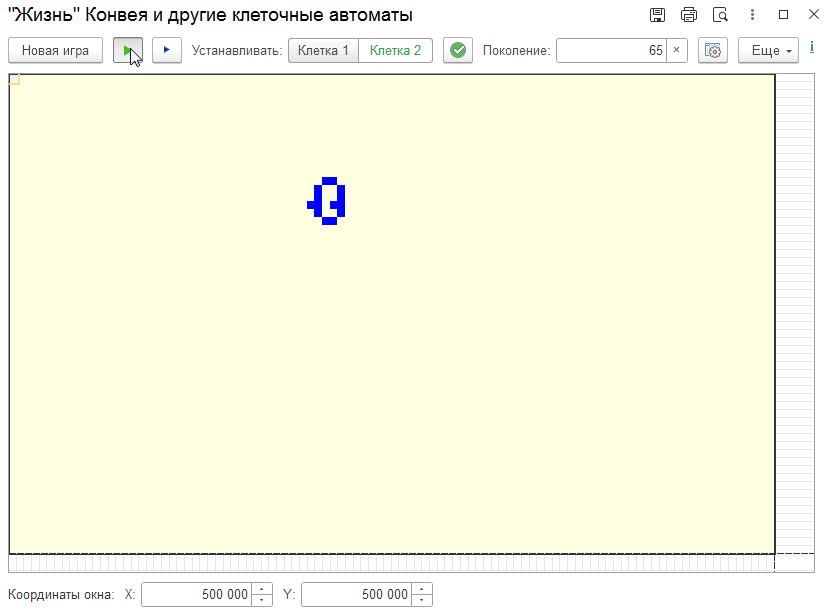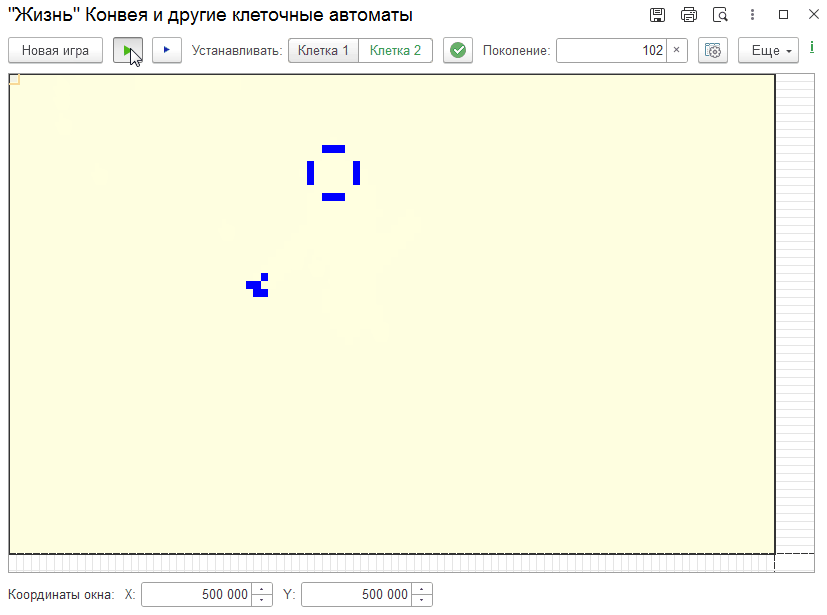
В предлагаемой реализации игры используется второй подход, для хранения клеток используется Соответствие, ключом которого являются координаты клетки. Потенциальный размер поля - 1000000*1000000. На экране видима только часть поля - окно, которое можно "перемещать" по полю.
Еще один интересный алгоритм на основе запроса описан в Игра "Жизнь" в одном запросе.
Аналогов игры в интернете полно, в том числе и на Инфостарте: раз, два, три ... Но игры на основе клеточных автоматов не ограничиваются указанными выше правилами. А что если изменить количество соседей?
Другие клеточные автоматы
Предположим, что новая клетка рождается (birth) если у нее 3 соседа, а выживает (survival) если имеет 2 или 3 соседей. Тогда правила для игры "жизнь" описываются формулой B3/S23. Меняя в этой формуле цифры, мы получим другие правила и другие игры, со своими закономерностями и интересными эффектами.
День и ночь (B3678 / S34678)
Есть интересная особенность: поле можно "инвертировать", тогда конфигурация "мертвых" клеток будет вести себя так же, как и бывшая конфигурация "живых клеток".
Жизнь без смерти (B3 / S012345678)
Здесь клетки вообще не умирают, их количество постоянно увеличивается, порождая разнообразные узоры, часто симметричные или периодические.
HighLife (B36 / S23)
Во многом похожа на "Жизнь". Здесь интересен репликатор - конфигурация клеток которая создает свои копии по обеим сторонам, эти копии - свои копии, которые сталкиваются, уничтожаются, после чего остаются два экземпляра удаляющиеся друг от друга.
Семена (B2 / S)
Здесь ни одна из клеток не выживает, но перед смертью может дать жизнь новой клетке. Интересно наличие фотонов, движущихся со скоростью света. Сталкиваясь, фотоны могут погибнуть, а могут породить другие фотоны (чем не физика элементарных частиц!))).
Morley (B368 / S245)
Эта игра примечательна наличием простого паровоза, двигающейся фигуры, оставляющей за собой дым. За 170 шагов он перемещается на 13 клеток
В прилагаемой к статье игре пользователь может выбрать любую игру из вышеуказанного списка, или создать игру по своим правилам.
Прочие виды правил перечислены здесь, и здесь, а еще здесь.
Игра тестировалась в тонком клиенте 8.3.22.1709.
Как всегда, приветствуются замечания / дополнения / комментарии.
Вступайте в нашу телеграмм-группу Инфостарт