Для примера возьму ситуацию из своей практики (что и послужило поводом для изучения вариантов решения данного вопроса), чтоб был максимально приближен к жизни.
Исходные данные:
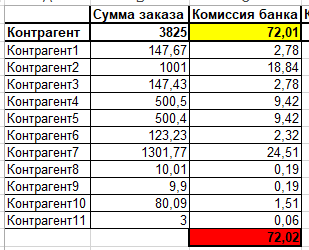
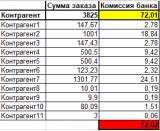
1. Есть платеж интернет эквайринга (заказ) на сумму 3825 руб., который в свою очередь на сайте складывается из определенных сумм, принадлежащих разным контрагентам, к примеру когда вы покупаете одним заказом на маркетплэйсе товар который по факту принадлежит разным продавцам.
2. За данную транзакцию банк взял комиссию в размере 72,01
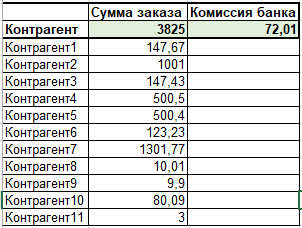
Задача заключается в распределении (удержании) комиссии банка с контрагента
Варианты решения:
1. Многие, в том числе и я до сие поры), сказал бы что надо просто распределить пропорционально суммам (наивный алгоритм), давайте попробуем.
Получаем следующую картину, здесь мы строку заказа/сумму заказа*сумму комиссии и применили математические правила округления
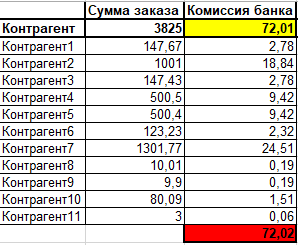
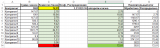
Как мы видим, что итоговая сумма распределения получилась больше на одну копейку.
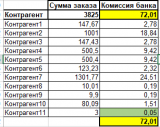
Хм... и это не проблема сказали мы, просто учтем разницу в определенной строке, к примеру в последней.
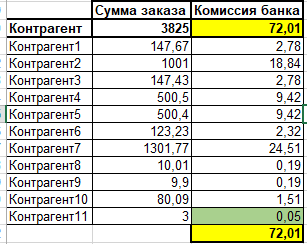
По цифрам вроде все красиво, задача решена, а решена ли?
Давайте посмотрим со стороны бизнеса и взаиморасчетов с клиентами.
Получается мы просто необоснованно уменьшили сумм удержания с контрагента11, она ведь стала меньше, ему еще и лучше скажете вы)), но разница может быть как в большую так и в меньшую сторону, и это только один заказ, а таких заказов ежедневно тысячи, а в год?.
Мы ведь с вами занимаемся учетом, зайдите в бухгалтерию и скажите что копейка это не важно, что они вам ответят?
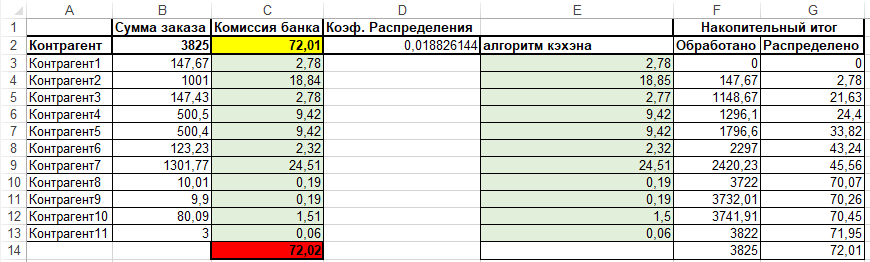
2. Алгоритм Кэхэна
суть алгоритма можно почитать в википедии, а также в телеграмм канале "Радио 1С Энтерпрайз" где я и услышал первый раз (думаю я не один) о существовании этого алгоритма, если в двух словах то мы вводим дополнительную переменную для накопления распределенной суммы, и вносим правки на округление при каждой итерации.
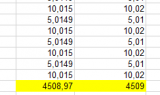
Получаем:
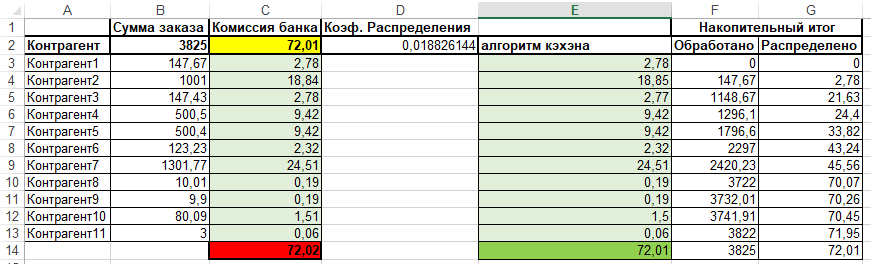
Сама формула в эксель выглядит следующим образом
=ОКРУГЛ(((B3+F3)*$D$2)-G3;2)
Важно отметить что порядок распределения сумм зависит от порядка записей, чтоб нам обеспечить неизменность распределения при каждой попытке, порядок всегда должен быть идентичен.
Чтоб было привычно и не чуждо 1сному глазу, приведу пример процедуры.
Процедура АлгоритРаспределенияКэхэна(МассивЗначений, СуммаЗаказа, СуммаКомиссии)
ОбработаноЗаписейНакопительно = 0;
РаспределеноЗаписейНакопительно = 0;
КоэфРаспределения = СуммаКомиссии/СуммаЗаказа;
Для каждого ЭлементМассива ИЗ МассивЗначений Цикл
СуммаРаспределения = ОКР(ЭлементМассива+ОбработаноЗаписейНакопительно)*КоэфРаспределения-РаспределеноЗаписейНакопительно,2);
ОбработаноЗаписейНакопительно = ОбработаноЗаписейНакопительно+ЭлементМассива;
РаспределеноЗаписейНакопительно = РаспределеноЗаписейНакопительно+ СуммаРаспределения;
КонецЦикла;
КонецПроцедуры
Данное решение получается более правильным с точки зрения математических правил, а также более устойчивое к входным данным и конечно более правильным со стороны учета.
Многие, может, давно применяют такой алгоритм, просто не знали, что он так красиво называется, лично для себя я положил его в копилку новых знаний.
Ремарка после прочтения комментариев.
Разница в одну копейку в данном примере не так выразительна, и при такой вводной не так однозначно преимущество второго алгоритма и недостатки первого, на последнею запись или по весу.
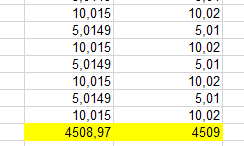
В данном примере у меня около полутысячи строк, и уже выходим на более ощутимую разницу, и любой подход распределения после всех итераций будет не оптимальным.
Так или иначе мы в любом случае не уйдем от того что эту копейку нужно куда то пристроить, и лучше это сделать в текущей итерации, к примеру по приведенному алгоритму Кэхэна, чем разницу в распределять к конце, которая может быть далеко не в копейку, и распределение на конкретную запись, пусть даже по весу будет еще более неправильной.